فاصله

فاصِله یک کمیت عددی برای تعیین مقدار دوری یا نزدیکی دو چیز است.

«فاصله» در زمینه‌های مختلفی تعریف می‌شود. به عنوان مثال، فاصلهٔ دو جسم از هم یا فاصلهٔ دو روز از سال.

در هندسه

در هندسهٔ اقلیدسی، انواع مختلفی از فاصله تعریف می‌شود؛ امّا به طور کلّی منظور از «فاصله» همان فاصلهٔ اقلیدسی است.

فاصلهٔ اقلیدسی

به طول کوتاه‌ترین خط بین دو نقطه‌ی ${\displaystyle A}$ و ${\displaystyle B}$ فاصلهٔ اقلیدسی (با نماد ${\displaystyle {\overline {AB}}}$[1]) گفته می‌شود.

در هندسهٔ تحلیلی فاصلهٔ بین دو نقطه‌ی ${\displaystyle A=(A_{x},A_{y})}$ و ${\displaystyle B=(B_{x},B_{y})}$ را می‌توان به کمک قضیهٔ فیثاغورث پیدا کرد که به فرمول زیر می‌رسد[2]:

${\displaystyle {\overline {AB}}={\sqrt {\Delta x^{2}+\Delta y^{2}}}={\sqrt {(A_{x}-B_{x})^{2}+(A_{y}-B_{y})^{2}}}}$

این فرمول را می‌توان به ابعاد بالاتر تعمیم داد؛ یعنی اگر ${\displaystyle A=(A_{1},A_{2},\dots ,A_{n})}$ و ${\displaystyle B=(B_{1},B_{2},\dots ,B_{n})}$:

${\displaystyle {\overline {AB}}={\sqrt {\sum _{i=1}^{n}{(\Delta A_{i})^{2}}}}={\sqrt {(A_{1}-B_{1})^{2}+(A_{2}-B_{2})^{2}+\dots +(A_{n}-B_{n})^{2}}}}$

فاصله میان نقطه و خط

فاصله میان نقطه (${\displaystyle P=(x_{p},y_{p}}$ و خط ${\displaystyle l}$، از طریق نقاط ${\displaystyle (x_{0},y_{0})}$ و ${\displaystyle (x_{1},y_{1})}$ برابر است با:

${\displaystyle d(P,l)={\sqrt {(x_{p}-x_{0}-\lambda _{q}(x_{1}-x_{0}))^{2}+(y_{p}-y_{0}-\lambda _{q}(y_{1}-y_{0}))^{2}}}}$

که در آن:

${\displaystyle \lambda _{q}={\frac {(x_{1}-x_{0})(x_{p}-x_{0})+(y_{1}-y_{0})(y_{p}-y_{0})}{(x_{1}-x_{0})^{2}+(y_{1}-y_{0})^{2}}}}$

اگر مقدار ${\displaystyle \lambda _{q}}$ میان ۰ و ۱ باشد نقطهٔ تقاطع ${\displaystyle l}$ و خط گذرنده از ${\displaystyle P}$ و عمود بر ${\displaystyle l}$ بین نقاط ${\displaystyle (x_{0},y_{0})}$ و ${\displaystyle (x_{1},y_{1})}$ جای می‌گیرد.

فاصلهٔ منهتنی

در منهتن انتخاب بین مسیر‌های زرد و آبی و قرمز فرقی در مسافت طی‌شدهٔ نهایی ایجاد نمی‌کند

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

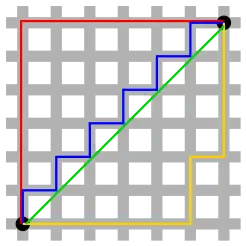
نام این نوع فاصله از منهتن در نیویورک آمریکا الهام گرفته شده؛ به این دلیل که نقشهٔ جادّه‌های آنجا بلوک‌بندی شده. فاصلهٔ منهتنی دو خانه برابر مسافتی ست که یک تاکسی باید طی کند تا به مقصد برسد.

فاصلهٔ منهتنی دو نقطه‌ی ${\displaystyle A=(A_{x},A_{y})}$ و ${\displaystyle B=(B_{x},B_{y})}$ (با نماد ${\displaystyle d_{1}}$) با فرمول زیر تعریف می‌شود:

${\displaystyle \mathrm {d_{1}} (A,B)=\left\vert \Delta x\right\vert +\left\vert \Delta y\right\vert }$

این فرمول را نیز می‌توان به ابعاد بالاتر تعمیم داد.

فاصلهٔ شطرنجی (فاصلهٔ چبیشف)

این نوع فاصله به این دلیل شطرنجی نامیده شده که در شطرنج برابر تعداد نوبت‌های مورد نیاز شاه برای رسیدن به مقصدش می‌باشد.

فاصلهٔ شطرنجی دو نقطه‌ی ${\displaystyle A=(A_{x},A_{y})}$ و ${\displaystyle B=(B_{x},B_{y})}$ (با نماد ${\displaystyle d_{1}}$) با فرمول زیر تعریف می‌شود:

${\displaystyle \mathrm {d_{\infty }} (A,B)=\max\{\Delta x,\Delta y\}}$

این فرمول را نیز می‌توان به ابعاد بالاتر تعمیم داد.

تعمیم و فاصلهٔ مینکوفسکی

در فضای ${\displaystyle \mathbb {R} ^{n}}$ فاصلهٔ مینکوفسکی از مرتبهٔ ${\displaystyle p}$ (یا p-نُرم با نماد ${\displaystyle \mathrm {d} _{p}}$) بین دو نقطه‌ی ${\displaystyle A=(A_{1},A_{2},\dots ,A_{n})}$ و ${\displaystyle B=(B_{1},B_{2},\dots ,B_{n})}$ به صورت زیر تعریف می‌شود:

${\displaystyle \left(\sum _{i=1}^{n}\left|A_{i}-B_{i}\right|^{p}\right)^{1/p}}$

فاصلهٔ منهتنی معادل ۱-نرم، فاصلهٔ شطرنجی معادل ∞-نرم و فاصلهٔ اقلیدسی معادل ۲-نرم (${\displaystyle \mathrm {d} _{2}}$) هستند.

در گراف

در نظریّهٔ گراف‌ها، فاصلهٔ دو رأس (با نماد ${\displaystyle d}$) برابر طول کوتاه‌ترین مسیر بین دو آن دو تعریف می‌شود[3].

منابع

1. سازمان بین‌المللی استانداردسازی (2019-08). "ISO 80000-2:2019 Quantities and units — Part 2: Mathematics". line feed character in |عنوان= at position 17 (help); Check date values in: |تاریخ انتشار= (help)
2. «۱۲٫۱». Thomas' Calculus (14th Edition).
3. «۲٫۱». Introduction to Graph Theory (2nd Edition). به کوشش Douglas B. West.

مجموعه‌ای از گفتاوردهای مربوط به فاصله در ویکی‌گفتاورد موجود است.