نمودار تنش-کرنش مهندسی

نمودار تنش-کرنش مهندسی معمول‌ترین نوع نمودار تنش-کرنش است که در آن مقادیر تنش و کرنش از ابعاد اولیهٔ (تغییر شکل نیافتهٔ) نمونه محاسبه می‌شوند.[1] از داده‌های این نمودار می‌توان استحکام تسلیم، مدول یانگ، استحکام نهایی و ازدیاد طول شکست را محاسبه کرد.[2] در اکثر جامدات (به استثنای برخی از پلیمرهای لاستیکی) بخش ابتدایی این منحنی خطی بوده و مربوط به تغییر شکل الاستیک برگشت‌پذیر است.[3] از آنجایی که در این مواد کاهش سطح مقطع در حین تغییر شکل الاستیک کمتر از ۱٪ است، این بخش از نمودار تنش-کرنش مهندسی مانند نمودار تنش-کرنش حقیقی است.[4] رفتار مواد تحت تنش کششی را می‌توان بر اساس شکل نمودار تنش-کرنش مهندسی آن‌ها طبقه‌بندی کرد:

رفتار الاستیک
نمودار تنش-کرنش شیشه

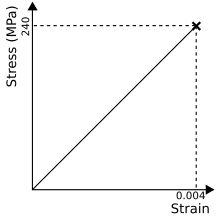
این نوع نمودار تنش-کرنش نشانگر رفتار کاملاً کشسان است. در این حالت ماده هیچ‌گونه تغییر شکل پلاستیکی از خود نشان نمی‌دهد و کاملاً از قانون هوک تبعیت می‌کند.[5][6]

که در اینصورت تنش () با کرنش () رابطهٔ خطی داشته و ضریب تناسب (E) مدول یانگ نامیده می‌شود. در هنگام باربرداری نیز این مواد کاملاً به حالت اولیهٔ خود بازمی‌گردند.[7] شیشه‌ها، سنگ‌ها، اکثر سرامیک‌ها و پلیمر‌های دارای پیوند عرضی زیاد رفتاری مانند این نمودار داشته و بدون تغییرشکل پلاستیک به صورت ترد می‌شکنند.[8]

رفتار ویسکوالاستیک
نمودار تنش-کرنش شماتیک رفتار
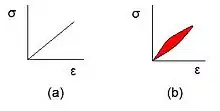
(a) الاستیک و
(b) ویسکوالاستیک

بیشتر مواد زیستی رفتار ویسکوالاستیک از خود نشان می‌دهند. این مواد پس از برداشته‌شدن بار به شکل اولیهٔ خود بازمی‌گردند اما فرایند بازگشت زمانبر بوده[9] و شیب منحنی باربرداری با بارگذاری یکسان نیست. مساحت ناحیهٔ محصور بین این دو منحنی انرژی تلف‌شده در حین این تغییر شکل است.[10]

رفتار الاستیک-پلاستیک یکنواخت
نمودار تنش-کرنش مهندسی آلومینیوم
۱-استحکام نهایی
۲-استحکام تسلیم
۳-حد تناسب
۴-شکست
۵-کرنش قراردادی تسلیم

وقتی ماده‌ای امکان تغییر شکل پلاستیک داشته‌باشد، منحنی تنش-کرنش مهندسی آن به صورت روبرو خواهد بود.[11] از آنجایی که این مواد نقطهٔ تسلیم مشخصی ندارند، از کرنش قرارداد تسلیم برای تعیین نقطهٔ تسلیم در آن‌ها استفاده می‌شود. حد تسلیم تنشی در نظر گرفته می‌شود که کرنش مومسانی برابر با کرنش قراردادی تسلیم ایجاد کند.

رفتار الاستیک-پلاستیک غیریکنواخت

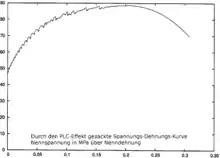
در برخی از مواد نمودار تنش-کرنش دندانه‌دار دارند.[12] این نوع نمودار نشان‌دهندهٔ تغییرات ساختاری ناهمگن در ماده است. جوانه‌زنی و رشد دوقلویی‌ها[13] یا حرکت ناهمگن نابجایی‌ها[14] (اثر پورتوین-لوشاتلیه) ناشی از اتم‌های محلول یا برهم‌کنش تهیجایی‌ها با نابجایی‌ها می‌تواند باعث به وجود آمدن این نوع رفتار در مواد شود.[15]

رفتار الاستیک-پلاستیک غیریکنواخت، پلاستیک یکنواخت
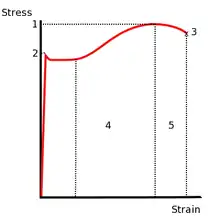
منحنی تنش-کرنش مهندسی یک فولاد سازه‌ای معمولی
۱-استحکام نهایی
۲-استحکام تسلیم
۳-شکست
۴-ناحیه کار سختی
۵-ناحیه گلویی‌شدن

بسیاری از آلیاژهای پایه آهنی و برخی از آلیاژهای غیر آهنی با ساختار مکعبی مرکز پر نقطهٔ تسلیم رفتار خطی از خود نشان می‌دهند ولی پس از تسلیم (تسلیم بالایی) به دلیل تشکیل نوارهای لودر، تنش تا میزان تسلیم پایینی کاهش می‌یابد.[16] سپس بعد از مقداری تغییر شکل در تنش ثابت به دلیل کار سختی دوباره تنش تا استحکام نهایی افزایش می‌یابد.[17] پس از استحکام نهایی به علت گلویی شدن سطح مقطع نمونه کاهش یافته و تنش مهندسی کاهش می‌یابد. این فرایند تا نقطهٔ شکست ادامه پیدا می‌کند.[18]

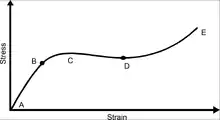
نمودار تنش-کرنش مهندسی در برخی از پلیمرها:
A-B: ناحیه الاستیک
C: تسلیم
C-D: گلویی‌شدن
E: شکست

برخی از پلیمرهای بلورین[19] و شیشه‌ای[20] هنگام تغییر شکل پلاستیک از خود رفتار مشابهی نشان می‌دهند. در این حالت پس از تسلیم بالایی و افت نیرو، کشش سرد آغاز می‌شود که مانند نقطهٔ تسلیم پایینی در فلزات است ولی این ناحیه وسیع‌تر بوده و در آن واحدهای ساختاری پلیمرها در برابر نیرو جهت‌گیری می‌کنند. این فرایند باعث افزایش استحکام پلیمر در برابر نیرو می‌شود.

پانویس
  1. Pilkey, Formulas for stress..., 158.
  2. François , Pineau and Zaoui, Mechanical Behaviour of Materials, 43.
  3. Pelleg, Mechanical Properties of Materials, 7.
  4. Meyers and Chawla, Mechanical Behavior of Materials, 74.
  5. Hertzberg, Deformation and Fracture..., 6.
  6. Pelleg, Mechanical Properties of Materials, 4.
  7. Hertzberg, Deformation and Fracture..., 9.
  8. Hertzberg, Deformation and Fracture..., 9.
  9. Vincent, Structural Biomaterials, 8.
  10. Brinson and Brinson, Polymer Engineering..., 190.
  11. Hertzberg, Deformation and Fracture..., 16.
  12. Hertzberg, Deformation and Fracture..., 28.
  13. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 113.
  14. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 113.
  15. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 164.
  16. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 99.
  17. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 100.
  18. Hertzberg, Vinci and Hertzberg, Deformation and Fracture..., 100.
  19. Hertzberg, Deformation and Fracture..., 30.
  20. Volynskii and Bakeev, Surface Phenomena..., 109.

منابع
  • Brinson, Hal F; Brinson, L. Catherine (2008). Polymer Engineering Science and Viscoelasticity, An Introduction. Springer Science+Business Media. ISBN 978-0-387-73860-4.
  • François, Dominique; Pineau, André; Zaoui, André (1998). Gladwell, G.M.L, ed. Mechanical Behaviour of Materials. Solid Mechanics and Its Applications 57. 1. Dordrecht: Springer Science+Business Media. doi:10.1007/978-94-011-5246-4. ISBN 978-94-010-6207-7.
  • Hertzberg, Richard W (1996). Deformation and Fracture Mechanics of Engineering Materials (4th ed.). USA: John Wiley and Sons, Inc. ISBN 0-471-01214-9.
  • Hertzberg, Richard W; Vinci, Richard P; Hertzberg, Jason L (2013). Deformation and Fracture Mechanics of Engineering Materials (5th ed.). USA: John Wiley and Sons, Inc. ISBN 978-0-470-52780-1.
  • Meyers, Marc André; Chawla, Krishan Kumar (2009). Mechanical Behavior of Materials. UK: Cambridge University Press. ISBN 978-0-521-86675-0.
  • Pelleg, Joshua (2013). Gladwell, G.M.L, ed. Mechanical Properties of Materials. Solid Mechanics And Its Applications 190. Dordrecht: Springer Science+Business Media. doi:10.1007/978-94-007-4342-7. ISBN 978-94-007-4341-0.
  • Pilkey, Walter D (2005). Formulas for stress, strain, and structural matrices (4th ed.). USA: John Wiley and Sons, Inc. ISBN 0-471-03221-2.
  • Vincent, Julian (2012). Structural Biomaterials (3rd ed.). Princeton University Press. ISBN 9780691154008.
  • Volynskii, A. L; Bakeev, N. F (2016). Surface Phenomena in the Structural and Mechanical Behaviour of Solid Polymers. CRC Press. ISBN 978-1-4987-4369-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.