وجه (هندسه)

در هندسه فضایی، یک وجه یا رویه (به انگلیسی: face)، صفحه تخت و بیخمی است که بخشی از مرز یک شیء جامد را سازد.[1] یک جسم سه‌بعدی احاطه‌شده با تعدادی وجه را، چندوجهی نامند.

در حالت تخصصی‌تر هندسه چندوجهی‌ها و چندبرهای با ابعاد بالاتر، وجه، برای نامیدن یک جزء با هر تعداد بُعد از یک چندبر عمومی‌تر (با هر تعداد بُعد) به‌کار می‌رود.[2]

وجه چندضلعی

در هندسهٔ مقدماتی، یک وجه یک چندضلعی دوبعدی است که بر روی مرز یک چندوجهی قرار گرفته است.[2][3]

به عنوان مثال، هر یک از شش مربعی که یک مکعب را احاطه می‌کنند، یک وجه مکعب هستند. همچنین گاهی اوقات، وجه برای نامیدن مشخصهٔ دوبعدی یک ۴-چندبر به‌کار می‌رود. در این کاربرد، فرامکعب ۴-بعدی، ۲۴ وجه مربعی دارد، که هر یک در دو مکعب از ۸ سلول مکعبی فرامکعب به‌کار رفته‌اند.

مثال‌هایی با استفاده از نماد Schläfli
چندوجهی چندوجهی ستاره‌ای کاشی‌کاری اقلیدسی کاشی‌کاری هذلولوی ۴-چندبر
{۴٬۳} {۵/۲٬۵} {۴٬۴} {۴٬۵} {۴٬۳٬۳}

مکعب ۳ وجه مربعی به‌ازای هر رأس دارد.
دوازده‌وجهی ستاره‌ای، ۵ وجه ستاره پنج‌پر به‌ازای هر رأس دارد.
کاشی‌کاری مربعی در صفحهٔ اقلیدسی، ۴ وجه مربعی به‌ازای هر رأس دارد.
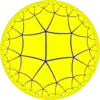کاشی‌کاری مربعی مرتبه ۵، ۵ وجه مربعی به‌ازای هر رأس دارد.
فرامکعب، ۳ وجه مربعی به‌ازای هر لبه دارد.

k-وجه

در هندسه ابعاد بالاتر، وجه‌های یک چندبر، مشخصه‌هایی با ابعاد مختلف هستند.[2][4][5] یک وجه با ابعاد k یک k-وجه نامیده می‌شود. برای مثال، وجه‌های یک چندوجهی معمولی (۳بعدی)، ۲-وجه هستند. در نظریه مجموعه‌ها، مجموعه وجه‌های یک چندبر، شامل خود چندبر و مجموعه تهی هم می‌شود که به مجموعه تهی، برای سازگاری، بعد ۱- داده می‌شود. بنابراین برای هر n-چندبر (چندبر n-بعدی)، k می‌تواند بین ۱- تا n یا خود این اعداد باشد.

برای مثال، با این تعریف، وجه‌های یک مکعب، شامل مجموعه تهی، رأس‌های آن (۰-وجه)، اضلاع آن (۱-وجه)، سطوح مربعی (۲-وجه) و خود مکعب (۳-وجه) هستند.

پانویس
  1. Merriam-Webster's Collegiate Dictionary. Springfield, MA: Merriam-Webster. ۲۰۰۴.
  2. Jiří Matoušek (۲۰۰۲)، «۵٫۳ Faces of a Convex Polytope»، Lectures in Discrete Geometry، Graduate Texts in Mathematics، ۲۱۲، Springer، ص. ۸۶
  3. Cromwell, Peter R. (1999), Polyhedra, Cambridge University Press, p. 13.
  4. Grünbaum, Branko (2003), Convex Polytopes, Graduate Texts in Mathematics, 221 (2nd ed.), Springer, p. 17.
  5. Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, 152, Springer, Definition 2.1, p. 51.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.