پس‌انتشار

پس‌انتشار[1] (انگلیسی: Backpropagation‎) یا انتشار معکوس، روشی در یادگیری عمیق شبکه‌های عصبی مصنوعی، با بیش از یک لایه پنهان است، که برای محاسبه دقیق تر گرادیان وزن مورد استفاده قرار می‌گیرد. این روش اغلب با بهینه‌سازی الگوریتم یادگیری و تثبیت وزن نورون‌ها با محاسبه گرادیان کاهشی تابع هزینه انجام می‌گیرد. این الگوریتم همچنین برای شبکه عصبی پیشخور که نیاز به یادگیری با نظارت دارند، نیز استفاده می‌شود.[2]

ساختار ریاضی الگوریتم

محاسبه گرادیان تابع هزینه برای سلول c

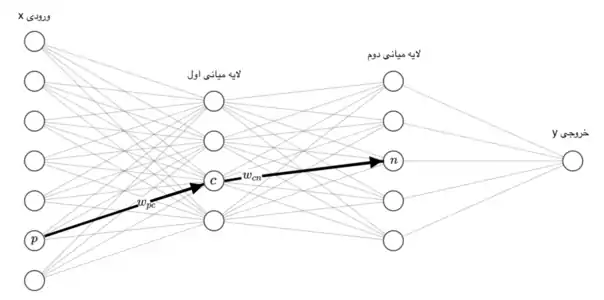
برای سلول عصبی ${\displaystyle c}$ ورودیی که از سلول عصبی ${\displaystyle p}$ به این سلول وارد می‌شود را با ${\displaystyle b_{pc}}$ نشان می‌دهیم. وزن این ورودی ${\displaystyle w_{pc}}$ است و مجموع ضرب ورودی‌ها با وزنهایشان را با ${\displaystyle a_{c}}$ نمایش می‌دهیم، یعنی ${\displaystyle a_{c}=\sum w_{pc}\times b_{pc}}$. حال باید بر روی ${\displaystyle a_{c}}$ یک تابع غیر خطی اعمال کنیم، این تابع را ${\displaystyle \theta _{c}}$ می‌نامیم و خروجی آن را با ${\displaystyle b_{c}}$ نمایش می‌دهیم به این معنی که ${\displaystyle b_{c}=\theta _{c}(a_{c})}$. به همین شکل خروجی‌هایی که از سلول عصبی ${\displaystyle c}$ خارج شده و به سلول ${\displaystyle n}$ وارد می‌شوند را با ${\displaystyle b_{cn}}$ نمایش می‌دهیم و وزن آن را با ${\displaystyle w_{cn}}$ . اگر تمام وزنهای این شبکه عصبی را در مجموعه‌ای به اسم ${\displaystyle W}$ بگنجانیم، هدف در واقع یادگیری این وزنهاست.[3] اگر ورودی ما ${\displaystyle x}$ باشد و خروجی ${\displaystyle y}$ و خروجی شبکه عصبی ما ${\displaystyle h_{W}(x)}$، هدف ما پیدا کردن ${\displaystyle W}$ است به قسمی که برای همه داده‌ها ${\displaystyle y}$ و ${\displaystyle h_{W}(x)}$ به هم خیلی نزدیک شوند. به عبارت دیگر هدف کوچک کردن یک تابع ضرر بر روی تمام داده هاست، اگر داده‌ها را با ${\displaystyle (x_{1},y_{1}),\cdots ,(x_{n},y_{n})}$ و تابع ضرر را با ${\displaystyle l}$ نشان دهیم هدف کمینه کردن تابع پایین بر حسب ${\displaystyle W}$ است:[4]

${\displaystyle Q(W)=\sum _{i=1}^{n}l\left(h_{W}(x_{i}),\,\,y_{i}\right)}$

به عنوان مثال اگر مسئله رگرسیون است برای ${\displaystyle l}$ می‌توانیم خطای مربعات را در نظر بگیریم و اگر مسئله دسته‌بندی است برای ${\displaystyle l}$ می‌شود منفی لگاریتم بازنمایی را استفاده کرد.

برای بدست آوردن کمینه ${\displaystyle Q(W)}$ می‌توان از روش گرادیان کاهشی استفاده کرد، به این معنی که گرادیان تابع را در حساب کرد و کمی در خلاف جهت آن حرکت کرد و این کار را آنقدر ادامه داد تا تابع ضرر خیلی کوچک شود. روش بازگشت به عقب در واقع روشی برای پیدا کردن گرادیان تابع است.

حال فرض کنیم می‌خواهیم گرادیان تابع ${\displaystyle Q(W)}$ را نسبت به وزن ${\displaystyle w_{pc}}$ بدست بیاوریم. برای این کار نیاز به قاعده زنجیری در مشتق‌گیری داریم. قاعده زنجیری به این شکل کار می‌کند: اگر تابعی داشته باشیم به اسم ${\displaystyle f}$ که وابسته به سه ورودی ${\displaystyle u}$، ${\displaystyle v}$ و ${\displaystyle w}$ باشد و هرکدام از این سه ورودی به نوبه خود وابسته به ${\displaystyle t}$ باشند، مشتق ${\displaystyle f}$ به ${\displaystyle t}$ به این شکل محاسبه می‌شود:

${\displaystyle {\frac {\partial f\left(u(t),v(t),w(t)\right)}{\partial t}}={\frac {\partial f}{\partial u}}{\frac {\partial u}{\partial t}}+{\frac {\partial f}{\partial v}}{\frac {\partial v}{\partial t}}+{\frac {\partial f}{\partial w}}{\frac {\partial w}{\partial t}}}$

با استفاده از این قاعده زنجیری روش بازگشت به عقب را به این شکل دنبال می‌کنیم:

${\displaystyle \delta _{c}={\frac {\partial Q}{\partial a_{c}}}}$

${\displaystyle a_{c}=\sum _{p}w_{pc}\times b_{pc}}$

${\displaystyle b_{c}=\theta _{c}(a_{c})}$

${\displaystyle \delta _{c}={\frac {\partial Q}{\partial a_{c}}}={\frac {\partial Q}{\partial b_{c}}}{\frac {\partial b_{c}}{\partial a_{c}}}={\frac {\partial Q}{\partial b_{c}}}\times {\acute {\theta }}_{c}(a_{c})=\left(\sum _{n}{\frac {\partial Q}{\partial a_{n}}}{\frac {\partial a_{n}}{\partial b_{c}}}\right)\times {\acute {\theta }}_{c}(a_{c})=\left(\sum _{n}w_{cn}\delta _{n}\right)\times {\acute {\theta }}_{c}(a_{c})}$

${\displaystyle {\frac {\partial Q}{\partial w_{pc}}}={\frac {\partial Q}{\partial a_{c}}}{\frac {\partial a_{c}}{\partial w_{pc}}}=\delta _{c}b_{p}}$

همان‌طور که در خط پیشین دیدیم برای بدست آوردن گرادیان نسبت به ${\displaystyle w_{pc}}$ به دو مقدار نیاز داریم ورودی به سلول عصبی ${\displaystyle c}$ از سلول عصبی ${\displaystyle p}$ که همان ${\displaystyle b_{p}}$ است و راحت بدست می‌آید و ${\displaystyle \delta _{c}}$ که از روش بازگشتی بدست می‌آید و بستگی به آن ${\displaystyle \delta }$‌هایی لابه بعد دارد که سلول ${\displaystyle c}$به آن‌ها وصل است، به‌طور دقیقتر ${\displaystyle \delta _{c}=\left(\sum _{n}w_{cn}\delta _{n}\right)\times {\acute {\theta }}_{c}(a_{c})}$.

روش بازگشتی برای بدست آوردن ${\displaystyle \delta }$‌ها به این شکل کار می‌کند که ابتدا ${\displaystyle \delta }$ را برای سلول‌های لایه خروجی حساب می‌کنیم، و بعد لایه‌ها را به نوبت پایین می‌روم و برای هر سلول ${\displaystyle \delta }$ آن را با ترکیت ${\displaystyle \delta }$‌های لایه‌های بالایی آن طبق فرمول حساب می‌کنیم. محاسبه کردن ${\displaystyle \delta }$ برای لایه خروجی آسان است و مستقیماً با مشتق گرفتن از ${\displaystyle Q}$ بدست می‌آید.[5]

جستارهای وابسته

• شبکه عصبی مصنوعی
• شبکه عصبی
• آدابوست
• بیش‌برازش
• گرادیان کاهشی تصادفی
• قاعده زنجیری

منابع

1. مقایسه دو الگوریتم پس انتشار خطا و ژنتیک در یادگیری شبکه عصبی برای پیش‌بینی سری زمانی آشوبگونه. زهرا عربسرخی، محمدرضا اصغری اسکویی
2. «Build with AI | DeepAI». DeepAI. بایگانی‌شده از اصلی در 17 اكتبر 2018. دریافت‌شده در 2018-10-24. تاریخ وارد شده در |archivedate= را بررسی کنید (کمک)
3. A., Nielsen, Michael (2015). "Neural Networks and Deep Learning". Archived from the original on 22 اكتبر 2018. Retrieved 23 اكتبر 2018. Check date values in: |access-date=, |archive-date= (help)
4. A., Nielsen, Michael (2015). "Neural Networks and Deep Learning". Archived from the original on 22 اكتبر 2018. Retrieved 23 اكتبر 2018. Check date values in: |access-date=, |archive-date= (help)
5. Russell, Stuart; results, search (2009-12-11). Artificial Intelligence: A Modern Approach (به English) (3 ed.). Boston Columbus Indianapolis New York San Francisco Upper Saddle River Amsterdam, Cape Town Dubai London Madrid Milan Munich Paris Montreal Toronto Delhi Mexico City Sao Paulo Sydney Hong Kong Seoul Singapore Taipei Tokyo: Pearson. p. 578. ISBN 9780136042594.

• مشارکت‌کنندگان ویکی‌پدیا. «Backpropagation». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۹ آوریل ۲۰۱۸.