شبکه عصبی پیشخور

یک شبکه عصبی پیشخور (به انگلیسی: Feedforward Neural Network) یک شبکه عصبی مصنوعی است، که در آن اتصال میان واحدهای تشکیل دهنده آن یک چرخه را تشکیل نمی‌دهند. در واقع این شبکه متفاوت از شبکه‌های عصبی بازگشتی می‌باشد.

در شبکه عصبی پیشخور اطلاعات فقط در یک جهت حرکت می‌کنند.

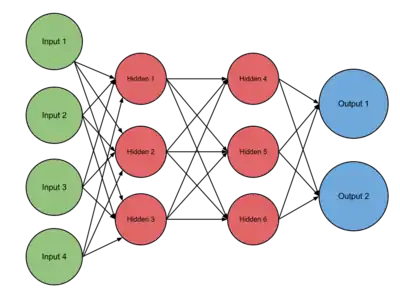
شبکه عصبی پیشخور اولین و ساده‌ترین نوع شبکه عصبی مصنوعی می‌باشد. در این شبکه اطلاعات تنها از یک مسیر حرکت می‌کند که جهت آن رو به جلو می‌باشد. در واقع اطلاعات باشروع از گره (نورون)های ورودی و گذر از لایه‌های پنهان (درصورت وجود) به سمت گره‌های خروجی می‌روند. همان‌طور که گفته شد در این شبکه حلقه یا دوری وجود ندارد.

مقدمه

در سال ۱۹۴۳ وارن مک کلاچ و والتر پیتز اولین نورون مصنوعی را طراحی کردند. خصوصیت اصلی مدل نورون طراحی شده این بود که مجموع سیگنال‌های ورودی وزن دار شده را با یک مقدار آستانه مقایسه می‌کرد و به این ترتیب در مورد خروجی تصمیم‌گیری می‌نمود. این نورون در صورتی که مجموع وزن‌دار شده سیگنال‌ها، کمتر از آستانه بود، خروجی صفر و در غیر اینصورت مقدار ۱ را به عنوان خروجی تولید می‌کرد. آن‌ها قصد داشتند، نشان دهند، یک نورون با چنین خصوصیاتی قادر به محاسبه هر تابع ریاضی یا منطقی می‌باشد. در اواخر دهه ۱۹۵۰ میلادی، فرانک روزنبلات و چندین محقق دیگر، یک کلاس از شبکه‌های عصبی تحت عنوان شبکه‌های عصبی پرسپترون معرفی کردند. نورون‌ها در این شبکه مشابه نورون‌های طراحی شده توسط مک کلاچ و پیتز بودند. روزنبلات ثابت کرد که قاعده یادگیری طراحی شده توسط او در آموزش شبکه‌های پرسپترون همواره به وزن‌های صحیحی همگرا می‌شود. به این ترتیب این شبکه‌ها در صورت وجود پاسخ، حتماً مسئله را حل می‌کردند. روند یادگیری ساده و خودکار بود، همچنین شبکه‌های پرسپترون حتی با شروع از مقادیر تصادفی وزن‌ها و بایاس‌ها قادر به یادگیری و حل مسئله می‌باشند. شایان توجه است که شبکه‌های پرسپترون دارای محدودیت‌هایی نیز می‌باشند. امروزه شبکه‌های پرسپترون دارای اهمیت ویژه‌ای بوده و یک راه‌حل سریع و مطمئن برای حل مسائل طبقه‌بندی شده می‌باشند.

قواعد یادگیری

در مباحث مربوط به شبکه‌های عصبی، قواعد یادگیری، رویه‌ای برای اصلاح وزن‌ها و بایاس‌ها تعریف می‌کنیم. قاعده یادگیری در راستای آموزش شبکه برای انجام کار خاصی مورد استفاده قرار می‌گیرد. قواعد یادگیری به سه بخش عمده تقسیم‌بندی می‌شوند:قاعده یادگیری با نظارت، قاعده یادگیری بی نظارت و قاعده یادگیری تقویتی. در اینجا توضیح مختصری در مورد نحوه عملکرد این قواعد می‌دهیم. در "'قاعده یادگیری با نظارت"' از مجموعه‌ای از نمونه‌های آموزشی استفاده می‌کنیم که شبکه را آموزش می‌دهند. زوج‌های مرتب زیر را در نظر بگیرید:

${\displaystyle \left({x_{1},y_{1}}\right),\left({x_{2},y_{2}}\right),\left({x_{3},y_{3}}\right),...,\left({x_{n},y_{n}}\right)}$

در هر زوج مرتب، ${\displaystyle x_{i}}$، ورودی شبکه و ${\displaystyle y_{i}}$ به عنوان خروجی یا هدف مورد نظر شناخته می‌شود. زمانی که ورودی به شبکه اعمال می‌شود، خروجی با هدف مقایسه می‌شود. سپس بر طبق قواعد یادگیری برای تنظیم وزن‌ها و بایاس‌ها تغییرات لازم اعمال می‌گردد تا خروجی شبکه به هدف مورد نظر نزدیک تر شود. قاعده یادگیری شبکه‌های پرسپترون از همین نوع می‌باشد. در "' قاعده یادگیری بی نظارت"' وزن‌ها و بایاس‌ها تنها در مقابل ورودی شبکه اصلاح می‌شوند و در واقع هیچ هدفی وجود ندارد. این الگوریتم اکثراً برای عملیات دسته‌بندی استفاده می‌شود. آن‌ها ورودی‌ها را با داشتن تعداد محدودی از کلاس‌ها دسته‌بندی می‌کنند. "'قاعده یادگیری تقویتی"' بر رفتارهایی تمرکز دارد که ماشین باید برای بیشینه کردن پاداشش انجام دهد. این مسئله، با توجه به گستردگی‌اش، در زمینه‌های گوناگونی بررسی می‌شود. مانند: نظریه بازی‌ها، نظریه کنترل، هوش ازدحامی، آمار و …. این نوع یادگیری در شبکه‌های پرسپترون و یادگیری بدون نظارت در شبکه پرسپترون کاربردی ندارند و توضیح بیشتر در مورد آنان از حوصله بحث خارج است.

یادگیری از طریق بازگشت به عقب

یادگیری ماشینی با نظارت (supervised learning) به دنبال تابعی از میان یک سری توابع هست که تابع هزینه (loss function) داده‌ها را بهینه سازد. به عنوان مثال در مسئله رگرسیون تابع هزینه می‌تواند اختلاف بین پیش‌بینی و مقدار واقعی خروجی به توان دو باشد، یا در مسئله طبقه‌بندی ضرر منفی لگاریتم احتمال خروجی باشد. مشکلی که در یادگیری شبکه‌های عصبی وجود دارد این است که این مسئله بهینه‌سازی دیگر محدب (convex) نیست.[1] ازین رو با مشکل کمینه‌های محلی روبرو هستیم. یکی از روش‌های متداول حل مسئله بهینه‌سازی در شبکه‌های عصبی بازگشت به عقب یا همان back propagation است.[1] روش بازگشت به عقب گرادیانِ تابع هزینه را برای تمام وزن‌های شبکه عصبی محاسبه می‌کند و بعد از روش‌های گرادیان کاهشی (gradient descent) برای پیدا کردن مجموعه وزن‌های بهینه استفاده می‌کند.[2] روش‌های گرادیان کاهشی سعی می‌کنند به صورت متناوب در خلاف جهت گرادیان حرکت کنند و با این کار تابع هزینه را به حداقل برسانند.[2] پیدا کردن گرادیانِ لایه آخر ساده است و با استفاده از مشتق جزئی بدست می‌آید. گرادیانِ لایه‌های میانی اما به صورت مستقیم بدست نمی‌آید و باید از روش‌هایی مانند قاعده زنجیری در مشتق‌گیری استفاده کرد.[2] روش بازگشت به عقب از قاعده زنجیری برای محاسبه گرادیان‌ها استفاده می‌کند و همان‌طور که در پایین خواهیم دید، این روش به صورت متناوب گرادیان‌ها را از بالاترین لایه شروع کرده آن‌ها را در لایه‌های پایینتر «پخش» می‌کند.

تصویری از یک شبکه عصبی با دو لایه پنهان، گرادیان c وابسته به گرادیان لایه‌های بالاتر است که به آنها متصل است.

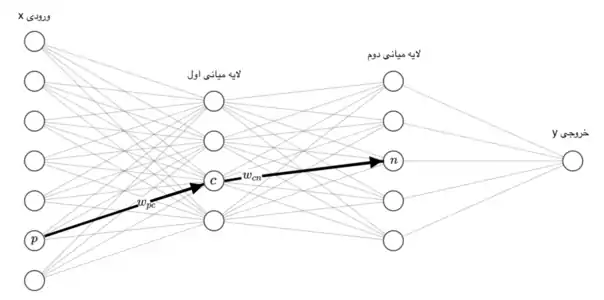
برای سلول عصبی ${\displaystyle c}$ ورودیی که از سلول عصبی ${\displaystyle p}$ به این سلول وارد می‌شود را با ${\displaystyle b_{pc}}$ نشان می‌دهیم. وزن این ورودی ${\displaystyle w_{pc}}$ است و مجموع ضرب ورودی‌ها با وزنهایشان را با ${\displaystyle a_{c}}$ نمایش می‌دهیم، به این معنی که ${\displaystyle a_{c}=\sum _{p}w_{pc}\times b_{pc}}$. حال باید بر روی ${\displaystyle a_{c}}$ تابعی غیر خطی اعمال کنیم این تابع را ${\displaystyle \theta _{c}}$ می‌نامیم و خروجی آن را با ${\displaystyle b_{c}}$ نمایش می‌دهیم یعنی ${\displaystyle b_{c}=\theta _{c}(a_{c})}$. به همین شکل خروجیی که از سلول عصبی ${\displaystyle c}$ خارج شده و به سلول ${\displaystyle n}$ وارد می‌شود را با ${\displaystyle b_{cn}}$ نمایش می‌دهیم و وزن آن را ${\displaystyle w_{cn}}$ می‌نامیم. حال تمام وزن‌های این شبکه عصبی را در مجموعه‌ای به اسم ${\displaystyle W}$ می‌گنجانیم، هدف یادگیری این وزنهاست.[3] اگر ورودی ما ${\displaystyle x}$ باشد و خروجی ${\displaystyle y}$ و خروجی شبکه عصبی ما ${\displaystyle h_{W}(x)}$، هدف پیدا کردن انتخاب ${\displaystyle W}$ است به قسمی که برای تمام داده‌ها ${\displaystyle y}$ و ${\displaystyle h_{W}(x)}$ به هم خیلی نزدیک شوند. به عبارت دیگر هدف کوچک کردن یک تابع هزینه بر روی تمام داده هاست، اگر داده‌ها را با ${\displaystyle (x_{1},y_{1}),\cdots ,(x_{n},y_{n})}$ و تابع هزینه را با ${\displaystyle l}$ نشان دهیم هدف کمینه کردن تابع پایین است:[4]

${\displaystyle Q(W)=\sum _{i=1}^{n}l\left(h_{W}(x_{i}),\,\,y_{i}\right)}$

به عنوان مثال اگر مسئله رگرسیون است برای ${\displaystyle l}$ می‌توانیم خطای مربعات را در نظر بگیریم و اگر مسئله دسته‌بندی است برای ${\displaystyle l}$می‌شود منفی لگاریتم بازنمایی را استفاده کرد.

برای بدست آوردن کمینه ${\displaystyle Q(W)}$ باید از روش گرادیان کاهشی استفاده کرد، به این معنی که گرادیان تابع را حساب کرده، کمی در خلاف جهت آن حرکت کرده و این کار را آنقدر ادامه داد تا تابع هزینه خیلی کوچک شود. روش بازگشت به عقب در واقع روشی برای پیدا کردن گرادیان تابع ${\displaystyle Q(W)}$ است.

حال فرض کنیم می‌خواهیم گرادیان تابع ${\displaystyle Q(W)}$ را نسبت به وزن ${\displaystyle w_{pc}}$ بدست بیاوریم. برای این کار نیاز به قاعده زنجیری در مشتق‌گیری داریم. قاعده زنجیری به این شکل کار می‌کند: اگر تابعی داشته باشیم به اسم ${\displaystyle f}$ که وابسته به سه ورودی ${\displaystyle u}$، ${\displaystyle v}$ و ${\displaystyle w}$ باشد و هرکدام از این سه ورودی به نوبه خود وابسته به ${\displaystyle t}$ باشند، مشتق ${\displaystyle f}$ به ${\displaystyle t}$ به این شکل محاسبه می‌شود:

${\displaystyle {\frac {\partial f\left(u(t),v(t),w(t)\right)}{\partial t}}={\frac {\partial f}{\partial u}}{\frac {\partial u}{\partial t}}+{\frac {\partial f}{\partial v}}{\frac {\partial v}{\partial t}}+{\frac {\partial f}{\partial w}}{\frac {\partial w}{\partial t}}}$

با استفاده از این قاعده زنجیری روش بازگشت به عقب را به این شکل دنبال می‌کنیم:

${\displaystyle \delta _{c}={\frac {\partial Q}{\partial a_{c}}}}$

${\displaystyle a_{c}=\sum _{p}w_{pc}\times b_{pc}}$

${\displaystyle b_{c}=\theta _{c}(a_{c})}$

${\displaystyle \delta _{c}={\frac {\partial Q}{\partial a_{c}}}={\frac {\partial Q}{\partial b_{c}}}{\frac {\partial b_{c}}{\partial a_{c}}}={\frac {\partial Q}{\partial b_{c}}}\times {\acute {\theta }}_{c}(a_{c})=\left(\sum _{n}{\frac {\partial Q}{\partial a_{n}}}{\frac {\partial a_{n}}{\partial b_{c}}}\right)\times {\acute {\theta }}_{c}(a_{c})=\left(\sum _{n}w_{cn}\delta _{n}\right)\times {\acute {\theta }}_{c}(a_{c})}$

${\displaystyle {\frac {\partial Q}{\partial w_{pc}}}={\frac {\partial Q}{\partial a_{c}}}{\frac {\partial a_{c}}{\partial w_{pc}}}=\delta _{c}b_{p}}$

همان‌طور که در خط پیشین دیدیم برای بدست آوردن گرادیان نسبت به ${\displaystyle w_{pc}}$ به دو مقدار نیاز داریم ورودی به سلول عصبی ${\displaystyle c}$ از سلول عصبی ${\displaystyle p}$ که همان ${\displaystyle b_{p}}$ است و راحت بدست می‌آید و ${\displaystyle \delta _{c}}$ که از روش بازگشتی بدست می‌آید و بستگی به ${\displaystyle \delta }$‌هایی لایه بعد دارد که سلول ${\displaystyle c}$به آن‌ها وصل است، به‌طور دقیقتر ${\displaystyle \delta _{c}=\left(\sum _{n}w_{cn}\delta _{n}\right)\times {\acute {\theta }}_{c}(a_{c})}$.

روش بازگشتی برای بدست آوردن ${\displaystyle \delta }$‌ها به این شکل کار می‌کند که ابتدا ${\displaystyle \delta }$ را برای سلول‌های لایه خروجی حساب می‌کنیم، و بعد لایه‌ها را به نوبت پایین آئیم و برای هر سلول ${\displaystyle \delta }$ آن را با ترکیت ${\displaystyle \delta }$‌های لایه‌های بالایی آن طبق فرمول حساب می‌کنیم. محاسبه کردن ${\displaystyle \delta }$ برای لایه خروجی آسان است و مستقیماً با مشتق گرفتن از ${\displaystyle Q}$ بدست می‌آید.[5]

پرسپترون تک لایه

یک نورون پرسپترون که از تابع انتقال hard-limit استفاده می‌کند.

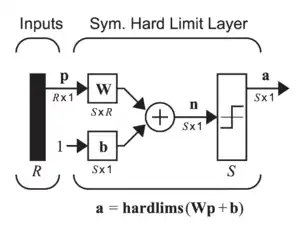
پرسپترون تک لایه ساده‌ترین نوع شبکه عصبی است، که از یک لایه از نورون‌های خروجی تشکیل شده‌است. ورودی‌های این شبکه به وسیله یک آرایه از وزن‌ها به صورت مستقیم به خروجی‌ها نسبت داده می‌شوند. در نتیجه این شبکه لایه پنهانی ندارد. این شبکه را می‌توان ساده‌ترین شبکه عصبی پیشخور دانست. در هر نورون مجموع ضرب هر وزن در ورودی با اندیس برابر خود محاسبه می‌شود. اگر مقدار مجموع محاسبه شده در بالا برای هر نورون بالاتر از یک مقدار آستانه باشد (به‌طور معمول ۰)، نورون فعال شده و مقدار فعال (به‌طور معمول ۱) را می‌پذیرد، در غیر این صورت مقدار غیرفعال (به‌طور معمول -۱) را می‌پذیرد. به نورون‌های با تابع فعال سازی از نوع بالا را نورون‌های مصنوعی یا واحدهای آستانه خطی می‌گوییم. اصطلاح پرسپترون اغلب اشاره به شبکه‌های متشکل از تنها یکی از این واحدها می‌کند.[6]

یک پرسپترون را می‌توان با استفاده از هر مقداری برای حالات فعال و غیرفعال، تا زمانی که مقدار آستانه بین دو مقدار قرار دارد، ساخت. اکثر پرسپترون‌ها خروجی‌هایی از ۱ یا -۱ با مقدار آستانه ۰ دارند. شبکه‌های دارای ساختار بالا را با سرعت بیشتری نسبت به شبکه‌های متشکل از نورون‌های دارای مقادیر مختلف فعال و غیرفعال، می‌توان آموزش داد.[7]

پرسپترون‌ها را می‌توان با یک الگوریتم یادگیری ساده که معمولاً به نام قانون دلتا آن را می‌شناسند، آموزش داد. این الگوریتم خطاهای میان خروجی محاسبه شده و خروجی نمونه را محاسبه کرده و از آن برای بروزرسانی مقادیر وزن‌ها استفاده می‌کند. این الگوریتم نتیجه اجرای یک نمونه از گرادیان کاهشی می‌باشد.

پرسپترون‌های تک‌واحد تنها قادر به یادگیری الگوهای خطی جدا از هم می‌باشد. در سال ۱۹۶۹ در یک مقاله-که بعداً تبدیل به کتاب شد- معروف تحت عنوان «پرسپترون‌ها»،[8] ماروین مینسکی و سیمور پاپرت، نشان دادند که برای یک شبکه پرسپترون تک‌لایه یادگیری تابع بولی XOR غیرممکن است. با این وجود، می‌دانیم است که پرسپترون‌های چند لایه قادر به تولید هر گونه تابع بولی می‌باشند.

اگر چه یک واحد آستانه کاملاً محدود به قدرت محاسباتی خود می‌باشد، اثبات شده‌است که شبکه‌هایی از واحدهای آستانه موازی می‌توانند هر تابع پیوسته از بازه فشرده اعداد حقیقی به بازه [-۱٬۱]. این نتیجه توسط پیتر آور، هارولد برگستینر و ولفگانگ ماس در مقاله‌ای در مورد قوانین و الگوریتم‌های یادگیری با عنوان بدست آمده‌است.[9]

شبکه عصبی چند لایه می‌تواند یک خروجی پیوسته را به جای یک تابع پله‌ای محاسبه کند. یک انتخاب رایج که تابع لجستیک (منطقی) نامیده می‌شود برابر است با:

${\displaystyle f(x)={\frac {1}{1+e^{-x}}}}$

تابع لجیستیک (منطقی) با نام تابع سیگموئید نیز شناخته می‌شود. با این انتخاب، شبکه تک‌لایه با مدل رگرسیون لجستیک یکسان می‌شود. این مدل به صورت گسترده در مدل آماری کاربرد دارد. ضابطه این تابع، دارای مشتق پیوسته و همچنین ضابطه مشتق آن بر حسب خود تابع بدست می‌آید. این ویژگی باعث شده‌است که از این تابع در متد پس‌انتشار استفاده شود. رابطه مشتق این تابع با خود تابع برابر است با:

${\displaystyle f'(x)=f(x)(1-f(x))}$

(این رابطه به راحتی با استفاده از قاعده زنجیری قابل اثبات است)

جستارهای وابسته

• تابع سیگموئید (Sigmoid Function)
• شبکه عصبی (Biological Neural Network)
• شبکه عصبی مصنوعی (Artificial Neural Network)
• یادگیری عمیق (Deep Learning)
• یادگیری تقویتی (Reinforcement learning)
• یادگیری بانظارت (Supervised learning)
• یادگیری بی‌نظارت (Unsupervised learning)

منابع

1. Ian Goodfellow and Yoshua Bengio and Aaron Courville (۲۰۱۶). Deep learning. MIT Press. صص. ۲۰۰.
2. Heaton, Jeff (2017-10-29). "Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep learning". Genetic Programming and Evolvable Machines. 19 (1–2): 305–307. doi:10.1007/s10710-017-9314-z. ISSN 1389-2576.
3. «Build with AI | DeepAI». DeepAI. بایگانی‌شده از اصلی در 17 اكتبر 2018. دریافت‌شده در 2018-10-24. تاریخ وارد شده در |archivedate= را بررسی کنید (کمک)
4. A., Nielsen, Michael (2015). "Neural Networks and Deep Learning". Archived from the original on 22 اكتبر 2018. Retrieved 13 دسامبر 2019. Check date values in: |archive-date= (help)
5. Russell, Stuart; results, search (2009-12-11). Artificial Intelligence: A Modern Approach (به English) (3 ed.). Boston Columbus Indianapolis New York San Francisco Upper Saddle River Amsterdam, Cape Town Dubai London Madrid Milan Munich Paris Montreal Toronto Delhi Mexico City Sao Paulo Sydney Hong Kong Seoul Singapore Taipei Tokyo: Pearson. p. 578. ISBN 9780136042594.
6. Kasabov, N. K (1998). Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering. MIT Press. ISBN 0-262-11212-4.
7. T.Hagan, Martin; B.Demuth, Howard; Beale, Mark (1996). Neural Networks Design. PWS Publishing Co. Boston. ISBN 0-534-94332-2.
8. L.Minsky, Marvin; Papert, Seymour (1988). Perceptrons: An Introduction to Computational Geometry. The MIT Press. ISBN 0-262-63111-3.
9. Auer, Peter; Harald Burgsteiner; Wolfgang Maass (2008). "A learning rule for very simple universal approximators consisting of a single layer of perceptrons" (PDF). Neural Networks. doi:10.1016/j.neunet.2007.12.036. Archived from the original (PDF) on 6 July 2011. Retrieved 27 April 2017.

پیوند به بیرون

• الگوریتمی ترکیبی برای آموزش شبکه‌های عصبی مصنوعی
• انجمن آمریکایی هوش مصنوعی
• هوش مصنوعی - MIT
• کتابخانه هوش مصنوعی