اصل کمترین کنش

اصلِ کمترین کُنش اصلی در فیزیک است که بسیاری از قوانینِ فیزیک از آن به دست می‌آیند. به عبارتِ علمی‌تر؛ این اصل – یا دقیق‌تر اصلِ کُنشِ ثابت – یک اصل وردشی است که هنگامی که به کنش یک سیستم مکانیکی اعمال شود، معادلات حرکت آن سیستم به دست می‌آید.

از این اصل برای به دست آوردن معادلاتِ حرکتِ مکانیکِ نیوتنی و مکانیک لاگرانژی و مکانیک هامیلتونی و حتی نسبیت عام[1] استفاده کرد.

از لحاظ تاریخی علت استفاده از واژهٔ «کمترین» این بود که راه حلی در حساب وردشی برای پیدا کردنِ کوتاهترین مسیر از میانِ مسیرهای موجود یافته شود.[2] این اصل به ایجاد مکانیک کوانتومی کمک کرد.[3]

بیان عمومی

با تکامل سیستم q مسیرهای ممکنی را در فضای پیکربندی در پیش می‌یابد (تنها برخی از آنها نشان داده شده است). مسیر انتخاب شده توسط سیستم (قرمز) کنش ثابت (δS = 0) تحت تغییرات کوچک در پیکربندی سیستم (δq) را داراست.[4]

با کنش یک سیستم فیزیکی شروع می‌کنیم، که با (خوشنویسی s) نمایانده می‌شود.

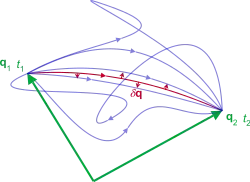
کنش به عنوان انتگرال از لاگرانژین L بین دو زمان t₁ و t₂ تعریف می‌شود. از لحاظ فنی کنش یک تابعی از N مختصه تعمیم‌یافته
q = (q1, q2 ... qN) که پیکربندی سیستم را تعریف می‌کنند، است.

{\mathcal {S}}[\mathbf {q} (t)]=\int _{t_{1}}^{t_{2}}L(\mathbf {q} (t),\mathbf {\dot {q}} (t),t)dt

که در آن نقطه نشان دهنده مشتق زمانی و t زمان است.

به صورت ریاضی این اصل به این شکل است[5][6][7]

\delta {\mathcal {S}}=0

که در آن δ (حروف کوچک یونانی دلتا) به معنی تغییر کوچک است. به صورت کلماتی این چنین خوانده می‌شود:[4]

مسیر انتخاب شده توسط سیستم بین زمان t₁ و t₂به گونه‌ای است که کنش تا مرتبه اول مشتق، ثابت (بدون تغییر) است.

در عمل این انتگرال و تعریف در کنار هم قرار گرفته و چنین نتیجه‌ای می‌دهد:[8]

\delta \int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)dt=0

یادداشت ها و منابع

کنش اینشتین-هیلبرت را ببینید
Chapter 19 of Volume II, Feynman R, Leighton R, and Sands M. The Feynman Lectures on Physics . 3 volumes 1964, 1966.
"The Character of Physical Law" Richard Feynman
R. Penrose (2007).
Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3
Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0
Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] کنش اینشتین-هیلبرت را ببینید

[2] Chapter 19 of Volume II, Feynman R, Leighton R, and Sands M. The Feynman Lectures on Physics . 3 volumes 1964, 1966.

[ReferenceA-3] "The Character of Physical Law" Richard Feynman

[penrose-4] R. Penrose (2007).

[5] Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3

[6] McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3

[Analytical_Mechanics_2008-7] Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978-0-521-57572-0

[8] Classical Mechanics, T.W.B. Kibble, European Physics Series, McGraw-Hill (UK), 1973, ISBN 0-07-084018-0