توزیع لوی
در نظریه آمار و احتمالات، توزیع لِوی یک توزیع احتمالی پیوستهاست که برای یک متغیر تصادفی غیر منفی تعریف میشود. در طیفسنجی، این توزیع که در آن فرکانس متغیر وابسته است، با نامِ پروفیل ون در والس شناخته میشود.[1] همچنین این توزیع یک مورد خاص از توزیع گامای وارونه است. توزیع لِوی یک توزیع پایدار است.[2]
|
تابع چگالی احتمال 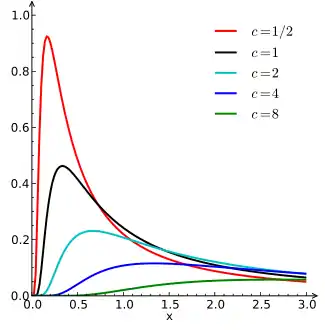 | |||
|
تابع توزیع تجمعی 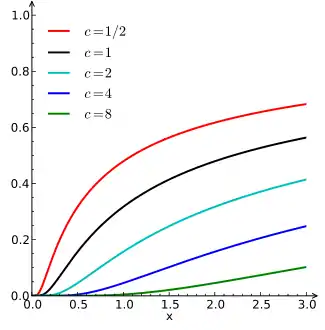 | |||
| فراسنجهها | location; scale | ||
|---|---|---|---|
| تکیهگاه | |||
| تابع چگالی احتمال | |||
| تابع توزیع تجمعی | |||
| میانگین | |||
| میانه | , for | ||
| مُد | , for | ||
| واریانس | |||
| چولگی | undefined | ||
| کشیدگی | undefined | ||
| آنتروپی |
where is Euler's constant | ||
| تابع مولد گشتاور | undefined | ||
| تابع مشخصه | |||
تعریف
تابع چگالی احتمال توزیع لوی در دامنه برابر است با:
در اینجا پارامتر مکان و پارامتر مقیاس است. تابع توزیع تجمعی توزیع برابر است با:
در اینجا تابع خطای مکمل است. پارامتر تغییر مکانِ کل منحنی را به سمت راست به اندازه منتقل میکند. مانند تمام توزیعهای پایدار، توزیع لِوی یک شکل استاندارد دارد که خاصیت پایین را دارا میباشد:
در اینجا با مقدار پایین برابر است:
تابع مشخصهی توزیع لِوی برابر است با:
این تابع مشخصه همچنین میتواند به همان شکلی که برای توزیع پایدار با و نوشته میشود، نوشته شود.
گشتاور ام توزیع لِوی با فرض اینکه باشد برابر است با:
تمامی این گشتاورها واگرا هستند. این به این معنی است که این گشتاورها در واقع وجود ندارند. همچنین تابع مولد گشتاورها به این شکل تعریف میشود:
همانطور که معادله خط پیشین نشان میدهد برای تمام مقدار انتگرال واگراست و در اطراف صفر تعریف نشدهاست. از این رو تابع مولد گشتاور نیز تعریف نشدهاست. مضاف بر این مانند تمام توزیعهای پایدار به غیر از توزیع طبیعی، این توزیع دمسنگین و دمکلفت است، یعنی برای تابع به معادله پایین میل میکند:
این خصیصه در شکل پایین به خوبی نشان داده شدهاست. در اینجا و بردارها در مقیاس لگاریتمی رسم شدهاند.
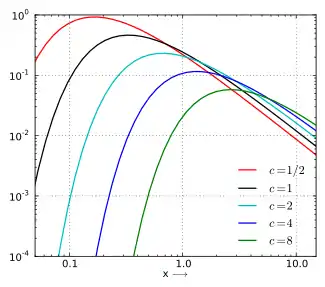
توزیع استاندارد لِوی شرایط یک توزیع پایدار را برآورده میکند:[3]
در اینجا متغیرهای تصادفی مستقلی هستند که همگی از توزیع استاندارد لِوی متابعت میکنند، در اینجا .
توزیعهای مرتبط
- اگر آنگاه
- اگر آنگاه
- اگر آنگاه
- اگر آنگاه
- اگر آنگاه
- اگر آنگاه
- اگر آنگاه
تولید نمونههای تصادفی
نمونههای تصادفی از توزیع لِوی میتواند از طریق روش تبدیل معکوس ایجاد شود. با فرض اینکه متغیر تصادفی از یک توزیع یکنواخت در فاصله واحد گرفته شده باشد، آنگاه توزیع متغیر که در پایین تعریف شدهاست لِوی خواهد بود:[4]
در اینجا تابع توزیع تجمعی طبیعی است.
منابع
- Maslov, V. P. (2015-04-01). "Van der Waals equation from the viewpoint of probability distribution and the triple point as the critical point of the liquid-to-solid transition". Russian Journal of Mathematical Physics. 22 (2): 188–200. doi:10.1134/S1061920815020065. ISSN 1555-6638.
- Sato, Ken-iti; Ken-Iti, Sato (1999-11-11). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press. ISBN 9780521553025.
- Barndorff-Nielsen, Ole E.; Mikosch, Thomas; Resnick, Sidney I. (2001-03-30). Lévy Processes: Theory and Applications. Springer Science & Business Media. ISBN 9780817641672.
- How to derive the function for a random sample from a Lévy Distribution: http://www.math.uah.edu/stat/special/Levy.html
یادداشتها
- "Information on stable distributions". Archived from the original on 30 اكتبر 2006. Retrieved July 13, 2005. Check date values in:
|archive-date=(help) - John P. Nolan's introduction to stable distributions, some papers on stable laws, and a free program to compute stable densities, cumulative distribution functions, quantiles, estimate parameters, etc. See especially بایگانیشده در ۱۷ ژوئیه ۲۰۱۱ توسط Wayback Machine An introduction to stable distributions, Chapter 1