جامد اینشتین

جامد اینشتین مدلی ساده برای جامدات است که بر مبنای ۳ فرض اصلی بنا شده‌است:

۱- اتمهای مجاور هم در شبکه جسم جامد برهمکنشی با هم ندارند.

۲-هر اتم در شبکه مثل یک نوسانگر هماهنگ سه بعدی رفتار می‌کند. ترازهای انرژی هر نوسانگر، بر اساس الگوی کوانتش پلانک، گسسته‌اند و فاصلهٔ جدایی ترازها ${\displaystyle h\nu }$ است.

۳- همهٔ نوسانگرها با بسامد یکسانی در ارتعاشند.

علامت	مفهوم
Z	تابع پارش
${\displaystyle E_{n}}$	انرژی در تراز nام
k	ثابت بولتزمان
${\displaystyle \nu }$	بسامد ارتعاش
${\displaystyle h}$	ثابت پلانک
T	دمای مطلق
${\displaystyle \theta _{E}}$	دمای اینشتین
F	انرژی آزاد هلمولتز
S	انتروپی
V	حجم
M	تعداد اتم‌های جامد
E	انرژی داخلی
${\displaystyle C_{V}}$	ظرفیت حرارتی در حجم ثابت
R	ثابت جهانی گازها

مکانیک آماری
ترمودینامیک نظریه جنبشی
آمار ذرات تئوری چرخش-آمار ذرات یکسان ماکسول بولتزمن بوز-اینشتین فرمی-دیراک Parastatistics Anyonic Statistics Braid Statistics
هنگردهای ترمودینامیک NVE ریزبندادی NVAT بندادی µVAT بزرگ‌بندادی NPH Isoenthalpic–isobaric NPT Isothermal–isobaric µVT Open statistical
مدل‌ها دبای جامد اینشتین ایزینگ پاتس
پتانسیل ترمودینامیکی انرژی درونی آنتالپی انرژی آزاد هلمولتز انرژی آزاد گیبس پتانسیل بزرگ
دانشمندان جیمز کلرک ماکسول لودویگ بولتسمان جوسایا ویلارد گیبس آلبرت اینشتین پائول ارنفست جان فون نویمان ریچارد سی تولمان پیتر دبای انریکو فرمی ساتیندرا بوز

این مدل در سال ۱۹۰۷ توسط آلبرت اینشتین معرفی شد.[1] بدیهی است که فرض اول درست نیست و در واقع بیشتر خواص یک جامد حاصل وجود برهمکنش بین اتم‌های آن است. با این حال، این فرض باعث سادگی مدل می‌شود و برای هدفی که اینشتین از ارائهٔ این مدل داشت، فرض مناسبی است. هدف اصلی اینشتین از ارائهٔ این مدل آن بود که نشان دهد مفهوم کوانتش پلانک می‌تواند بعضی از ناسازگاری‌های فیزیک کلاسیک را حل کند.

در ترمودینامیک کلاسیک ظرفیت گرمایی جامدات بر اساس قانون تجربی دولون-پتی محاسبه می‌شد و سازگاری قابل قبولی با نتایج آزمایشگاهی داشت. قانون دولون-پتی ظرفیت گرمایی بلورها را ${\displaystyle 3Nk}$ پیش‌بینی می‌کند که مستقل از دماست. این نتیجه با دربایست‌های فیزیک کلاسیک کاملاً سازگار است. مشکل زمانی بروز می‌کند که دما را به صفر مطلق نزدیک کنیم. بنا به نتایج تجربی، و بر خلاف قانون دولون-پتی (و به تبعِ آن فیزیک کلاسیک)، وقتی دما به صفر مطلق نزدیک شود ظرفیت گرمایی به سرعت افت کرده و به صفر میل می‌کند.

با این که اینشتین می‌دانست بسامد نوسانات اتم‌های مختلف باید متفاوت باشد، فرض سوم را مبنی بر یکسان بودن بسامد همهٔ نوسان گرها وارد مدل خود کرد. این فرض باعث سادگی بیش از حد مدل می‌شود. نتیجهٔ لحاظ کردن فرض سوم در مدل این بود که: بنا به پیش‌بینی مدل، با نزدیک شدن دما به صفر مطلق، ظرفیت گرمایی به صورت نمایی با دما افت می‌کند. اگر فرض یکسان بودن بسامد نوسان گرها را کنار بگذاریم جواب واقعی تری که امروزه به مدل دبای مشهور است، و بر اساس آن ظرفیت گرمایی به صورت تابعی از ${\displaystyle T^{3}}$ به صفر میل می‌کند، حاصل می‌شد.

خواص

تابع پارش این مدل، یک تصاعد هندسی همگرا به صورت زیر است:

${\displaystyle Z=\sum _{n=0}^{\infty }e^{-E_{n}/kT}={e^{-h\nu /2kT} \over 1-e^{-h\nu /kT}}}$

همانگونه که دیده می‌شود، تابع پارش تنها به ${\displaystyle h\nu /kT}$ وابسته است.

دمای اینشتین (${\displaystyle \theta _{E}}$) به صورت ${\displaystyle h\nu =k\theta _{E}}$ تعریف می‌شود. در اینصورت خواهیم داشت:

${\displaystyle Z={e^{-\theta _{E}/2T} \over 1-e^{-\theta _{E}/T}}}$

انتروپی سیستم را می‌توان به صورت زیر بدست آورد:

${\displaystyle S=-({\frac {\delta F}{\delta T}})_{V}=-({\frac {\delta (-3MkTlnZ)}{\delta T}})_{V}}$

${\displaystyle S=3MkT{\frac {\theta _{E}}{T^{2}}}{e^{-\theta _{E}/2T} \over 1-e^{-\theta _{E}/T}}-3Mkln(1-e^{-\theta _{E}/T})}$

با نزدیک شدن T به صفر، انتروپی سیستم نیز به صفر میل می‌کند که بیانی از قانون سوم ترمودینامیک است.

ظرفیت گرمایی این مجموعه را می‌توان به صورت زیر از انرژی داخلی بدست آورد:

${\displaystyle C_{V}=\left({\frac {\partial E}{\partial T}}\right)_{V}=\left({\frac {\partial (3MkT^{2}{\frac {\partial lnZ}{\partial T}})}{\partial T}}\right)_{V}=3R\left({\frac {\theta _{E}}{T}}\right)^{2}{\frac {e^{\theta _{E}/T}}{(e^{\theta _{E}/T}-1)^{2}}}}$

در دماهای بالا (${\displaystyle T\gg \theta _{E}}$)، ${\displaystyle C_{V}}$ به سمت مقدار ثابت 3R میل می‌کند.[2]

ظرفیت گرمایی جامد انیشتین به دما وابسته بوده و در دماهای بالاتر به مقدار 3Nk میل می‌کند.

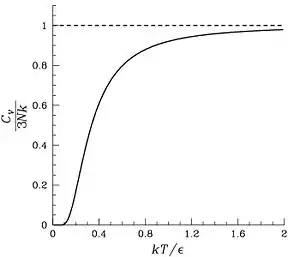
با اینکه در دماهای بالا ظرفیت حرارتی اکثر جامدات به خوبی از این مدل تبعیت می‌کنند اما در دماهای پایین به دلیل برهم‌کنش اتم‌ها با یکدیگر فرضیات اولیهٔ مدل اینشتین صادق نبوده و نتایج آن با خطا همراه هستند. دبای با در نظر گرفتن این برهم‌کنش‌ها، مدل جدیدی برای جامدات ارائه کرد که به جامد دبای معروف است.

پانویس

1. Einestein, 1907
2. Dugdale, 1996

منابع

• Dugdale, J.S. (1996), Entropy And Its Physical Meaning, CRC Press, 2nd ed. , ISBN 0-7484-0569-0
• Einstein, Albert (1907), Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme, Annalen der Physik, Vol. 22, pp. 180-190.