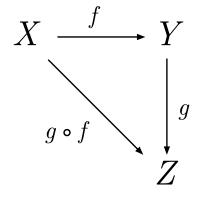رسته (ریاضیات)

یک رسته در ریاضیات، ساختاری جبری است که در آن سازه‌های ریاضی و روابط میان آنها به صورت مجرد بررسی می‌شود. در یک رده، سازه‌ها یا اشیاء و پیکانهای میان آنها مستقل از اینکه اشیاء چه هستند مورد بررسی قرار می‌گیرد.

تعریف

یک رده ${\displaystyle C}$ عبارت است از:

• یک کلاس ${\displaystyle Ob(C)}$ از اشیاء یا سازه‌ها،
• یک کلاس ${\displaystyle hom(C)}$ یا ${\displaystyle mor(C)}$ از پیکانها یا ریختارها (یا مورفیسم‌ها). یک عضو ${\displaystyle f\in hom(C)}$ عبارت است از یک پیکان ${\displaystyle f:a\to b}$ برای دو سازه ${\displaystyle a,b\in Ob(C)}$. نویسه ${\displaystyle hom(a,b)}$ نمایانگر کلاس پیکانهای میان دو شی${\displaystyle a}$ و ${\displaystyle b}$ است.
• یک عمل دوتایی ${\displaystyle \circ }$ روی ${\displaystyle hom(C)}$ که به آن ترکیب می‌گوییم. به گونه ایکه برای هر سه سازه

${\displaystyle a,b,c\in Ob(C)}$ داریم ${\displaystyle \circ :hom(b,c)\times hom(a,b)\to hom(a,c)}$ و این عمل خواص زیر را دارد:

۱. شرکت پذیری: اگر ${\displaystyle g:b\to c}$،${\displaystyle f:a\to b}$ و ${\displaystyle h:c\to d}$ آنگاه: ${\displaystyle h\circ (g\circ f)=(h\circ g)\circ f}$

۲. همانی: برای هر ${\displaystyle x\in Ob(C)}$، یک پیکان ${\displaystyle 1_{x}:x\to x}$ به نام ریختار همانی موجود است که: برای هر ریختار ${\displaystyle f:a\to b}$ داریم: ${\displaystyle 1_{b}\circ f=f=f\circ 1_{a}}$.

برای آسانی در نوشتار معمولاً نویسه ${\displaystyle f\circ g}$ را به صورت ${\displaystyle fg}$ خلاصه می‌کنیم.

نمونه‌ها

• رده ${\displaystyle Set}$ که سازه‌های آن مجموعه‌ها و پیکانهای آن تابعهای میان مجموعه‌ها هستند. به زبان دیگر: ${\displaystyle S\in Set}$ یک مجموعه و ${\displaystyle f\in hom(S,T)}$ یک تابع از مجموعه ${\displaystyle S}$ به مجموعه ${\displaystyle T}$ است.
• رده ${\displaystyle Gr}$ که سازه‌ها یا اشیاء آن گروه‌ها و پیکانهای یا ریختارهای آن همریختی‌های گروهی هستند. به زبان دیگر: ${\displaystyle G\in Gr}$ یک گروه و ${\displaystyle f\in hom(G,H)}$ یک همریختی گروهی ${\displaystyle f:G\to H}$ است.
• رده ${\displaystyle Ring}$ که سازه‌ها یا اشیاء آن حلقه‌ها و پیکانهای یا ریختارهای آن همریختی‌های حلقه‌ای هستند. به زبان دیگر: ${\displaystyle R\in Ring}$ یک حلقه و ${\displaystyle f\in hom(R,S)}$ یک همریختی حلقه‌ای ${\displaystyle f:R\to S}$ است.
• رده ${\displaystyle Top}$ که سازه‌های آن فضاهای توپولوژیک و پیکانها، تابع‌های پیوسته میان فضاهای توپولوژیک می‌باشند.

گونه‌های ریختارها

یک ریختار (یا پیکان) ${\displaystyle f:a\to b}$ را:

• یک به یک گوییم اگر از ${\displaystyle fg_{1}=fg_{2}}$ برای همه ریختارهای ${\displaystyle g_{1},g_{2}:x\to a}$ نتیجه شود: ${\displaystyle g_{1}=g_{2}}$.
• پوشا گوییم اگر از ${\displaystyle g_{1}f=g_{2}f}$ برای همه ریختارهای ${\displaystyle g_{1},g_{2}:b\to x}$ نتیجه شود: ${\displaystyle g_{1}=g_{2}}$.
• دوسو گوییم اگر یک به یک و پوشا باشد.
• یکریختی گوییم اگر دارای وارون باشد یعنی یک ریختار ${\displaystyle g:b\to a}$ وجود داشته باشد که:

${\displaystyle fg=1_{b}}$ و ${\displaystyle gf=1_{a}}$.

جستارهای وابسته

• عملگر

منابع

• Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag,
• J. Adámek, H. Herrlich, G.E. Strecker: Abstract and concrete categories. The Joy of Cats. John Wiley, 1990.