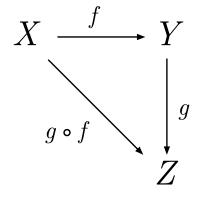ریخت

در بسیاری از شاخه‌ها ریاضیات، ریخت (به انگلیسی: Morphism) (پیکان) اشاره به یک نگاشت حافظِ ساختار از یک ساختار ریاضی به ساختاری دیگر دارد. مفهوم ریخت، در بیشتر ریاضیات معاصر به چشم می خورد. پیکان‌ها در نظریه مجموعه ها، توابع؛ در جبر خطی، نگاشت‌های خطی؛ در نظریه گروه ها، هم‌ریختی‌های گروهی، و در توپولوژی، توابع پیوسته هستند و غیره.

در نظریه رسته‌ها، پیکان مفهوم بسیار مشابهیست، که تا حدودی مجردتر از ریخت در جاهای دیگر ریاضیست: اشیاء ریاضی که ریخت در نظریه رسته‌ها با آن سروکار دارد لزوماً مجموعه نیستند و ریخت بین آنها ممکن است عامل تر از نگاشت های معمولی باشد.

مطالعه پیکان‌ها و اشیاء که به روی آنها تعریف شده‌اند، ایده‌ای اساسی در نظریه رسته هاست. بسیاری از اصطلاحات مربوط به ریخت‌ها و همچنین شهود پشتشان، از رسته‌های ملموس می‌آیند، که در آنها اشیاء به سادگی مجموعه‌هایی با ساختار اضافی و ریخت‌ها، توابع حافظ ساختارند.

تعریف

رسته C شامل دو کلاس است: یکی از اشیاء و دیگر از ریخت‌ها.

به هر ریخت، دو شئ منتسب می‌شود: مبدأ و مقصد (هدف).

برای بسیاری از رسته‌های رایج، اشیاء مجموعه (معمولاً با ساختاری بیشتر) بوده و ریخت‌ها، توابع از یک شئ به شئ دیگر هستند؛ بنابراین مبدأ و مقصدِ یک ریخت، اغلب به ترتیب با نام‌های دامنه و هم-دامنه شناخته می‌شوند.

یک ریخت f با مرجع X و هدف Y را به صورت f: X → Y می‌نویسند. در نتیجه یک ریخت توسط یک پیکان از مبدأ آن به مقصدش نمایش داده می‌شود.

ریخت‌ها مجهز به یک عمل دودویی جزئی به نام ترکیب هستند. ترکیب دو ریخت f و g تعریف می‌شود اگر و تنها اگر مقصد f، مبدأ g باشد، و با g∘f نمایش می‌دهند. مبدأ g∘f مبدأ f و مقصد g∘f، مقصد g است. ترکیب، دو اصل موضوعه را ارضاء می‌کند:

همانی
برای هر شئ X، ریخت idX: X → X به نام ریخت همانی در X وجود دارد به طوری که برای هر ریخت f: A → B، داریم‏ idB ∘ f = f = f ∘ idA ‎.
شرکت پذیری

‏ h ∘ (g ∘ f) = (h ∘ g) ∘ f ‎ هر زمان که عملیات ترکیب سازی تعریف شدنی باشد، یعنی وقتی که مقصد f، مبدأ g بوده و مقصد g، مبدأ h باشد. برای یک رسته محسوس (یعنی که اشیاء اش مجموعه‌های با ساختار اضافه و پیکان‌هایش، نگاشت‌های حافظ ساختارند) ریخت همانی، همان تابع همانی بوده و ترکیب، همان ترکیب توابع معمولی است؛ لذا شکرت پذیری، نتیجه می‌شود چرا که ترکیب توابع شرکت پذیر است.

ترکیب ریخت‌ها اغلب توسط یک نمودار جابجایی نشان داده می‌شود. برای مثال،

مجموعه تمام ریخت‌های از X به Y را با‏ homC(X,Y)‎ یا به ساده‌تر، با‏ hom(X, Y)‎ نشان می‌دهند و به آن و به نام هوم-سِتِ بین X و Y می‌گویند. برخی مؤلفین، می‌نویسند‏ MorC(X,Y)‎،‏ Mor(X,Y)‎ یا ‏ C(XY)‎. توجه داشته باشید که هوم-سِت، اسمی نامناسب است؛ چرا که خانواده ریخت‌ها لزوماً مجموعه نیست. یک رسته را که در آن‏ hom(X,Y)‎ بازای همه اشیاء X و Y، مجموعه است، موضعاَ کوچک می‌گویند.

توجه داشته باشید که دامنه و هم-دامنه در واقع بخشی از اطلاعات تعیین کننده یک ریخت است. برای مثال در رسته مجموعه‌ها، که در آن ریخت‌ها توابعند، دو تابع ممکن است به عنوان مجموعه‌ای از زوج‌های مرتب یکسان باشند (ممکن است دارای بُرد یکسانی باشند) در حالی که هم-دامنه‌های متفاوتی دارند. در نتیجه بسیاری از مؤلفین نیاز دارند که هوم-کلاس‌های ‏ hom(X,Y)‎ مجزا باشند. در عمل این یک مشکل نیست چرا که اگر این گسستگی برقرار نباشد، آنگاه می‌توان مطمئن شد که با اضافه کردن دامنه و هم-دامنه به ریخت‌ها (به عبارتی، به عنوان مولفه‌های دوم و سوم از یک سه تایی مرتب) این مسئله برقرار می‌شود.

مثال

برای نمونه‌های بیشتر، مدخل نظریه رسته‌ها را ببینید.

یادداشت‌ها

    منابع
      • Jacobson, Nathan (2009), Basic algebra, 2 (2nd ed.), Dover, ISBN 978-0-486-47187-7.
      • Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and Concrete Categories (PDF). John Wiley & Sons. ISBN 0-471-60922-6. Now available as free on-line edition (4.2MB PDF).

      پیوند به بیرون
      This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.