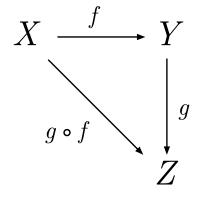تبدیل طبیعی

در نظریه رسته‌ها، شاخه‌ای از ریاضیات، یک تبدیل طبیعی راهی برای تبدیل یک تابعگون به یکی دیگر فراهم می‌کند در حالی که به ساختار داخلی (به عنوان مثال ترکیب پیکان‌ها) رسته‌های درگیر، احترام می‌گذارد. از این رو یک تبدیل طبیعی می‌تواند به عنوان یک «پیکان از تابعگون‌ها» تلقی شود. در واقع این شهود می‌تواند به جهت تعریف رسته‌های تابعگون‌ها صوری بندی شود. تبدیلات طبیعی، پس از رسته‌ها و تابعگون‌ها، یکی از اساسی‌ترین مفاهیم نظریه رسته‌ها هستند و در عمدهٔ کاربردهای آن، ظاهر می‌شوند.

تعریف

اگر F و G تابعگون‌هایی بین رسته‌های C و D باشند، در آن صورت، یک تبدیل طبیعی η از F به G خانواده‌ای از پیکان هاست دو شرط را ارضاء می‌کند.

  1. تبدیل طبیعی باید به هر شیء X در C یک فِلِش ‏ηX: F(X) → G(X) ‎ بین اشیاء D نظیر کند. پیکانِ ηX، مولفه ن η در X نامیده می‌شود.
  2. مؤلفه‌ها باید به گونه‌ای باشد که برای هر پیکان f:X → Y داشته باشیم:

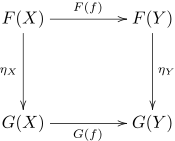
معادلهٔ اخیر را می‌توان به راحتی با نمودار جابجایی زیر تبیین کرد:

اگر F و G پادوردا باشند، پیکان‌های افقی در این نمودار، بر عکس می‌شوند. اگر η یک تبدیل طبیعی از F به G باشند، همچنین می‌توان نوشت η: F → G یا η: F ⇒ G. این را همچنین می‌توان اینطور بیان کرد که خانوادهٔ پیکانهای ‏ ηX: F(X) → G(X) ‎ در X طبیعی است.

اگر برای هر شئ X در C، پیکان ηX یک یکریختی باشد، یک‌ریختی در D باشد، در آنصورت η را یک یکریختی طبیعی (یا گاهی هم‌ارزی طبیعی یا یکریختی تابعگون‌ها) می‌گویند. دو تابعگون F و G را به طور طبیعی یکریخت یا به‌طور ساده‌تر، یکریخت گویند اگر یک یکریختی از F به G وجود داشته باشد.

یک تبدیل طبیعی η از F به G، عملاً یک خانواده ‏ ηX: F(X) → G(X) ‎ از پیکان هاست. بنابراین یک تبدیل طبیعی، یک تبدیل غیرطبیعی است که ηY ∘ F(f) = G(f) ∘ ηX برای هر پیکان f: X → Y. طبیعی ساز η، که با‏ nat(η) ‎ نشان می‌دهند، بزرگترین زیر-رسته از C شامل تمام اشیاء از C که η به یک تبدیل طبیعی تحدید می‌شود.

مثال

دترمینان

برای حلقه‌های جابجایی R و S با همریختی ‏ f: R → S ‎، گروه‌های متناظر متشکل از ماتریس‌های n × n وارون پذیر ‏ GLn(R)‎ و ‏ GLn(S)‎، یک همریختی ‏ GLn(f)‎ را به ارث می‌برند که با استفاده از f به روی هر مولفه از ماتریس به دست می‌آیند. به طور مشابه، f به یک همریختی گروهی f*: R* → S تحدید می شودکه در آن *R نشان دهنده گروه همانی‌های R است. در واقع ‏ GLn ‎ و * تابعگون‌هایی از CRing به Grp هستند. دترمینان روی گروه ‏ GLn(R)‎ را که با ‏ detR ‎ نشان می‌دهیم، یک همریختی گروهی از ‏ GLn(R)‎ به *R است. به علاوه با توجه به اینکه دترمینان روی تمام حلقه‌ها به طور یکسانی تعریف می‌شود، داریم: ‏ f* ∘ detR = detS ∘ GLn(f)‎. این نکته، باعث می‌شود که دترمینان، یک تبدیل طبیعی از ‏ GLn ‎ به * محسوب شود.

لم یوندا

اگر X یک شی از یک رسته موضعاَ کوچک C باشد، در آن صورت، تابع یک تابعگون هموردای FX: C → Set تعریف می‌کند. این تابعگون، نمایش پذیر خوانده می‌شود (به طور کلی یک تابعگون نمایش پذیر، هر تابعگونیست که برای X ای مناسب، به طوری طبیعی یکریخت با تابعگون فوق است). تبدیلات طبیعی از یک تابعگون نمایش پذیر به یک تابعگون دلخواه F: C → Set، کاملاً قابل شناسایی و به سادگی توصیف پذیرند. این، محتوای لم یونداست.

یادداشت‌های تاریخی

گفته شده که ساندرز مک لین، یکی از بنیانگذاران نظریهٔ رسته‌ها، گفته است: «من رسته‌ها را برای مطالعهٔ تابعگون‌ها ابداع نکردم؛ آنها را برای مطالعه تبدیلات طبیعی ابداع نمودم.»[1] همان‌طور مطالعهٔ گروه‌ها بدون مطالعهٔ همریختی‌ها کامل نیست، مطالعهٔ رسته‌ها بدون مطالعهٔ تابعگون‌ها ناکامل است. دلیل اظهار نظر مک لین این است که مطالعه تابعگون‌ها، بدون مطالعهٔ تبدیلات طبیعی، به خودی خود کامل نیست.

پیش زمینهٔ سخن مک لین، نظریهٔ اصل موضوعه‌ای همولوژی‌ها بود. می‌توان نشان داد که روش‌های مختلف ساخت همولوژی، برهم منطبق اند: به عنوان مثال در مورد یک مجتمع سادکی (به انگلیسی: simplicial complex)، گروه‌هایی که مستقیماً تعریف شده‌اند، با آنهایی که از نظریهٔ تکین هستند، یکریخت خواهند بود. آنچه را که نمی‌توان بدون زبان تبدیلات طبیعی به راحتی تبیین کرد، این است که چگونه گروه‌های همولوژی با پیکان‌های بین اشیاء، سازگارند، و اینکه چطور دو تئوری همولوژی معادل، نه تنها گروه‌های همولوژی یکسانی دارند، بلکه مورفیزم‌های یکسانی بین آن گروه‌ها نیز دارند.

منابع
  1. (Mac Lane 1998, §I.4)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.