هم‌ریختی

در جبر مجرد، هم‌ریختی یا همومورفیسم (به انگلیسی: Homomorphism)، نگاشتی است بین دو ساختار جبری (مانند دو گروه، حلقه یا فضای برداری). هر هم‌ریختی که یک به یک و پوشا باشد را یک‌ریختی می‌نامیم. کلمهٔ همومرفیسم در زبان یونان باستان از کلمهٔ ὁμός (homos) به معنی «یکسان» و μορφή (morphe) به معنی «ریخت» یا «شکل» گرفته شده‌است.

هم‌ریختی فضاهای برداری را نگاشت‌های خطی، و مطالعه‌شان را جبر خطی گویند.

مفهوم هم‌ریختی تحت عنوان ریخت، به ساختارهای بسیار دیگری که بنیان مجموعه ای ندارند یا حتی جبری نیستند نیز تعمیم یافته‌است. این تعمیم نقطه آغازین نظریه رسته‌هاست.

هم‌ریختی می‌تواند یک‌ریختی، درون‌ریختی، خودریختی و … نیز باشد. (ادامه مقاله را ببینید). هر کدام از این‌ها را می‌توان به گونه‌ای تعریف کرد که به هر کلاس از ریخت‌ها نیز تعمیم یابد.

تعریف

یک هم‌ریختی، نگاشتی بین دو ساختار جبری از یک سنخ می‌باشد که عملیات ساختارها را حفظ می‌کند؛ یعنی نگاشتی چون ${\displaystyle f\colon A\rightarrow B}$ بین دو مجموعه ${\displaystyle A,B}$ که هردو به یک ساختار و در نتیجه به یک عملگر مجهز باشند، چنان‌که اگر ${\displaystyle \cdot }$ عملی روی این ساختار باشد (در اینجا برای ساده‌سازی فرض می‌کنیم که عملگر مد نظر یک عملگر دوتاییست)، آنگاه برای هر ${\displaystyle x,y}$ در ${\displaystyle A}$[یادداشت 1] داریم:

${\displaystyle f(x\cdot y)=f(x)\cdot f(y)}$

می‌گویند ${\displaystyle f}$ عملیات را حفظ می‌کند یا با آن سازگاری دارد.

به‌طور صوری، نگاشتی چون ${\displaystyle f\colon A\rightarrow B}$ یک عملیات ${\displaystyle k}$-تایی چون ${\displaystyle \mu }$ را که بر روی هردوی ${\displaystyle A}$ و ${\displaystyle B}$ تعریف شده‌است، حافظ ساختار است اگر برای تمام ${\displaystyle x,y}$ در ${\displaystyle A}$ داشته باشیم:

${\displaystyle f(\mu _{A}(a_{1},\ldots ,a_{k}))=\mu _{B}(f(a_{1}),\ldots ,f(a_{k})),}$

عملیاتی که باید تحت هم‌ریختی‌ها حفظ شوند شامل عملیات ۰-تایی، یعنی ثوابت نیز می‌شود. زمانی که ساختارهای مذکور عنصر همانی داشته باشند، عنصر همانی دامنه باید به عنصر همانی متناظر با آن در هم‌دامنه نگاشته شود.

به عنوان مثال:

• یک هم‌ریختی نیم‌گروهی نگاشتی بین نیم‌گروه‌هاست که عمل نیم‌گروه را حفظ می‌کند.
• یک هم‌ریختی مونوئیدی نگاشتی بین مونوئیدهاست که عمل مونوئید را حفظ کرده و عنصر همانی مونوئید اول را به عمل دوتایی مونوئید دومو می‌نگارد (درینجا عنصر همانی عمل ۰-تاییست).
• یک هم‌ریختی گروهی، نگاشتی بین گروه‌هاست که عمل گروهی را حفظ می‌کند. این هم‌ریختی منجر به این می‌شود که عنصر همانی گروه اول به عنصر همانی گروه دوم نگاشته شده و عنصر معکوس یک عضو از گروه اول به معکوس تصویر آن عضو نگاشته می‌شود؛ لذا هم‌ریختی نیم‌گروهی بین گروه‌ها لزوماً یک هم‌ریختی گروهیست.
• یک هم‌ریختی حلقه ای نگاشتی بین حلقه‌هاست که جمع حلقه ای، ضرب حلقه ای و عنصر همانی ضربی حلقه را حفظ می‌کند. این که آیا همانی ضربی حفظ می‌شود بستگی به تعریف حلقه مورد استفاده دارد. اگر همانی ضربی حفظ نشود، به تعریف هم‌ریختی رانگ rng می‌رسیم.
• نگاشت خطی هم‌ریختی ای از فضاهای برداریست؛ یعنی هم‌ریختی گروهی بین فضاهای برداری که ساختار گروه آبلی و ضرب اسکالر را حفظ می‌کند.
• یک هم‌ریختی مدولی که به آن نگاشت خطی بین مدول‌ها نیز گفته می‌شود به‌طور مشابه تعریف می‌شود.
• یک هم‌ریختی جبری نگاشتی است که عملیات جبری را حفظ می‌کند.

ممکن است یک ساختار جبری بیش از یک عمل داشته باشد و برای حفظ هر کدام از آن عمل‌ها نیاز به یک هم‌ریختیست؛ لذا نگاشتی که فقط برخی از آن عمل‌ها را حفظ کند هم‌ریختی ساخار نیست، بلکه صرفاً هم ریختی آن ساختار تحت عمل‌های حفظ شده می‌باشد. به عنوان مثال، نگاشتی بین مونوئیدها که عمل مونوئید را حفظ کرده اما عنصر همانی را حفظ نکند یک هم‌ریختی مونوئیدی نیست، بلکه صرفاً یک هم‌ریختی نیم‌گروهیست.

مثال‌ها

هم‌ریختی مونوئیدی ${\displaystyle f}$ از مونوئید ${\displaystyle \color {green}(\mathbf {N} ,+,\,0)}$ به مونوئید ${\displaystyle \color {red}(\mathbf {N} ,\times ,0)}$ که به صورت ${\displaystyle f(x)=2^{x}}$ تعریف شده‌است. این هم‌ریختی یک به یک است اما پوشا نیست.

اعداد حقیقی تشکیل یک حلقه می‌دهند که در آن هم عمل جمع وجود دارد و هم عمل ضرب. مجموعه تمام ماتریس‌های ${\displaystyle 2\times 2}$ نیز تحت اعمال جمع و ضرب ماتریسی تشکیل یک حلقه می‌دهند. اگر ما تابعی بین این دو حلقه (اعداد حقیقی و ماتریس‌های ${\displaystyle 2\times 2}$) به صورت زیر تعریف کنیم:

${\displaystyle f(r)={\begin{pmatrix}r&0\\0&r\end{pmatrix}}}$

که در آن ${\displaystyle r}$ یک عدد حقیقیست، آنگاه ${\displaystyle f}$ هم‌ریختی بین حلقه‌ها خواهد بود، چرا که ${\displaystyle f}$ هم جمع را حفظ می‌کند:

${\displaystyle f(r+s)={\begin{pmatrix}r+s&0\\0&r+s\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}+{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)+f(s)}$

هم ضرب را:

${\displaystyle f(rs)={\begin{pmatrix}rs&0\\0&rs\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)\,f(s).}$

به عنوان مثالی دیگر، اعداد مختلط ناصفر را در نظر بگیرید، این اعداد مانند اعداد حقیقی ناصفر تحت عمل ضرب تشکیل یک گروه می‌دهند (صفر از هردوی این گروه‌ها باید حذف شود چرا که معکوس ضربی ندارد، که از شرایط ضروری گروه‌هاست). تابعی مثل ${\displaystyle f}$ از اعداد مختلط ناصفر به اعداد حقیقی ناصفر به صورت زیر تعریف می‌کنیم:

${\displaystyle f(z)=|z|.}$

یعنی ${\displaystyle f(z)}$ قدرمطلق عدد مختلط ${\displaystyle z}$ است. آنگاه ${\displaystyle f}$ هم‌ریختی گروه‌هاست، چرا که ضرب را حفظ می‌کند:

${\displaystyle f(z_{1}z_{2})=|z_{1}z_{2}|=|z_{1}||z_{2}|=f(z_{1})f(z_{2}).}$

توجه کنید که ${\displaystyle f}$ را نمی‌توان به هم‌ریختی حلقه ای بسط داد (هم‌ریختی حلقه ای از اعداد مختلط به اعداد حقیقی)، چرا که جمع را حفظ نمی‌کند:

${\displaystyle |z_{1}+z_{2}|\neq |z_{1}|+|z_{2}|.}$

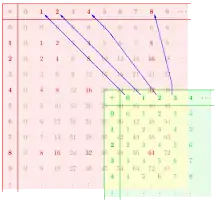
به عنوان مثالی دیگر، درون تصویر نمودار هم‌ریختی ${\displaystyle f}$ی از مونوئید ${\displaystyle (\mathbf {N} ,+,\,0)}$ به ${\displaystyle (\mathbf {N} ,\times ,0)}$ نشان داده شده. به علت مختلف بودن اعمال دوتایی این دو ساختار، خاصیت هم‌ریختی ${\displaystyle f}$ به صورت ${\displaystyle f(x+y)=f(x)\times f(y)}$ نشان داده می‌شود و داریم ${\displaystyle f(0)=1}$.

یک جبر ترکیبیاتی ${\displaystyle A}$ روی میدان ${\displaystyle F}$ که به فرم مربعی باشد را نرم نامیده که به صورت ${\displaystyle N\colon A\rightarrow F}$ است و یک هم‌ریختی گروهی از گروه ضربی ${\displaystyle A}$ به گروه ضربی ${\displaystyle F}$ می‌باشد.

هسته

هر هم‌ریختی ${\displaystyle f\colon X\rightarrow Y}$ یک رابطه هم‌ارزی ${\displaystyle \sim }$ را روی ${\displaystyle X}$ بدین صورت تعریف می‌کند که ${\displaystyle a\sim b}$ اگر و تنها اگر ${\displaystyle f(a)=f(b)}$. رابطه ${\displaystyle \sim }$ را هسته‌ی ${\displaystyle f}$ گویند. این رابطه، یک رابطه هم‌ارزی روی ${\displaystyle X}$ است. مجموعه خارج قسمتی ${\displaystyle X/\sim }$ را می‌توان به گونه ای طبیعی، با تعریف عملیات بین دسته‌های هم‌ارزی ${\displaystyle [x]*[y]=[x*y]}$ مجهز به همان ساختار کرد. درین صورت، تصویر ${\displaystyle X}$ در ${\displaystyle Y}$ تحت هم‌ریختی ${\displaystyle f}$ لزوماً یک‌ریخت با ${\displaystyle X/\sim }$ می‌باشد، حقیقت اخیر یکی از قضایای یک ریختیست. زمانی که ساختار جبری مد نظر برای برخی از عمل‌ها گروه باشد، کلاس هم‌ارزی ${\displaystyle K}$ مربوط به عنصر همانی این عمل برای تعیین و مشخصه سازی رابطه کافیست. در این صورت، خارج قسمت رابطه هم‌ارزی به صورت ${\displaystyle X/K}$ نمایش داده می‌شود (به صورت "${\displaystyle X}$ به هنگ ${\displaystyle K}$" یا "${\displaystyle X}$ به پیمانه ${\displaystyle K}$" خوانده می‌شود). همچنین در این صورت، بیشتر به ${\displaystyle K}$ هسته ${\displaystyle f}$ می‌گویند تا ${\displaystyle \sim }$. هسته‌های هم‌ریختی از نوع یک ساختار جبری داده شده، طبیعتاً خود مجهز به ساختاریست. این ساختارِ مربوط به هسته، هم سنخ با ساختار جبری است که بر روی آن کار می‌کنیم (صورت و مخرج‌های کسر)، مثلاً اگر صورت و مخرج کسر از نوع گروه آبلی، فضای برداری یا مدول باشد خارج قسمت ما نیز از همین نوع است، اما به خاطر ویژگی‌های خاصی که دارد معمولاً اگر هسته یک هم‌ریختی گروهی باشد به آن زیر گروه نرمال و اگر هسته هم‌ریختی حلقه ای باشد بدان ایده‌آل گویند (در مورد حلقه‌های ناجابجایی، هسته‌ها ایده‌آل‌های دوسویه هستند).

هم‌ریختی‌های خاص

چندین نوع از هم‌ریختی‌ها برای خود نام‌های خاصی دارند، که تعمیمشان به ریخت‌های نظریه رسته‌ها نیز از همین نام‌ها بهره می‌برند.

یک‌ریختی

یک یک‌ریختی بین دو ساختار جبری هم‌سنخ را اغلب به صورت هم‌ریختی دوسویه تعریف می‌کنند.[1]^:134[2]^:28

در بستر عام تر نظریه رسته‌ها، یک‌ریختی به صورت ریخت تعریف می‌شود، ریختی که دارای معکوسیست که خود آن هم ریخت باشد. در مورد ساختارهای جبری خاص، این دو تعریف معادل هستند، گرچه که ممکن است برای ساختارهای غیر جبری که دارای مجموعه زیرین باشند این دو تعریف متفاوت باشد.

به‌طور دقیق تر اگر:

${\displaystyle f\colon A\rightarrow B}$

یک (هم) ریخت باشد، دارای معکوس است اگر وجود داشته باشد:

${\displaystyle g\colon B\rightarrow A}$

چنان‌که:

${\displaystyle f\circ g=\operatorname {Id} _{B}\qquad ,\qquad g\circ f=\operatorname {Id} _{A}.}$

اگر ${\displaystyle A}$ و ${\displaystyle B}$ دارای مجموعه زیرین باشند و ${\displaystyle f\colon A\rightarrow B}$ دارای معکوس ${\displaystyle g}$ باشد، آنگاه ${\displaystyle f}$ دوسویه است. در حقیقت ${\displaystyle f}$ یک به یک است، چرا که ${\displaystyle f(x)=f(y)}$ نتیجه می‌دهد ${\displaystyle x=g(f(x))=g(f(y))=y}$ و ${\displaystyle f}$ پوشاست چرا که برای هر ${\displaystyle x}$ در ${\displaystyle B}$ داریم ${\displaystyle x=f(g(x))}$ و ${\displaystyle x}$ تصویر عنصری از ${\displaystyle A}$ است.

برعکس، اگر ${\displaystyle f\colon A\rightarrow B}$ یک هم‌ریختی دو سویه بین ساختارهای جبری باشد، فرض کنید ${\displaystyle g\colon B\rightarrow A}$ نگاشتی باشد چنان‌که ${\displaystyle g(y)}$ عنصر منحصر به فردی چون ${\displaystyle x}$ از ${\displaystyle A}$ بوده چنان‌که ${\displaystyle f(x)=y}$. در نتیجه داریم ${\displaystyle f\circ g=\operatorname {Id} _{B}}$ و ${\displaystyle g\circ f=\operatorname {Id} _{A}}$، و تنها چیزی که باقی می‌ماند این است که نشان دهیم ${\displaystyle g}$ یک هم‌ریختیست. اگر ${\displaystyle *}$ یک عمل دوتایی این ساختار باشد، برای هر جفت ${\displaystyle x,y}$ از عناصر ${\displaystyle B}$ داریم:

${\displaystyle g(x*_{B}y)=g(f(g(x))*_{B}f(g(y)))=g(f(g(x)*_{A}g(y)))=g(x)*_{A}g(y),}$

و لذا ${\displaystyle g}$ با ${\displaystyle *}$ سازگار خواهد بود. اثبات آن برای هر عمل چندتایی دیگر هم مشابه عمل دوتاییست، و از آن نتیجه می‌گیریم که ${\displaystyle g}$ یک هم‌ریختیست.

این اثبات برای ساختارهای غیر جبری کار نمی‌کند. به عنوان مثال، برای فضاهای توپولوژیکی، ریخت را نگاشت پیوسته گویند، و معکوس نگاشت پیوسته دو سویه لزوماً پیوسته نیست. یک‌ریختی در فضاهای توپولوژی را همسان‌ریختی یا نگاشت دوپیوسته (نگاشتی که هم خودش و هم معکوسش پیوسته باشند) گویند.

درون‌ریختی

یک درون‌ریختی، هم‌ریختیست که دامنه اش برابر با هم دامنه‌اش باشد، یا به‌طور کلی تر ریختی که منبع آن با هدفش برابر باشد.[1]^:135

درون‌ریختی‌های یک ساختار جبری، یا شیئی از یک رسته تحت عمل ترکیب تشکیل مونوئید می‌دهد.

درون‌ریختی‌های یک فضای برداری یا یک مدول تشکیل یک حلقه می‌دهد. در حالتی که در بستر فضاهای برداری یا مدول‌های آزاد متناهی بعد کار می‌کنیم، انتخاب پایه، یک‌ریختی حلقه‌ای بین حلقه درون‌ریختی‌ها و حلقه ماتریس‌های مربعی هم بعد القاء می‌کند.

خودریختی

یک خودریختی، درون‌ریختیست که علاوه بر درون‌ریختی، یک‌ریختی نیز می‌باشد.[1]^:135

خودریختی‌های یک ساختار جبری یا یک شیء از یک رسته، تحت عمل ترکیب، تشکیل گروه می‌دهد که به آن گروه خودریختی‌های آن ساختار می‌گوییم.

بسیاری از گروه‌هایی که بر روی آن‌ها نامی قرار داده شده، خود گروه خودریختی از یک ساختار جبری اند. به عنوان مثال، گروه خطی عمومی ${\displaystyle GL_{n}(k)}$ گروه خودریختی فضاهای برداری ${\displaystyle n}$ بعدی روی یک میدان ${\displaystyle k}$ می‌باشد.

گروه‌های خودریختی میدان‌ها توسط اواریسته گالوا به منظور مطالعه ریشه چند جمله‌ای‌ها معرفی شدند و اکنون پایه نظریه گالوا می‌باشند.

تک‌ریختی

برای ساختارهای جبری، تک‌ریختی‌ها عمدتاً به صورت هم‌ریختی‌های یک به یک تعریف می‌شوند.[1]^:134[2]^:29

در حالت کلی تر، در نظریه رسته‌ها، یک تک‌ریختی به صورت ریختی تعریف می‌شود که خاصیت چپ حذف شدنی دارد.[3] این بدین معناست که (هم) ریختی ${\displaystyle f\colon A\rightarrow B}$ تک ریختیست اگر برای هر جفت ${\displaystyle f,g}$ از ریخت‌ها از هر شیء درون رسته ${\displaystyle C}$ به شیء ${\displaystyle A}$ از ${\displaystyle f\circ g=f\circ h}$ نتیجه بگیریم که ${\displaystyle g=h}$.

بروریختی

در جبر، بروریختی‌ها را اغلب به صورت هم‌ریختی‌های پوشا تعریف می‌کنند.[1]^:134[2]^:43 از سوی دیگر، در نظریه رسته‌ها، بروریختی‌ها را به صورت ریخت‌هایی تعریف می‌کنند که خاصیت راست حذف شدنی دارند.[3] این بدین معناست که (هم) ریختی ${\displaystyle f\colon A\rightarrow B}$ بروریختیست اگر برای هر جفت ${\displaystyle g,h}$ از ریخت‌هایی که از شیء ${\displaystyle B}$ به هر شیء دیگری از رسته ${\displaystyle C}$ می‌روند از ${\displaystyle g\circ f=h\circ f}$ نتیجه بگیریم که ${\displaystyle g=h}$.

یادداشت‌ها

1. اغلب، اما نه همیشه، حتی زمانی که دو مجموعه مجهز به دو ساختار متفاوت، و در نتیجه دو عمل متفاوت باشند، عملیات مربوط به هر دو مجموعه مذکور را با یک نماد نمایش می‌دهند.

ارجاعات

1. Birkhoff, Garrett (1967) [1940], Lattice theory, American Mathematical Society Colloquium Publications, 25 (3rd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1025-5, MR 0598630
2. Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
3. Mac Lane, Saunders (1971). Categories for the Working Mathematician. Graduate Texts in Mathematics. 5. Springer-Verlag. Exercise 4 in section I.5. ISBN 0-387-90036-5. Zbl 0232.18001.

• مشارکت‌کنندگان ویکی‌پدیا. «Homomorphism». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۹ سپتامبر ۲۰۱۹.

منابع

• Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
• Mac Lane, Saunders (1971), Categories for the Working Mathematician, Graduate Texts in Mathematics, 5, Springer-Verlag, ISBN 0-387-90036-5, Zbl 0232.18001
• Fraleigh, John B.; Katz, Victor J. (2003), A First Course in Abstract Algebra, Addison-Wesley, ISBN 978-1-292-02496-7