زاویههای اویلر
زاویههای اویلر سه زاویهای هستند که توسط لئونارد اویلر برای توصیف جهتگیری یک جسم صلب نسبت به یک سیستم مختصات ثابت معرفی شدهاند.[1] این زاویهها در فیزیک میتوانند نمایانگر جهتگیری یک چارچوب مرجع متحرک باشند یا در جبر خطی 3 بعدی این زاویهها جهت گیری یک پایه را نشان میدهند.
زاویههای اویلر را می توان با هندسه ابتدایی یا با ترکیب چرخشها تعریف کرد. تعریف هندسی نشان می دهد که سه دوران ابتدایی تشکیل شده (دوران حول محورهای یک سیستم مختصات) همواره برای دستیابی به هر چارچوب هدفی کافی هستند.
سه دوران ابتدایی میتوانند بیرونی (حول محورهای XYZ سیستم مختصات اصلی، که ثابت فرض میشود)، یا درونی (حول محورهای XYZ سیستم مختصات در حال دوران، که با جسم در حال حرکت همبستگی دارد، و پس از هر دوران ابتدایی، جهت گیری آن تغییر میکند).
زاویه های اویلر معمولاً با α ، β ، γ یا φ ، θ ، ψ نشان داده میشوند. نویسندگان مختلف ممکن است از مجموعه محورهای دوران متفاوتی برای تعریف زاویههای اویلر بهره بگیرند یا نامهای مختلف برای همین زاویهها استفاده کنند. بنابراین، در هر بحثی که از زوایای اویلر استفاده میشود ، همواره باید آنها را در ابتدا تعریف نمود.
چنانچه دو قرارداد مختلف برای تعریف محورهای دوران (ذاتی یا بیرونی) را در نظر نگرفته باشیم، دوازده دنباله از محورهای دوران وجود خواهد داشت که به دو گروه تقسیم میشوند:
- زاویه های مناسب اویلر (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)
- زاویه های تایت-برایان (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)
زاویه های تایت-برایان، زاویه های کاردان، زاویه های دریایی، جهت ، ارتفاع، بانک یا pitch, yaw , و roll نیز نامیده میشوند. بعضی اوقات، هر دو نوع دنباله "زاویه های اویلر" خوانده میشوند. در این حالت، توالی گروه اول زاویه های مناسب یا کلاسیک اویلر نامیده میشود.
زاویه های مناسب اویلر

تعریف هندسی
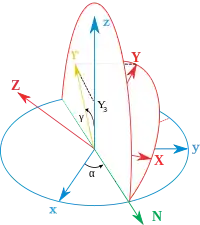
محورهای چارچوب اصلی با x ،y ،z و محورهای چارچوب چرخان با X ،Y ،Z نشان داده میشوند. تعریف هندسی (که گاه به آن استاتیک گفته میشود) با تعریف خط گرهها به عنوان فصل مشترک صفحات xy و XY آغاز میشود (همچنین می توان آن را به عنوان عمود مشترک بر محورهای z و Z تعریف کرد و سپس به عنوان ضرب خارجی N = z Z نوشت). با استفاده از این روش، سه زاویه اویلر را می توان به شرح زیر تعریف کرد:
- (یا ) زاویهی بین محور x و محور N است (قرارداد x- این زاویه را میتوان بین y و N نیز تعریف کزد که در این صورت قرارداد y نامیده میشود).
- (یا ) زاویهی بین محور z و محور Z است.
- (یا ) زاویهی بین محور N و محور X است (قرارداد x).
زاویه های اویلر بین دو چارچوب مرجع فقط در صورتی تعریف میشوند که هر دو چارچوب راستگرد یا هر دو چپگرد باشند.
تعریف با دورانهای ذاتی
دورانهای ذاتی، دورانهای ابتدایی حول محورهای سیستم مختصات XYZ متصل به یک جسم متحرک هستند. محورهای چنین سیستم مختصاتی بعد از هر دوران ابتدایی، جهتگیری خود را تغییر میدهند. سیستم XYZ میچرخد اما xyz ثابت است. با شروع از XYZ و xyz که با هم تداخل دارند، ترکیبی از سه دوران ذاتی را میتوان برای رسیدن به هر جهتگیری هدف برای XYZ مورد استفاده قرار داد.
زاویههای اویلر را می توان با دوران ذاتی تعریف کرد. میتوان تصور کرد که چارچوب دوران XYZ در ابتدا (قبل از انجام دورانهای ابتدایی به اندازهی زاویههای اویلر) با xyz تراز است. ترتیب جهتگیریها را میتوان به شرح زیر نوشت:
- x-y-z یا x0-y0-z0 (اولیه)
- ′x′-y′-z یا x1-y1-z1 (بعد از دوران اول)
- ″x″-y″-z یا x2-y2-z2 (بعد از دوران دوم)
- X-Y-Z یا x3-y3-z3 (نهایی)
برای توالی دورانهای ذکر شده در بالا، خط گره N را به صورت جهت گیری X پس از دوران ابتدایی اول تعریف کرد. لذا N را میتوان با ′x نشان داد. علاوه بر این، چون دوران ابتدایی سوم حول Z انجام میگیرد، جهت Z را تغییر نمیدهد. از این رو Z و ″z بر هم منطبقاند. این به ما امکان میدهد که تعریف زاویههای اویلر را به شرح زیر ساده کنیم:
- α (یا ) دوران حول محور z را نشان میدهد،
- β (یا ) دوران حول محور ′x را نشان میدهد،
- γ (یا ) دوران حول محور ″z را نشان میدهد.
زوایای یک چارچوب معین

یک مسئله معمول یافتن زاویههای اویلر یک چارچوب معین است. سریعترین راه برای بدست آوردن زاویههای اویلر نوشتن سه بردار داده شده به صورت ستون های یک ماتریس و مقایسه آن با عبارت نظری ماتریس است (به جدول بعدی ماتریس مراجعه کنید). لذا سه زاویه اویلر را میتوان محاسبه کرد. با این وجود، میتوان بدون استفاده از جبر ماتریسی و تنها با استفاده از هندسه مقدماتی نیز به همین نتیجه رسید. در اینجا نتایج مربوط به دو قرارداد متداول را ارائه میکنیم:
ZXZ برای زاویه های مناسب اویلر
و ZYX برای Tait – Bryan.
توجه کنید که هر قرارداد دیگری را میتوان فقط با تغییر نام محورها بدست آورد.
زاویههای مناسب اویلر
چارچوبی را با بردارهای واحد ( X ، Y ، Z ) فرض کنید که مختصات آنها مانند نمودار اصلی داده شده است، می توان نوشت:
و از
خواهیم داشت
چون از دو بار تصویر کردن یک بردار واحد بدست آمده است،
را میتوان به صورت مشابه بازسازی کرد یعنی بار اول آن را روی صفحهای که توسط محور z و خط گرهها تعریف میشود، تصویر میکنیم. چون زاویه بین دو صفحه است و ، خواهیم داشت:
و سرانجام با استفاده از تابع کسینوس معکوس،
زاویه های تایت-برایان
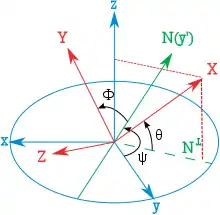
چارچوبی را با بردارهای واحد (X, Y, Z) تصور کنید که مختصات آنها مانند نمودار جدید داده شده است (تزاویه تتا منفی است)، داریم:
همانند مورد پیشین،
داریم
به روشی مشابه مورد پیشین:
عباراتی مشابه روابط سابق بدست میآیند:
تذکرات نهایی
توجه داشته باشید که توابع معکوس سینوس و کسینوس دو مقدار خروجی برای آرگومان ورودی تولید میکنند. در این توصیف هندسی تنها یکی از مقادیر معتبر است. هنگامی که زاویههای اویلر به صورت دنبالهای از دورانها تعریف شوند، تمام مقادیر میتوانند معتبر باشند، اما فقط یکی از خروجیها در دامنه زاویه خواهد بود. این به این خاطر است که توالی دورانها برای رسیدن به چارچوب هدف در صورتی که دامنهها پیشتر تعریف نشده باشند منحصر به فرد نخواهد بود.[2]
برای اهداف محاسباتی، نمایش زاویهها با استفاده از atan2(y, x) مفیدخواهد بود. به عنوان مثال، برای زاویههای مناسب اویلر:
تبدیل به سایر نمایشهای جهتگیری
زاویههای اویلر یک راه نشان دادن جهتگیریها هستند. روشهای دیگری نیز وجود دارند و تبدیل به قراردادهای دیگر یا از قراردادهای دیگر ممکن است. برای توصیف جهتگیریها در یک فضای 3 بعدی اقلیدسی، همیشه به سه پارامتر نیاز است. این 3 پارامتر را با چند روش که زوایای اویلر تنها یکی از آنهاست، ارائه داد. برای اطلاع از سایر روشها نمودارهای SO (3) را ببینید.
رایجترین بازنماییهای جهتگیری عیارتند از ماتریس دوران، زاویه-محور و چهارگانها که پارامترهای اویلر-رودریگز نیز نامیده میشوند و مکانیسم دیگری برای نمایش دورانهای سه بعدی فراهم میکنند. این معادل توضیحات گروه واحد ویژه است.
بیان دوران در فضای سه بعدی به صورت چهارگانهای واحد به جای ماتریس مزایایی دارد:
- جمع کردن دورانها از نظر محاسباتی سریعتر و از نظر عددی پایدارتر است.
- استخراج زاویه و محور دوران سادهتر است.
- درونیابی صریح تر است. به عنوان مثال به SLERP مراجعه کنید.
- چهارگانها برخلاف زاویههای اویلر دچار <a href="https://en.wikipedia.org/wiki/Gimbal_lock%22 rel="mw:ExtLink" data-linkid="209" class="cx-link" title="Gimbal lock">gimbal lock</a>نمیشوند.
محاسبه ماتریس دوران اولین گام برای بدست آوردن دو بازنمایی دیگر است.
ماتریس دوران
هر جهتگیری را میتوان با شروع از یک جهتگیری استاندارد معین و انجام سه دوران ابتدایی بدست آورد. به طور هم ارز، هر ماتریس دوران R را میتوان به صورت ضرب سه ماتریس دوران ابتدایی تجزیه کرد. به عنوان مثال:
یک ماتریس دوران است که میتواند برای نشان دادن ترکیبی از دورانهای بیرونی حول محورهای x, y, z (با همین ترتیب) یا ترکیبی از دورانهای ذاتی حول محورهای z″-y′-x (با همین ترتیب) استفاده شود. با این حال، هر دو تعریف ماتریس دوران اولیه X, Y, Z و ترتیب ضرب آنها بستگی به تعریف کاربر از ماتریس دوران و زاویههای اویلر دارد (به ابهامات تعریف ماتریس دوران مراجعه کنید.) متأسفانه، کاربران در زمینههای مختلف قراردادهای متفاوتی را مورد استفاده قرار دادهاند. جدول زیر مطابق این مجموعه قراردادها ساخته شده است:
- هر ماتریس از طریق ضرب چپ در بردارهای ستونی اعمال میشود (به ابهامات تعریف ماتریس دوران مراجعه کنید)
- هر ماتریس نشان دهندهی یک دوران فعال است (قرار است ماتریس های سازنده و ترسیم شده بر روی مختصات بردارهای تعریف شده در قاب مرجع ثابت اولیه عمل کنند و در نتیجه مختصات یک بردار چرخان را تعریف شده در همان قاب مرجع ارائه دهند).
- منظور از هر ماتریس ، در درجه اول ، ترکیب چرخش های بیرونی (که مربوط به ارزیابی سازنده ماتریس R با ضرب سه ماتریس واقعاً ابتدایی است) و دوم ، ترکیب سه ماتریس غیر ابتدایی است که به صورت جهانی نشان دهنده چرخش های ذاتی است. (در اطراف محورهای قاب مرجع چرخش ، به ترتیب معکوس).
- فریم های مرجع دست راست به تصویب رسیده و از قانون دست راست برای تعیین علامت زاویه ها α ، β ، γ استفاده می شود .
جستارهای وابسته
- پروجکشن سه بعدی
- بازنمایی زاویه-محور
- تبدیل بین چهارگان و زاویه های اویلر
- قضیه چرخش اویلر
- چهارگان
- چهارگانها و دوران مکانی
- روشهای مدل کردن چرخش در سه بعد
- دستگاه مختصات کروی
منابع
- Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) PDF
- Gregory G. Slabaugh, Computing Euler angles from a rotation matrix
کتابشناسی
- Biedenharn, L. C.; Louck, J. D. (1981), Angular Momentum in Quantum Physics, Reading, MA: Addison–Wesley, ISBN 978-0-201-13507-7
- Goldstein, Herbert (1980), Classical Mechanics (2nd ed.), Reading, MA: Addison–Wesley, ISBN 978-0-201-02918-5
- Gray, Andrew (1918), A Treatise on Gyrostatics and Rotational Motion, London: Macmillan (published 2007), ISBN 978-1-4212-5592-7
- Rose, M. E. (1957), Elementary Theory of Angular Momentum, New York, NY: John Wiley & Sons (published 1995), ISBN 978-0-486-68480-2
- Symon, Keith (1971), Mechanics, Reading, MA: Addison-Wesley, ISBN 978-0-201-07392-8
- Landau, L.D.; Lifshitz, E. M. (1996), Mechanics (3rd ed.), Oxford: Butterworth-Heinemann, ISBN 978-0-7506-2896-9
پیوند به بیرون
- Weisstein, Eric W. "Euler Angles". MathWorld.
- An interactive tutorial on Euler angles available at https://www.mecademic.com/resources/Euler-angles/Euler-angles
- EulerAngles – an iOS app for visualizing in 3D the three rotations associated with Euler angles
- Orientation Library – "orilib", a collection of routines for rotation / orientation manipulation, including special tools for crystal orientations
- Online tool to convert rotation matrices available at rotation converter (numerical conversion)
- Online tool to convert symbolic rotation matrices (dead, but still available from the Wayback Machine) symbolic rotation converter
- Rotation, Reflection, and Frame Change: Orthogonal tensors in computational engineering mechanics, IOP Publishing