فرایند همدما
در بحث ترمودینامیک، فرآیند همدما (isothermal process) نوعی از فرآیندهای ترمودینامیکی است که در آن دمای سیستم ثابت میماند : . این حالت
| ترمودینامیک |
|---|
 |
|
زمانی رخ میدهد که سیستم در تماس با یک منبع حرارتی خارجی قرار دارد، و تغییرات سیستم به حدی آرام رخ میدهند که به سیستم این اجازه را میدهند که از طریق مبادلهی گرما، دمای خود را با منبع حرارتی تنظیم کند. در نقطه مقابل، فرآیند بیدررو فرآیندی است که در طی آن سیستم هیچ تبادل گرمایی با محیط پیرامون ندارد().
به طور خلاصه میتوان گفت که در فرآیند همدما :
- (دما)
فقط برای گازهای ایدهآل : (انرژی درونی)
مثالها
فرآیندهای همدما میتوانند در هر سیستمی که به نوعی سامانه تنظیم دما دسترسی دارد، رخ دهند (از جمله: ماشین آلات بسیار پیچیده از لحاظ ساختاری و حتی سلولهای زنده). بعضی از قسمتهای چرخه بعضی از موتورهای گرمایی به صورت همدما (isothermal) انجام می شوند (به عنوان مثال در چرخه کارنو). [1] در تجزیه و تحلیل ترمودینامیکی واکنشهای شیمیایی، معمولاً ابتدا آنچه در شرایط همدما (دما ثابت) اتفاق میافتد را تجزیه و تحلیل کرده و سپس اثر دما را در نظر میگیرند. [2] تغییرات فاز (مانند ذوب شدن یا تبخیر) نیز وقتی در فشار ثابت اتفاق می افتند، فرایندهایی همدما محسوب میشوند.[3] فرآیندهای همدما به وفور مورد استفاده قرار گرفته و به نوعی، یک نقطه شروع در تجزیه و تحلیل فرایندهای پیچیدهتر و غیر همدما هستند.
فرآیندهای همدما در مبحث گازهای ایدهآل مورد توجه ویژهای قرار دارند. این نتیجه قانون دوم ژول است که میگوید: انرژی درونی مقدار ثابتی از یک گاز ایدهآل فقط به دمای آن بستگی دارد. [4] بنابراین، در یک فرآیند همدما، انرژی درونی یک گاز ایدهآل ثابت است. این نتیجه را میتوان از این حقیقت که در یک گاز ایدهآل هیچ نیروی بین مولکولی وجود ندارد، برداشت کرد. [4] توجه داشته باشید که این فقط در مورد گازهای ایدهآل صادق میباشد. در مایعات ، جامدات و گازهای واقعی، انرژی درونی علاوه بر دما (درجه حرارت) به فشار نیز بستگی دارد. [5]
در انقباض همدمای یک گاز، به منظور کاهش حجم و افزایش فشار، کار بر روی سیستم انجام میشود. [4] انجام کار بر روی گاز باعث افزایش انرژی درونی شده که در نهایت به افزایش دما تمایل پیدا خواهد کرد. در این حالت برای ثابت نگهداشتن دمای سیستم، انرژی باید تحت عنوان گرما از سیستم خارج شده و وارد محیط شود. اگر گاز ایدهآل باشد، مقدار انرژی (گرما) وارد شده به محیط، با کار انجام شده بر روی گاز برابر است؛ زیرا انرژی درونی تغییری نمیکند (فقط برای گازهای ایدهآل : ). در فرآیند انبساط همدما، کار انجام شده بر روی محیط، توسط انرژی عرضه شده به سیستم صورت میپذیرد. در هر صورت، با بهکارگیری یک رابط مناسب، تغییر در حجم گاز میتواند کار مکانیکی مفیدی را برای ما انجام دهد. برای جزئیات محاسبات، به بخش محاسبه کار مراجعه کنید.
در یک فرآیند بیدررو، که در آن هیچ گرمایی به داخل گاز وارد نشده و یا از آن خارج نمیشود (زیرا ظرف آن کاملاً عایق است): میباشد. همچنین اگر کاری انجام نشده باشد (برای نمونه : انبساط آزاد)، انرژی درونی سیستم نیز تغییری نخواهد کرد. برای یک گاز ایدهآل، این بدان معنی است که فرآیند علاوه بر بیدررو بودن، همدما نیز هست. [4] بنابراین، صرفا تشخیص یک فرآیند همدمایی، برای تعیین تمامی فرآیندهای دخیل در یک فرآیند منحصر به فرد کافی نیست.
جزئیات یک گاز ایدهآل
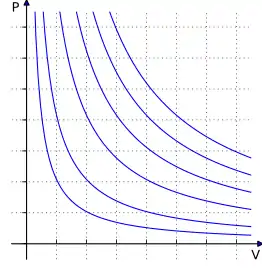
در موارد خاص که قانون بویل [4] بر روی گاز اعمال میشود، اگر گاز در شرایط همدما نگهداری شود، عبارت که بیانگر حاصل ضرب فشار گاز () در حجم آن () است، برابر با مقدار ثابتی خواهد بود که آن مقدار برابر میباشد ( تعداد مولهای گاز موجود و ثابت گازها است). به عبارت دیگر، قانون گازهای ایدهآل () بر روی گاز اعمال می شود. [4] بنابراین میتوان نتیجه گرفت:
دسته منحنیهای تولید شده توسط این معادله، در نمودار شکل 1 نشان داده شده است. هر یک از منحنیهای این نمودار، یک ایزوترم (isotherm) نام دارند. این نمودارها، نمودارهای شاخص هستند و اولین بار توسط جیمز وات و دیگران برای بررسی و نظارت بر کارایی موتورها مورد استفاده قرار گرفتهاند. دمای مربوط به هر منحنی، به ترتیب از پایین سمت چپ به بالا سمت راست افزایش می یابد.
محاسبه کار
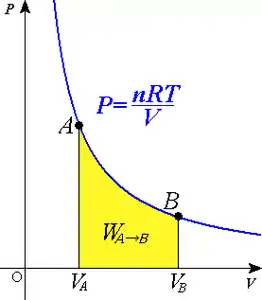
در ترمودینامیک، هنگام تغییر حالت گاز از به ، کار برگشتپذیر انجام میشود. [6]
در یک فرآیند همدمای برگشتپذیر، اندازه کار (مقدار انتگرال نوشته شده در بالا) برابر با سطح زیر منحنی همدمای (فشار- حجم) خواهد بود (شکل 2). با در نظر گرفتن همدمایی فرآیند، بار دیگر میتوان گفت : و عبارت کار را به دست آورد:
طبق قرارداد، کار () به عنوان کار انجام شده بر روی سیستم توسط محیط اطراف آن تعریف میشود. به عنوان مثال اگر سیستم (گاز) منقبض شود، کار مثبت است و انرژی درونی سیستم افزایش مییابد. برعکس، اگر سیستم منبسط شود، کار روی محیط انجام شده (کار منفی است) و انرژی درونی سیستم کاهش مییابد.
همچنین لازم به ذکر است که اگر در گازهای ایدهآل، دما ثابت نگه داشته شود، انرژی درونی سیستم نیز ثابت خواهد بود (). از آنجا که در قانون اول ترمودینامیک بیان شده : (قرارداد آیوپاک) ، نتیجه می شود که : (برای فرآیندهای انبساط یا انقباض همدمای گاز ایدهآل)
نمونه ای از یک فرآیند همدما
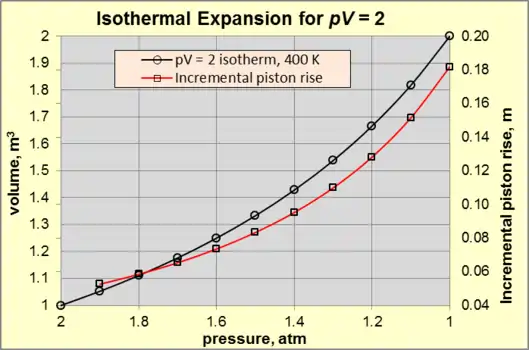
انبساط برگشت پذیر یک گاز ایدهآل را میتوان به عنوان نمونهای از کار انجام شده توسط یک فرآیند همدما نام برد. در این مبحث، حد تبدیل گرما به کار قابل استفاده (مفید) و رابطه بین نیروی محدود کننده و میزان انبساط مورد توجه ویژهای قرار گرفته و بسیار به آن پرداخته میشود.
در حین انبساط همدما ، هر دو کمیت و در امتداد یک ایزوترم (منحنی) قرار گرفتهاند که بر روی آن، عبارت همواره برابر با مقدار ثابتی خواهد بود. یک گاز را در محفظهای استوانهای به ارتفاع 1 متر، مساحت 1 مترمربع و دمای 400 کلوین در تعادل ترمودینامیکی در نظر بگیرید. محیط اطراف از جوی به دمای 300 کلوین و فشار 1 اتمسفر تشکیل شده است. گاز، توسط یک پیستون متصل به بازوی مکانیکی، که نیروی لازم برای ایجاد فشار 2 اتمسفر (حالت A) را اعمال میکند، محدود میشود. بهازای هر تغییری که باعث کاهش نیرو در حالت A شود، گاز منبسط شده و بر محیط اطراف کار انجام میدهد. انبساط همدما، تا زمانی که نیروی وارده کاهش یافته و گرمای درخور اضافه شود، ادامه مییابد تا عبارت را ثابت نگه دارد. اگر حرکت پیستون به اندازه کافی آهسته باشد، انبساط برگشتپذیر است به طوری که در هر لحظه، دما و فشار گاز یکنواخت بوده و در قانون گازهای ایدهآل صدق میکند. شکل 3 رابطه را برای در انبساط همدما از 2 اتمسفر (حالت A) به 1 اتمسفر (حالت B) نشان میدهد.
کار انجام شده ( ) دارای دو مولفه (جزء) میباشد. اولی، کار ناشی از انبساط، در برابر فشار جو اطراف () ؛ و دوم ، کار مکانیکی قابلاستفاده ( ) . در اینجا خروجی میتواند حرکت پیستونی باشد که برای چرخاندن بازوی میل لنگ مورد استفاده قرار میگیرد، که آن هم در ادامه میتواند قرقرهای را که سر دیگر آن به سطل آبی متصل است را چرخانده و سطل را از روی زمین بلند کند.
وقتی نیروی وارد شده به صفر کاهش یابد، سیستم به حالت B () میرسد. در آن نقطه، و خواهند بود. از اختلاف این دو، میتوان نتیجه گرفت که: ؛ که 27.9% از گرمای عرضه شده در فرآیند را تشکیل میدهد. تحت شرایط گفته شده در مثال، این مقدار، حداکثر مقدار کار مکانیکی قابل دستیابی از فرآیند میباشد. درصد تابعی از و فشار جو محیط اطراف است و با نزدیک شدن فشار محیط به صفر اتمسفر، مقدار آن () به 100% نزدیک میشود.
برای آشنایی بیشتر با ماهیت انبساط همدما، به خط قرمز شکل 3 توجه نمایید. مقدار ثابت ، باعث رشد نمایی مقدار صعود پیستون در برابر کاهش فشار میشود. بهعنوان مثال، کاهش فشار از 2 به 1.9 اتمسفر باعث صعود پیستون به اندازه 0.0526 متر میشود. همچنین کاهش فشار از 1.1 به 1 اتمسفر باعث صعود پیستون به میزان 0.1818 متر میشود.
تغییرات آنتروپی
فرآیندهای همدما برای محاسبه تغییرات آنتروپی مناسب میباشند، زیرا در این حالت فرمول تغییر آنتروپی () به سادگی محاسبه میشود :
که در این فرمول، گرمای برگشت یافته به سیستم و دمای مطلق است.[7] این فرمول تنها برای فرآیندهای برگشتپذیر فرضی صادق میباشد؛ یعنی فرآیندی که همواره تعادل در آن برقرار است.
یک مثال ساده، تغییر (گذار) فاز تعادلی (مانند ذوب شدن یا تبخیر) در دما و فشار ثابت میباشد. در تغییر فاز در فشار ثابت، گرمای منتقل شده به سیستم برابر آنتروبی تبدیل ( ) است؛ بنابراین .[3]
هر فشاری، دمای گذار خاص خود ( ) را دارد که در آن، هر دو فاز در تعادل هستند (برای مثال، نقطه جوش طبیعی مایع برای تبخیر در فشار یک اتمسفر). اگر تغییر (گذار) فاز در چنین شرایط تعادلی صورت پذیرد، فرمول فوق را میتوان مستقیما برای محاسبهی تغییرات آنتروپی استفاده کرد:[7]
نمونهای دیگر، میتوان به فرآیند برگشتپذیر انبساط (یا انقباض) همدمای گاز ایدهآل از حجم و فشار اولیهی و تا حجم و فشار نهایی و اشاره نمود. همانطور که در بخش "محاسبه کار" نشان دادهشد، گرمای منتقل شده به گاز برابر است با:
این نتیجه برای فرآیند برگشتپذیر است، بنابراین میتوان آن را در فرمول تغییر آنتروپی جایگزین کرد تا عبارت زیر به دست آید:[7]
از آنجایی که گاز ایدهآل از قانون بویل تبعیت میکند، میتوان این فرمول را به شکل زیر نیز بازنویسی کرد:
این فرمولها را میتوان در یک فرآیند برگشتپذیر، مانند انبساط آزاد گاز ایدهآل، استفاده نمود. چنین انبساطی، همدما نیز میباشد و ممکن است همان شرایط آغازین و نهایی را (همانند انبساط برگشتپذیر) دارا باشد. از آنجا که آنتروپی تابع حالت است، تغییر آنتروپی سیستم مشابه فرآیند برگشتپذیر میباشد؛ و توسط فرمولهای بالا توصیف میشود. توجه داشته باشید که نتیجه () که برای انبساط آزاد گرفته شده بود را نمیتوان در فرمولهای تغییر آنتروپی استفاده نمود؛ چراکه فرآیند برگشتپذیر نیست.
تفاوت میان انبساط آزاد با برگشتپذیر را میتوان در آنتروپی محیط اطراف پیدا کرد. در هر دو حالت، محیطهای اطراف دمای ثابت دارند، پس: . علامت منفی بدین دلیل مورد استفاده قرار میگیرد که گرمای منتقل شده به محیط، از لحاظ مقدار، برابر و از لحاظ علامت، مخالف گرمای انتقال یافته به سیستم () میباشد. در حالت برگشتپذیر، تغییر آنتروپی محیط اطراف، از لحاظ مقدار، برابر و از لحاظ علامت، مخالف تغییرات سیستم میباشد. بنابراین تغییر آنتروپی جهان صفر میباشد. در فرآیند انبساط آزاد، گرما () برابر صفر است؛ بنابراین آنتروپی محیط اطراف تغییری نمیکند و تغییر آنتروپی جهان برابر تغییر آنتروپی () سیستم خواهد بود.
ریشه تاریخی واژه
صفت "همدما (isothermal)" از واژههای یونانی "ἴσος" (معادل "isos") به معنی برابر و "θέρμη" (معادل "therme") به معنی گرما گرفته شدهاست.
جستارهای وابسته
منابع
- Keenan, J. H. (1970). "Chapter 12: Heat-engine cycles". Thermodynamics. Cambridge, Massachusetts: MIT Press.
- Rock, P. A. (1983). "Chapter 11: Thermodynamics of chemical reactions". Chemical Thermodynamics. Mill Valley, CA: University Science Books. ISBN 0-935702-12-1
- Petrucci, R. H.; Harwood, W. S.; Herring, F. G.; Madura, J. D. (2007). "Chapter 12". General Chemistry. Upper Saddle River, NJ: Pearson. ISBN 978-0-13-149330-8
- Klotz, I. M.; Rosenberg, R. M. (1991). "Chapter 6, Application of the first law to gases". Chemical Thermodynamics. Meno Park, CA: Benjamin.
- Adkins, C. J. (1983). Equilibrium Thermodynamics. Cambridge: Cambridge University Press.
- Atkins, Peter (1997). "Chapter 2: The first law: the concepts". Physical Chemistry (6th ed.). New York, NY: W. H. Freeman and Co. ISBN 0-7167-2871-0
- Atkins, Peter (1997). "Chapter 4: The second law: the concepts". Physical Chemistry (6th ed.). New York, NY: W. H. Freeman and Co. ISBN 0-7167-2871-0