معادله لوتکا-ولتررا
معادله لوتکا-ولتررا (به انگلیسی: Lotka–Volterra equation) که همچنین معادلهٔ شکارچی-شکار (به انگلیسی: predator-prey equation) نامیده میشود، یک زوج معادله دیفرانسیلی غیرخطی است که به عنوان مدلی برای سیستمهای زیستی که در آنها دو گونه به صورت شکارچی و شکار وجود دارند، بکار میرود. این معادلات اولین بار توسط آلفرد لوتکا[1] در ۱۹۲۵ و ویتو ولترا[2] ۱۹۲۶ ارائه شدند. این معادلات به صورت زیر بیان میشوند:
که در آنها y تعداد شکارچیها، x تعداد شکارها، t زمان و α، β، γ و δ پارامترهای مشخصه برهمکنش شکارچیها و شکارها است.
- معادله شکارها میشود:
رشد لجستیک شکارها توسط x نشان داده شده که به میزان α در dx تأثیر میگذارد و y نشان دهندهٔ تعداد گونهٔ شکارچی در رشد لجستیک است و به این معناست که به میزان تعداد برخوردهای گونه x و y که برابر است با xy و نرخ شکار شدن β میزان تعداد کم شدن x را نشان میدهد پس به میزان βxy (یا شکار شدن x) از جمعیت لجستیک x در هر وهله تغییراتی زمانی از جمعیت αx کم میکنیم.
- معادله شکارچیها میشود:
در این معادله نشان دهنده افزایش جمعیت شکارچیها است و نشانگر مرگ طبیعی آنهاست (که یک نوع ثابت واپاشی میباشد).
ایزوکلاین نمودار لوتکا ولترا
برای هر معادله دیفرانسیلی میتوان نمودار dot plot کشید اما چنانچه نموداری را در dot plot رسم کنم که در هر نقطه از آن dx/dt صفر شود ایزو کلاین آن نام دارد و از نظر زیستی هر شکلی از آن تحلیل خاصی دارد.
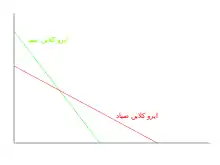
ایزوکلاین صید و صیاد دارای یک نقطه تعادل و پایداری دو گونه
برای هر نقطه در نمودار، تمایل شیب رشدها به سمت نقطه تقاطع دو نمودار است.
ایزوکلاین صید و صیاد دارای سه نقطه تعادل

برای برخی نقاط انقراض صید و برخی صیاد مدنظر است و در نقاطی به تعادل در نقطه تعادل میرسیم.
ایزوکلاین دارای یک نقطه تعادل و انقراض صیاد
برای هر نقطه در نمودار، صیاد منقرض میشود.
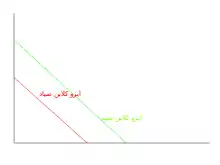
ایزو کلاین دارای یک نقطه تعادل و انقراض صید

برای هر نقطه در نمودار، صید منقرض میشود. (دقت کنید این مدل فقط ریاضیاتی است و تا حد خوبی بر طبیعت منطبق است و نه کاملاً)
منابع
- A.J. Lotka, Elements of physical biology, Williams and Wilkins, Baltimore, Md, USA, 1925.
- V. Volterra, Variazioni e fluttuazioni del numero d'individui in specie animali conviventi, Memorie dell'Accademia Nazionale dei Lincei, Vol. 2 (1926) pp. 31-113.
منابعی برای مطالعه
- Carl I.I. Pistorius, James M. Utterback, A Lotka-Volterra model for multi-mode technological interaction: modeling competition, symbiosis and predator prey modes In: Technology Management in a Changing World, Proceedings of the Fifth International Conference on Management of Technology, Miami, Florida, February 27-March 1, 1996, Pages 3929-96