پدیده‌های کوانتومی ماکروسکوپیک

به‌طور عادی، مکانیک کوانتوم در مقیاس اتمها و ذرات اتمی به کار می‌رود. با این حال، در دماهای پایین، پدیدههایی دیده شده‌است که نشانگر ظهور کوانتوم مکانیک در مقیاس ماکروسکوپیک هستند. شناخته‌شده‌ترین این پدیده‌ها ابرشارگی هلیوم و ابررسانایی هستند که هر دو رفتاری دیدنی به نمایش می‌گذارند. برای نمونه در هر دو حالت ماده می‌تواند با مقاومت صفر جریان یابد. در هلیوم چرخان پیچش‌های کوانتومی شکل می‌گیرند که همه به یک اندازه قوی هستند و می‌توانند در الگوهای زیبایی شکل گیرند.

پدیده‌های کوانتومی ماکروسکوپیک از زیباترین پدیده‌های فیزیک هستند. فصل ۲۱ کتاب درس‌های فاینمن در فیزیک در مورد این مطلب با «این فصل فقط برای سرگرمی است» آغاز می‌شود. در سال‌های ٬۱۹۹۶ ۱۹۹۸ ٬۲۰۰۱، ۲۰۰۳ چهار جایزه نوبل فیزیک به کارهایی در رابطه با این پدیده‌ها داده شد.[1][2][3][4]

پدیده‌هایی که پدیده‌های کوانتومی ماکروسکوپیک خوانده می‌شوند از دو جهت ماکروسکوپیک هستند:

• حالت‌های کوانتومی توسط تعداد زیادی از ذرات اشغال شده‌اند (معمولاً عدد آووگادرو)
• حالت‌های کوانتومی اشغال شده از نظر اندازه ماکروسکوپیک هستند. (اندازه‌ای تا مرتبهٔ کیلومتر در ابررسانا)

نتایج اشغال ماکروسکوپیک حالت‌های کوانتومی

تصویر ۱. چپ: فقط یک ذره؛ حجم کوچک اکثر اوقات خالی است. وسط:تعداد کمی ذره؛ معمولاً جتد ذزه در جعبه هست. راست:تعداد زیادی ذره؛ در این حالت نوسانات حول متوسط ناچیز است.

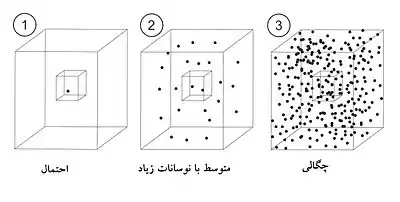
مفهوم اشغال ماکروسکوپیک حالت‌های کوانتومی توسط فریتز لاندن معرفی شد.[5][6]در اینجا توضیح داده خواهد شد که معنای اشغال حالت پایه توسط تعداد بسیاری از ذرات چیست. تابع موج حالت پایه چنین است:

${\displaystyle \Psi =\Psi _{0}\exp(i\varphi )}$

که در آن ${\displaystyle \varphi }$ فاز و ${\displaystyle \Psi _{0}}$ دامنه‌است. تابع موج را نرمال می‌کنیم به طوری که:

${\displaystyle \int \Psi \Psi ^{*}\mathrm {d} V=N_{s}.}$

تعبیر فیزیکی کمیت

${\displaystyle \Psi \Psi ^{*}\Delta V}$

به تعداد ذرات بستگی دارد. تصویر ۱ ظرفی را دارای تعدادی ذره با حجم کنترلی کوچک ΔV در آن نشان می‌دهد. در هر قسمت تعداد ذرات موجود در جعبه کنترلی را حساب می‌کنیم. سه حالت مختلف وجود دارد:

۱. تنها یک ذره وجود دارد. در این حالت حجم کنترلی اکثر اوقات خالی است. هرچند احتمال یافت سدن ذره در این حجم توسط رابطه زیر (همان رابطه قبل) داده می‌شود:

${\displaystyle \Psi \Psi ^{*}\Delta V}$

این احتمال با ΔV متناسب است. عبارت ΨΨ^∗ چگالی احتمال خوانده می‌شود.

۲. اگر تعداد ذره‌ها کمی بیشتر باشد غالباً چند ذر در جعبه یافت می‌شوند. می‌توان یک مقدار متوسط تعریف کرد، اما نوسان تعداد مورد نظر حول این متوسط زیاد است.

۳. در حالت تعداد بسیار زیاد ذره همیشه تعداد زیادی ذره در جعبه کوچک خواهد بود. نوسان تعداد ذرات حول مقدار متوسط کوچک است. مقدار متوسط متناسب با ΔV است و ΨΨ^∗ اکنون به عنوان چگالی ذرات تعبیر می‌شود.

در کوانتوم مکانیک چگالی احتمال شارش ذره J_p (واحد: ذره بر ثانیه بر متر مربع) می‌تواند از معادله شرودینگر به دست می‌آید:

${\displaystyle {\vec {J}}_{p}={\frac {1}{2m}}(\Psi (i{\frac {h}{2\pi }}{\vec {\nabla }}-q{\vec {A}})\Psi ^{*}+cc)}$

که در آن q بار الکتریکی ذره و ${\displaystyle {\vec {A}}}$ پتانسیل برداری است.

${\displaystyle {\vec {J}}_{p}={\frac {\Psi _{0}^{2}}{m}}({\frac {h}{2\pi }}{\vec {\nabla }}\varphi -q{\vec {A}}).}$

اگر تابع موج به‌طور ماکروسکوپیک اشغال شده باشد آنگاه چگالی احتمال شارش ذره تبدیل به احتمال شارش ذره خواهد شد. سرعت شاره v_s را با استفاده از چگالی شارش جرم تعریف می‌کنیم:

${\displaystyle m{\vec {J}}_{p}=\rho _{s}{\vec {v}}_{s}.}$ چگالی (جرم بر متر مکعب) می‌شود:

${\displaystyle m\Psi _{0}^{2}=\rho _{s}}$

بنابراین می‌توان نوشت:

${\displaystyle {\vec {v}}_{s}={\frac {1}{m}}({\frac {h}{2\pi }}{\vec {\nabla }}\varphi -q{\vec {A}}).}$

این رابطهٔ مهم سرعت را که یک مفهوم کلاسیک است را به فاز تابع موج که یک مفهوم کوانتوم مکانیکی است مربوط می‌کند.

چگالش بوز-اینشتین

توزیع سرعت یک گاز از اتم‌های روبیدیوم که ظهور یک حالت جدید ماده٬چگالش بوز-اینشتین را نشان می‌دهد. به ترتیب از چپ به راست: قبل از ظهور چگالش بوز-اینشتین، بلافاصله بعد از آن و مدتی نسبتاً طولانی بعد از آن ٫ که تقریباً چگالش خالص بر جای مانده‌است.

در این قسمت چگالش بوز-اینشتین را بررسی می‌کنیم و دمای T_B را که در دمای کمتر از آن پدیده‌های ماکروسکوپیک کوانتومی روی می‌دهد می‌یابیم. یک سیستم شامل یک مول ذره را در نظر بگیریم تعداد ذرات برابر عدد آووگادرو N_A خواهد بود و حجم آن برابر حجم مولار V_m خواهد بود. چگالی حالت‌ها توسط رابطهٔ زیر داده می‌شود:[7]

${\displaystyle \delta n=D(E)\delta E.}$

(۱)

در اینجا δn تعداد حالات کوانتوم مکانیکی در یک نوار انرژی از E تا E+δE است. برای یک گاز ایدئال با ذراتی به جرم m و اسپین ۰ چگالی حالت‌ها توسط رابطه زیر داده می‌شود:

${\displaystyle D(E)={\frac {2\pi V_{m}(2m)^{3/2}}{h^{3}}}{\sqrt {E}}.}$

(۲)

که در آن h ثابت پلانک است. در آمار بوز-اینشتین در تعداد متوسط ذرات اشغال‌کننده یک حالت کوانتومی برابر است با:

${\displaystyle P(E)={\frac {1}{-1+\exp((E-\mu )/(kT))}}.}$

(۳)

در اینجا μ پتانسیل شیمیایی برای هر ذره و k ثابت بولتزمان است. با استفاده از این معادلات، N_A می‌شود:

${\displaystyle N_{A}={\frac {2\pi V_{m}(2m)^{3/2}}{h^{3}}}\int _{0}^{\infty }{\frac {{\sqrt {E}}\mathrm {d} E}{-1+\exp((E-\mu )/(kT))}}.}$

(۴)

برای اینکه انتگرال در بازه انرژی از ۰ تا ∞ واگرا نشود، باید فرض کنیم:

${\displaystyle \mu <0.}$

(۵)

بنابراین پتانسیل شیمیایی μ می‌تواند برحسب تابعی از T محاسبه شود. در دماهای بالا طبق انتظار μ<۰ خواهد بود. نکته مهم این است که مقدار μ در دمای T_B که بالاتر از صفر است برابر صفر می‌شود. این دما از رابطه‌های قبل با فرض μ=۰ به دست می‌آید. با فرض x=E/kT، به دست می‌آوریم:

${\displaystyle N_{A}=2\pi V_{m}({\frac {2mkT_{B}}{h^{2}}})^{3/2}\int _{0}^{\infty }{\frac {{\sqrt {x}}\mathrm {d} x}{-1+\exp x}}.}$

(۶)

انتگرال توسط روش‌های عددی محاسبه می‌شود. این انتگرال معمولاً بر حسب تابع زتای ریمان نوشته می‌شود:

${\displaystyle \int _{0}^{\infty }{\frac {{\sqrt {x}}\mathrm {d} x}{-1+\exp x}}={\frac {1}{2}}{\sqrt {\pi }}\zeta \left({\frac {3}{2}}\right).}$

(۷)

بنابراین معادله ۶ می‌شود:

${\displaystyle N_{A}=2\pi V_{m}({\frac {2mkT_{B}}{h^{2}}})^{3/2}{\frac {1}{2}}{\sqrt {\pi }}\zeta \left({\frac {3}{2}}\right).}$

(۸)

در نتیجه:

${\displaystyle T_{B}={\frac {h^{2}}{2mk}}({\frac {N_{A}}{2\pi V_{m}{\frac {1}{2}}{\sqrt {\pi }}\zeta ({\frac {3}{2}})}})^{3/2}}$

(۹)

یا:

${\displaystyle T_{B}={\frac {1}{11.918..}}{\frac {h^{2}}{mk}}\left({\frac {N_{A}}{V_{m}}}\right)^{3/2}.}$

(۱۰)

برای مقادیر مربوط به هلیوم مایع (با جرم مولار 0.004 kg/mol و V_m=27.6 cm³/mol) مقدار T_B=3.1 K به دست می‌آید که به مقدار ۲٫۱۷K که نقطه لاندا (T_λ)است و گذار به ابرشارگی در آن دما اتفاق می‌افتد بسیار نزدیک است. با وجود اینکه هلیوم-۴ یک گاز ایدئال نیست این نتایج نشانهٔ این هستند که ابرشارگی ناشی از چگالش بوز-اینشتین است.

یادکردها

1. http://www.nobelprize.org/nobel_prizes/physics/laureates/1996/
2. http://www.nobelprize.org/nobel_prizes/physics/laureates/1998/
3. http://www.nobelprize.org/nobel_prizes/physics/laureates/2001/
4. http://www.nobelprize.org/nobel_prizes/physics/laureates/2003/
5. فریتز لاندن ابرشاره‌ها (لندن، وایلی، ۱۹۵۴–۱۹۶۴)
6. K. Gavroglu and Y. Goudaroulis درک پدیده‌های کوانتومی ماکروسکوپیک: تاریخچه ابرشارگی ۱۹۴۱–۱۹۵۵ Annals of Science, Vol.45, pp. 367-385 (1988)
7. کیتل، آشنایی با فیزیک حالت جامد Physics,وایلی(۱۹۸۶)