تابع زتای ریمان
تابع زتای ریمان یا تابع زتای ریمان-اویلر، ، تابع ریاضیاتی از یک متغیر مختلط چون s است که میتوان آن را به صورت زیر بیان نمود:
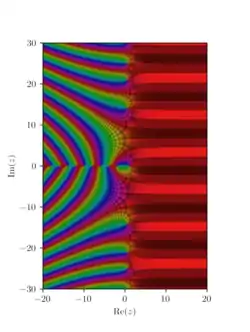
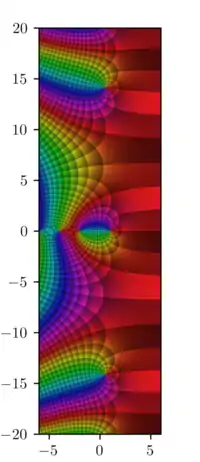
تابع زتای ریمان نقش مهمی در نظریه تحلیلی اعداد داشته و کاربردهایی در فیزیک، نظریه احتمالات، و آمار کاربردی دارد.
لئونارد اویلر اولین بار این تابع را در نیمه اول قرن هجدهم، تنها با استفاده از اعداد حقیقی معرفی و مطالعه نمود، چرا که آنالیز مختلط در آن زمان موجود نبود. مقاله ۱۸۵۹ برنهارت ریمان با عنوان «در مورد تعداد اعداد اول کوچکتر از مقداری داده شده»، تعریف اویلر را به یک متغیر مختلط بسط داده و پیوستگی مرومورفیک و معادله تابعی آن را اثبات نموده و رابطه ای بین صفرهایش و توزیع اعداد اول برقرار نمود.[2]
مقادیر تابع زتای ریمان در اعداد صحیح مثبت زوج، توسط اویلر محاسبه شدند. اولین آنها بود که حلی را برای مسئله بازل ارائه میکند. در ۱۹۷۹، راجر آپری گنگ بودن را اثبات نمود. مقادیر نقاط صحیح منفی نیز که توسط اویلر یافت شدند، اعداد گویا بوده و نقش مهمی را در نظریه فرمهای مدولار (پیمانهای) بازی میکنند. تعمیمهای زیادی از تابع زتای ریمانی چون سریهای دیریکله، L-توابع دیریکله و L-توابع نیز شناخته شده میباشند.
تعریف

تابع زتای ریمان ، تابعی از متغیر مختلط است. (نمادهای s و و t را بهطور سنتی و با پیروی از ریمان، در مطالعه این تابع استفاده میکنند) هنگامی که ، زتای ریمان را میتوان به صورت جمع همگرا یا انتگرال نوشت:
که در آن:
تابع گاما است. تابع زتای ریمان برای سایر مقادیر مختلط، از طریق ادامه تحلیلی در تعریف میگردد.
لئونارد اویلر سری بالا را در ۱۷۴۰ برای مقادیر مثبت صحیح s در نظر گرفت و سپس چبیشف تعریف را برای نیز گسترش داد.[3]
سری فوق نمونه اولیه ای از سری دیریکله است، چنانکه برای sهایی که باشند بهطور مطلق به یک تابع تحلیلی همگرا بوده و برای سایر مقادیر s واگراست. ریمان نشان داد که تابع تعریف شده توسط این سری روی نیم صفحه بالایی را میتوان به تمام مقادیر مختلطی که اند به صورت تحلیلی ادامه داد. برای s=۱، این سری تبدیل به سری هارمونیک شده که به واگرا بوده و:
ازین رو، تابع زتای ریمان روی کل صفحه مختلط s مرومورف است، یعنی تابعی که در همه جا بجز قطب ساده s=۱ هولومورف بوده و در این قطب نیز دارای مانده ۱ میباشد.
فرمول ضرب اویلر
ارتباط این تابع با اعداد اول ابتدا توسط لئونارد اویلر پیدا شد او پی برد:
یک محاسبه نامحدود که همه اعداد اول را در بر میگیرد، نتیجه این محاسبات برای همگراست. این یک نتیجه منطقی از دو نمونه و نتیجه بنیادی در ریاضیات است. این فرمول برای سریهای ژئومتریک و یک قضیه بنیادی علم حساب است.
آقای گائوس ثابت کرد همه اعداد را به صورت نوشت که منظور از همان عدد اول اُم است. اگر بخواهیم مجموعه ای بسازیم تا تمام اعداد طبیعی را بر اساس اعداد اول در خود جای دهد، باید به صورت زیر عمل کنیم:
در عدد m تمامی مقادیر را صفر در نظر می گیریم و برای تمام اعداد حسابی را در نظر می گیریم آنگاه مجموعه زیر تشکیل می شود
حال مجموعه را گسترش می دهیم تا اعداد بیشتری را در اعداد طبیعی محاسبه شود. اینبار را صفر در نظر می گیریم و سپس برای تمام حالات تمام حالات را در نظر می گیریم:
به خوبی مشاهده می شود اعضای مجموعه در توانهای ضرب شده اند تا مجموعه بالا حاصل شود. پس حاصل جمع اعضای مجموعه بالا را می توان به این صورت نوشت
با این ایده، راه حل را گسترش می دهیم و در نهایت پی خواهیم برد مجموع تمام اعداد طبیعی را به صورت زیر می توان نوشت
در معکوس اعداد طبیعی نیز با همین ایده پیش می رویم و ضرب اویلر می رسیم
تساوی دیگری که می توان به آن دست یافت به صورت زیر است:
مقادیر خاص
در پایین بیشترین استفاده از مقادیر تابع زتاریمان که عمومیت دارند نشان داده میشود.
- ; بازل.
صفرهای تابع زتای ریمان
تابع زتاریمان در اعداد صحیح منفی صفر دارد (به معادلهٔ تابع توجه کنید) به این صفرها، صفرهای بدیهی گویند آنها فقط جزئی اند به این خاطر اثبات وجود آنها آسان است. برای مثال از رابطه گاما که در پایین امده است. صفرهای غیر بدیهی که در نظر گرفته میشود بیشتر با توجه به دلیل اینکه توزیع آنها نه تنها کم قابل درک است حتی مهمتر از آن اینست که به صورت حیرت آوری رگهای در پرسشهای ریاضی باز میکند. می دانیم که هر صفر غیر بدیهی تابع زتاریمان در نوار باز {s ∈ C: 0 <Re(s) <1}، که نوار بحرانی نام دارد. فرضیه ریمان اظهار میدارد که هر صفر غیر بدیهی دارای Re(s) = 1/2 است. در قضیه تابع زتاریمان، {s ∈ C: Re(s) = 1/2} خط بحرانی نامیده میشود. جایگاه صفرهای تابع زتاریمان، اهمیت بسیاری در نظریه اعداد دارد. از حقیقت اینکه تمام صفرهای غیر بدیهی در نوار بحرانی قرار دارند، یک میتوان نظریه اعداد اول را استنتاج کرد. و یک نتیجه بهتر اینست که:
قویترین نتیجه از این بحث اینست که را میتوان درستی نظریه ریمان را انتظار داشت که نتایج بسیار ژرفی در نظریه اعداد دارد. این معلوم است که تعداد نامتناهی نوار بحرانی وجود دارد. لیتلوود نشان داد که اگر دنباله (γn) قسمت موهومی و همه صفرهای صفحه بالایی را شامل میشود که:
قضیه نوار بحرانی ادعا میکند که درصد مثبتی از صفرهای غیر بدیهی در نوار بحرانی قرار دارد. در نوار بحرانی، صفر با کوچکترین قسمت موهومی غیر منفی 1/2+i14.13472514... مستقیماً از معادلهٔ تابعی دیده میشود که صفر غیر بدیهی متقارن اند حول Re(s) = 1/2 اگر چه ζ(s)=ζ(s*)* برای تمام اعداد مختلط s ≠ 1 بکار میرود که صفرهای تابع زتاریمان حول قسمت حقیقی متقارن و موجودند. گادفری هرلد هاردی اثبات کرد تباع زتای ریمان بینهایت صفر دارد.(هاورد و. ایوز، صفحهٔ ۲۵۸)- امروزه اثبات فرضیه ریمان که به RH معروف است مهمترین مسئله اثبات نشده ریاضی است و برای اولین اثبات صحیح یک میلیون دلار جایزه تعیین شدهاست .
معادله تابعی
تابع زتا، معادلهٔ تابعی زیر را مشخص میکند:
که برای تمام sهای در C\{0,1}. معتبر است (صدق میکند)، در اینجا منظور از Γ همان تابع گاماست این فرمول برای ساختن آنالیز پیوسته بکار میرود. در S = 1، تابع زتا مانند مانده در قطب 1 است.معادله همچنین نشان میدهد که تابع زتا، صفر بدیهی از -2 , -4 , … دارد. همچنین وجود دارد نمونهای متقارن از معادلهٔ تابع که در همان تعریف اولیه را میدهد
این معادله بهوسیلهٔ این معادله بدست آمدهاست:
خواص مختلف
معکوس
معکوس تابع زتا از سری دریکله روی معادلهٔ موبیوس نتیجه میشود.
برای هر عدد مختلط s با .، وجود دارد عددی، از رابطه مشابه که مستلزم اعداد متفاوت است که مشخص میکند تابع ضربی را که محاسبات ریاضیات را روی سری دریکله میدهد. در بالا و با بیان تعارف برای ζ(2)، میتوان برای حل امتحان دو پیشامد که عدد صحیح را میدهد استفاده کرد که برابر 6/π2 است. فرض ریمان هم ارز است با این ادعا که اظهار میکند که وجود دارد وقتی که . است.
نمایشها
انتگرالهای نوع ملین
تبدیل ملین از یک تابع fe (x) به صورت زیر تعریف میشود.
در ناحیهای که انتگرال تعریف میشود، تعبیرهای متفاوتی برای تابع زتا در تبدیل ملین وجود دارد. اگر قسمت حقیقی S بزرگتر از 1 باشد داریم:
با حذف جمله اول بسط سری توانی از 1/(exp(x)& حول صفر، ما میتوانیم در دیگر نواحی نیز تابع زتا را بدست آوریم با جزئیات در نوار بحرانی خواهیم داشت:
و وقتی قسمت حقیقی بین 0 , -1 باشد داریم:
و ما میتوانیم همچنین پیدا کنیم جملاتی را که با اعداد اول رابطه دارند. اگر π(x) یک تابع محاسبه اعداد اول باشد پس
برای مقادیری با . میتوانیم رابطهای بالا را با تبدیل ملین از π(x) by پیدا کنیم.
که
یک مشابه تبدیل ملین مستلزم اینست که تابع J(x) محاسبهای اعداد اول ریمان که اعداد ( pn ) اول توانی را محاسبه میکند با وزن 1/nپس . حال داریم:
فرمول این تعبیر میتواند برا حل تئوری اعداد اول استفاده شود. بهوسیلهٔ معکوس تبدیل ملین کار کردن با تابع محاسبه اعداد اول ریمان آسانتر است و میتواند با استفاده از آن بهوسیله معکوس موبیوس بهبود یابد.
جستارهای وابسته
منابع
- "Jupyter Notebook Viewer". Nbviewer.ipython.org. Retrieved 2017-01-04.
- This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is considered by many mathematicians to be the most important unsolved problem in pure mathematics. Bombieri, Enrico. "The Riemann Hypothesis – official problem description" (PDF). Clay Mathematics Institute. Retrieved 2014-08-08.
- Devlin, Keith (2002). The Millennium Problems: The seven greatest unsolved mathematical puzzles of our time. New York: Barnes & Noble. pp. 43–47. ISBN 978-0-7607-8659-8.
- مشارکتکنندگان ویکیپدیا. «Riemann Zeta Function». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۱ آوریل ۲۰۲۱.
