مکعب (جبر)
[[پرونده:X cubed plot.svg|بندانگشتی|}} نمودار {{math|y = x3 در مختصات کارتزین]] در حساب و جبر، مکعب یا توان سوم نتیجه سه بار ضرب یک عدد در خودش است.
همچنین مکعب حاصل ضرب مربع یک عدد در خودش است.
توان سوم، حجم یک مکعب با وجوه برابر را بدست میآورد. تابع وارون برای یافتن عددی که مکعب آن برابر با n است، ریشه سوم عدد n است. توان سوم و ریشه سوم هر دو توابعی فرد هستند.
مکعب هر عدد یا عبارت ریاضی به وسیلهٔ بالانویس نمایش داده میشود، مانند:
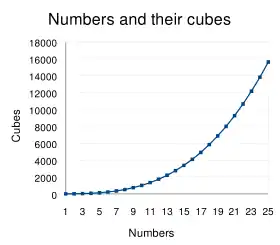
نمودار تابع y = x3 یک سهمی است. چون مکعب تابعی فرد است این سهمی دارای یک نقطه تقارن در مبدأ ولی فاقد تقارن چرخشی است.
اعداد صحیح
مکعب کامل عددی صحیح و مکعب یک عدد صحیح است. مکعبهای کامل تا ۶۰۳ براساس دانشنامه برخط دنبالههای صحیح به شرح زیر است:
| ۰۳ = | ۰ | ||||||||||
| ۱۳ = | ۱ | ۱۱۳ = | ۱۳۳۱ | ۲۱۳ = | ۹۲۶۱ | ۳۱۳ = | ۲۹٬۷۹۱ | ۴۱۳ = | ۶۸٬۹۲۱ | ۵۱۳ = | ۱۳۲٬۶۵۱ |
| ۲۳ = | ۸ | ۱۲۳ = | ۱۷۲۸ | ۲۲۳ = | ۱۰٬۶۴۸ | ۳۲۳ = | ۳۲٬۷۶۸ | ۴۲۳ = | ۷۴٬۰۸۸ | ۵۲۳ = | ۱۴۰٬۶۰۸ |
| ۳۳ = | ۲۷ | ۱۳۳ = | ۲۱۹۷ | ۲۳۳ = | ۱۲٬۱۶۷ | ۳۳۳ = | ۳۵٬۹۳۷ | ۴۳۳ = | ۷۹٬۵۰۷ | ۵۳۳ = | ۱۴۸٬۸۷۷ |
| ۴۳ = | ۶۴ | ۱۴۳ = | ۲۷۴۴ | ۲۴۳ = | ۱۳٬۸۲۴ | ۳۴۳ = | ۳۹٬۳۰۴ | ۴۴۳ = | ۸۵٬۱۸۴ | ۵۴۳ = | ۱۵۷٬۴۶۴ |
| ۵۳ = | ۱۲۵ | ۱۵۳ = | ۳۳۷۵ | ۲۵۳ = | ۱۵٬۶۲۵ | ۳۵۳ = | ۴۲٬۸۷۵ | ۴۵۳ = | ۹۱٬۱۲۵ | ۵۵۳ = | ۱۶۶٬۳۷۵ |
| ۶۳ = | ۲۱۶ | ۱۶۳ = | ۴۰۹۶ | ۲۶۳ = | ۱۷٬۵۷۶ | ۳۶۳ = | ۴۶٬۶۵۶ | ۴۶۳ = | ۹۷٬۳۳۶ | ۵۶۳ = | ۱۷۵٬۶۱۶ |
| ۷۳ = | ۳۴۳ | ۱۷۳ = | ۴۹۱۳ | ۲۷۳ = | ۱۹٬۶۸۳ | ۳۷۳ = | ۵۰٬۶۵۳ | ۴۷۳ = | ۱۰۳٬۸۲۳ | ۵۷۳ = | ۱۸۵٬۱۹۳ |
| ۸۳ = | ۵۱۲ | ۱۸۳ = | ۵۸۳۲ | ۲۸۳ = | ۲۱٬۹۵۲ | ۳۸۳ = | ۵۴٬۸۷۲ | ۴۸۳ = | ۱۱۰٬۵۹۲ | ۵۸۳ = | ۱۹۵٬۱۱۲ |
| ۹۳ = | ۷۲۹ | ۱۹۳ = | ۶۸۵۹ | ۲۹۳ = | ۲۴٬۳۸۹ | ۳۹۳ = | ۵۹٬۳۱۹ | ۴۹۳ = | ۱۱۷٬۶۴۹ | ۵۹۳ = | ۲۰۵٬۳۷۹ |
| ۱۰۳ = | ۱۰۰۰ | ۲۰۳ = | ۸۰۰۰ | ۳۰۳ = | ۲۷٬۰۰۰ | ۴۰۳ = | ۶۴٬۰۰۰ | ۵۰۳ = | ۱۲۵٬۰۰۰ | ۶۰۳ = | ۲۱۶٬۰۰۰ |
از نظر هندسی عدد صحیح مثبت m یک مکعب کامل است اگر و تنها اگر بتوان m تعداد مکعب واحد را طوری منظم کرد که یک مکعب کامل بزرگتر را ایجاد کنند. برای مثال چون ۲۷=۳×۳×۳ است، میتوان با ۲۷ مکعب واحد یک مکعب روبیک ساخت.
اختلاف میان مکعب اعداد صحیح متوالی را میتوان به صورت زیر بیان کرد:
n3 − (n − 1)3 = 3(n − 1)n + 1
یا
(n + 1)3 − n3 = 3(n + 1)n + 1
نمیتوان حداقلی برای مکعب کامل تعریف کرد زیرا مکعب اعداد صحیح منفی نیز عددی منفی است، مانند: ۶۴-=۴-×۴-×۴-
جستارهای وابسته
منابع
- مشارکتکنندگان ویکیپدیا. «Cube (algebra)». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۹ اکتبر ۲۰۱۷.
