رویه ریمانی

رویه‌های ریمانی به‌طور عام، مجموعه اشیایی در ریاضی است که در آن‌ها امکان تعریف و توسعه توابع مختلط (تحلیلی یا دارای تَکینی) و هارمونیک شدنی است. به سخن ساده‌تر، همانند فضاهای برداری که محلی برای تعریف و توسعه توابع و نگاشت‌های خطی اند، رویه‌های ریمانی نیز محلی برای تعریف و توسعه آنالیز و توابع مختلط می‌باشند.

برشی از یک سطح ریمانی که از به هم چسباندن دو صفحه مختلط به دست آمده‌است. این سطح برای تعریف ${\displaystyle {\sqrt {z}}}$ وقتی که ${\displaystyle z}$ یک متغیر مختلط است به کار می‌رود.

تعریف و تعاریف معادل

برای تعریف یک سطح ریمانی، یا سطوح ریمانی، راه‌های متفاوت و طبیعتاً معادلی وجود دارند. یکی از ساده‌ترین و در عین حال شهودی‌ترین شیوه تعریف یک سطح ریمانی به اینگونه است: یک سطح ریمانی یک منیفولد (چند تایی/خمینه) مختلط (Complex Manifold) از بعد یک است.

به بیان دقیق تر، یک سطح ریمانی، یک فضای توپولوژیک هاسدورف، جدایی پذیر و همبند است که موضعاً شبیه زیرمجموعه‌های باز، همبند و سَره (محض) در صفحه مختلط می‌باشد. بخش آخر تعریف به معنای این است که برای هر نقطه از فضا یک همسایگی وجود دارد که با یک زیرمجموعه‌های باز، همبند و سَره (محض) در صفحه مختلط همسان توپولوژیک یا همان همسان‌ریخت است.

شیوه دیگر تعریف یک سطح ریمانی این است: یک سطح ریمانی یک منیفولد دیفرانسیل پذیر حقیقی از بعد دو به همراه یک اطلس (خانواده ماکسیمال از کارت‌ها) است به گونه‌ای که هر عضو اطلس یک هومیومرفیسم بین یک زیرمجموعه باز از منیفولد و یک گوی باز در صفحه مختلط بوده و نگاشت‌های انتقالی بین دو عضو اطلس با اشتراک ناتهی یک تابع تحلیلی مختلط باشند.

با نمادهای ریاضی، اگر ${\displaystyle (M,\Phi )}$ نمایش یک سطح ریمانی باشد،${\displaystyle M}$ نشان دهنده فضای توپولوژیک زمینه و ${\displaystyle \Phi =\{(\phi _{k},u_{k})\}_{k}}$ نشان دهنده اطلس با ویژگی ذکر شده‌است: هر ${\displaystyle \phi _{k}:u_{k}\subset M\rightarrow v_{k}\subset \mathbb {C} }$ یک همیومرفیسم است و اگر${\displaystyle u_{i}\cap u_{j}\neq \emptyset }$ آنگاه${\displaystyle \phi _{i}\circ \phi _{j}^{-1}:\phi _{j}(u_{i}\cap u_{j})\rightarrow \phi _{i}(u_{i}\cap u_{j})}$ یک تابع هولومرفیک (بین دو زیر مجموعه از صفحه مختلط) است. برای راحتی، به مجموعه کارت‌ها یا همان اطلس ${\displaystyle \Phi }$ یک ساختار مختلط بر ${\displaystyle M}$ می‌گویند.

کاملاً طبیعی است که بر یک فضای توپولوژیک ثابت زمینه، بتوان چندین ساختار مختلط متفاوت تعریف کرد. بررسی رابطه بین این ساختارها و چگونگی تبدیل آن‌ها به یکدیگر، به تنهایی شاخهٔ عمیق دیگری از ریاضیات نوین (قرن بیستم) می‌باشد که به‌طور عام نظریه تایکمولِر نامیده می‌شود.

اگرچه این سطوح موضعا، ساده به نظر می‌رسند ولی در نگاه کلی می‌توانند به لحاظ جبری (گروه اصلی، گروه‌های کوهومولوژی)، توپولوژیکی (تعداد دسته ها(genus) یا همان گونه، دگردیسی‌ها)، هندسی (خمیدگی یا همان انحنا، مساحت کل، فرم‌ها) و تحلیلی (تعریف توابع تحلیلی یا دارای تکینی بر یا بین آنها، تعمیم مشتق و انتگرال) بسیار بسیار پیچیده باشند و در واقع اینگونه هستند.

سطوح ریمانی به مجموعه اشیا هندسی با خواص ذکر شده، گفته می‌شود. همان‌طور که گفته شد این سطوح حالت خاصی از منیفولدهای مختلط می‌باشند بنابراین طبیعی است که این سطوح نه فقط دارای کاربردهای وسیعی در ریاضی که در فیزیک (به عنوان مثال نظریه ریسمان) نیز بسیار پرکاربرد می‌باشند.

تاریخچه

این سطوح برای اولین بار، به‌طور مدون، در رساله دکترای ریاضی‌دان بزرگ آلمانی برنهارت ریمان، در سال ۱۸۵۱ کشف/ابداع و سپس توسط خود ریمان و بسیاری دیگر از ریاضی دانان قرن بیستم گسترش و تعمیم پیدا کرد. اگرچه ایده اولیه آن به سالهای قبل تری برمی گردد (به ویژه کارهای عمیق ریاضی دانانی چون کوشی، آبِل، گائوس، یاکوبی) ولی ریمان اولین فردی بود که آن‌ها را به‌طور حرفه‌ای تعریف و به کار برد. ریمان متوجه این مطلب شده بود که توابعی مانند ${\displaystyle {\sqrt {z}}}$ یا ${\displaystyle \log z}$، زمانی که ${\displaystyle z}$ یک متغیر مختلط است، بر صفحه مختلط خوش تعریف نمی‌باشند و برای تعریف آن‌ها به صورت تابعی خوش تعریف نیاز به گسترش صفحه مختلط، به حالت عام تری است.

طرح گونه‌ای از سطح ریمانی که برای تعریف تابع لگاریتم ${\displaystyle \log z}$ با متغیر مختلط به کار می‌رود. هر طبقه در واقع یک صفحه مختلط کامل است و این شکل تنها بخش کوچکی از این سطح را نمایش می‌دهد.

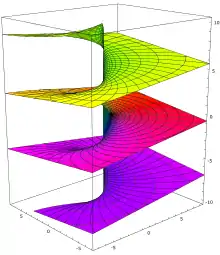
مثال‌هایی مقدماتی از سطوح ریمانی

صفحه مختلط، هر زیر مجموعه باز (نه الزاماً همبند) از صفحه مختلط مانند دیسک (گوی باز) یا دیسک محذوف (گوی باز بدون مرکز)، کره ریمان، تویوپ (چمبره یا تورس) با ساختار مختلط (البته کمی نیاز به توضیح دارد).

دیگر مثال‌ها را می‌توان با چسباندن چند (متناهی یا نا متناهی) صفحه مختلط به یکدیگر به دست آورد. مانند صفحه‌ای که برای تعریف توابع ${\displaystyle {\sqrt {z}}}$ یا ${\displaystyle \log z}$ به کار می‌روند. به تصویرها مراجعه شود.

طرح گونه‌ای از یک سطح ریمانی فشرده با دو دسته.

دسته‌بندی

دسته‌بندی‌های گوناگونی از این سطوح وجود دارد. به برخی از آن‌ها در ادامه اشاره می‌کنیم.

• یکی از آن‌ها که بیشتر توپولوژیک می‌باشد این است که در حالت کلی می‌توان آن‌ها را به دو دسته فشرده و غیر فشرده تقسیم کرد.
• دیگر دسته‌بندی این سطوح که بیشتر بر مبنای پوشش جامع (Universal Cover) می‌باشد، به این شرح است: سطوح بیضوی، سطوح هذلولوی، سطوح سهموی.

برای مطالعه سطوح ریمانی حداقل دو شیوه یا روش را می‌توان در پیش گرفت، یکی از راه مطالعه هندسه جبری و مطالعه هندسی توابع جبری می‌باشد که بیشتر متمرکز بر مطالعه سطوح فشرده‌است و شیوه دیگر، بررسی و مطالعه آن‌ها از مسیر مطالعه آنالیز مختلط یا همان نظریه توابع مختلط می‌باشد. در شیوه دوم، که بیشتر تحلیلی نامیده می‌شود، سطوح نافشرده نیز به‌طور گسترده بررسی می‌شوند.

توابع بر سطوح ریمانی

به‌طور کلی توابع خوش رفتار با برد مختلط بر این سطوح را می‌توان به دو دسته تقسیم کرد: توابع تحلیلی یا همان هولومرف و توابع دارای تکینی یا همان مرومورف. لازم است ذکر شود که مانند صفحه مختلط، بر این سطوح توابع ِ هارمُنیک با برد حقیقی نیز تعریف شده و دارای کاربردهای وسیعی می‌باشد.

سطوح ریمانی و هندسه ریمانی

در ترجمه به زبان فارسی، توجه شود که سطوح ریمانی ترجمه Riemann Surfaces است و با Riemannian Geometry که هندسه ریمانی می‌باشد تفاوت زیاد و بنیادینی دارد. به‌طور خاص، به معنای ریاضی چیزی به نام Riemannian Surfaces تا به الان وجود نداشته و بی‌معنی است.

لازم است ذکر شود که همواره می‌توان بر یک سطح ریمانی (اگر آنرا فقط یک منیفلد ببینیم) یک هندسه ریمانی قرار داد، به بیان دقیقتر یک متریک ریمانی کامل با انحنا ثابت، ولی در آنالیز مختلط توجه و تمرکز، بیشتر بر بررسی ساختار مختلط این سطوح است.

همچنین تفاوت یک سطح ریمانی با فضای توپولوژیک زمینه اش را نمی‌توان به‌طور شهودی تشخیص داد! به‌طور مثال نمی‌توان با نگاه کردن به دو کره گفت که کدام یک، یک سطح ریمانی و کدام یک صرفاً یک کره (به عنوان یک فضای توپولوژیک) است. یک سطح ریمانی به‌طور مشترک با ساختار توپولوژیک آن و ساختار مختلط آن (اطلس‌ها یا همان کارت‌ها به صفحه مختلط) شناخته می‌شود. به همین علت در تصاویر و شکل‌ها فقط می‌توان طرح گونه‌ای از آن را برای تصور بهتر به تصویر کشید.

قضایا و روابط مهم

سطوح ریمانی مانند هر بخش دیگری از ریاضی دارای قضایای مهم خاص خود می‌باشد. در اینجا، به منظور روشن‌تر شدن محتوا، به برخی از مهم‌ترین و در عین حال مقدماتی‌ترین آن‌ها اشاره‌ای می‌شود.

• تنها تابع هولومرفیک (تحلیلی) بر یک سطح ریمانی فشرده، تابع ثابت است.
• هر تابع مرومورفیک بر کره ریمانی یک تابع گویا است، به بیان دیگر می‌توان آنرا به صورت تقسیم دو چند جمله‌ای (با ضرایب مختلط) نوشت.
• فرض کنید که ${\displaystyle f:M\rightarrow N}$ یک تابع هولومرفیک بین دو سطح ریمانی باشد، در هر نقطه ${\displaystyle z\in M}$ همواره می‌توان یک کارت${\displaystyle (U_{1},\phi _{1})}$ از ${\displaystyle M}$ حول ${\displaystyle z}$ و یک کارت ${\displaystyle (U_{2},\phi _{2})}$از ${\displaystyle N}$ حول ${\displaystyle f(z)}$ چنان پیدا کرد که ${\displaystyle \phi _{2}(f({\phi _{1}}^{-1}(w))=w^{n}}$ به ازای هر ${\displaystyle w\in \phi _{1}(U_{1})}$. به بیان ساده‌تر توابع هولومرفیک، موضعا مانند چندجمله ای‌ها رفتار می‌کنند.
• فرض کنید که ${\displaystyle z\in M}$ یک سطح ریمانی فشرده باشد، بر این سطح همواره یک تابع مرمورفیک وجود دارد. این قضیه علی‌رغم ظاهری ساده دارای اثباتی نسبتاً دشوار و عمیق است، هم چنین به کمک آن نتایج بسیاری را در نظریه سطوح ریمانی می‌توان به دست آورد. به عنوان مثال به کمک آن می‌توان اثبات کرد که هر سطح ریمانی فشرده‌ای را می‌توان مثلث بندی کرد.
• فرض کنیم که دو تابع هولومرفیک بر یک زیر مجموعه باز و سره ${\displaystyle U}$ از یک سطح ریمانی تعریف شده و بر یک زیر مجوعه دارای نقطه انباشتگی از آن با هم برابر باشند، در این صورت این دو تابع بر کل ${\displaystyle U}$ با هم برابراند.
• قضیه ریمان-راک: این قضیه (به بیان ساده) در مورد بُعد فُرم‌های مرمورفیک بر یک سطح ریمانی فشرده‌است.
• قضیه ریمان-هِرویتز: این قضیه رابطه‌ای عددی بین تعداد دسته ها(genus)ی سطوح‌های ریمانی ${\displaystyle M}$و ${\displaystyle N}$و درجه یک تابع هولومرفیک ${\displaystyle f:M\rightarrow N}$بین آن دو را بیان می‌کند.
• سطوح ریمانی فشرده با دو دسته (genus) یا بیش دارای انحنای منفی، با یک دسته (چمبره) دارای انحنا صفر و بدون دسته (کره ریمانی) دارای انحنای مثبت‌اند. این ویژگی صرفاً یک ویژگی توپولوژیکی (مستقل از هندسه و ساختار مختلط) این سطوح است.
• امکان تعریف یک ساختار مختلط بر بطری کلاین و نوار موبیوس وجود ندارد. دلیل این امر جهت ناپذیری (non-orientable) این سطوح است.

جستارهای وابسته

• صفحه مختلط
• تابع تحلیلی مختلط
• تابع هارمونیک
• هندسه ریمانی
• اعداد مختلط
• هندسه ریمانی
• قضیه ریمان-راک
• قضیه ریمان-هِرویتز

منابع

• Lectures on Riemann Surfaces, Otto Forster, Springer-Verlag, 1999.
• Riemann Surfaces, Lars Valerian Ahlfors & Leo Sario, Harvard university press, 1960.

پیوند به بیرون

• "Riemann surface", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Riemann Surface at PlanetMath.