استدلال قطری کانتور

در نظریه مجموعه‌ها، استدلال قطری کانتور در سال ۱۸۹۱ توسط گئورگ کانتور به عنوان یک اثبات ریاضی ارائه گردید و نشان داد مجموعه‌های بی‌نهایتی وجود دارند که اعضای آن‌ها در تناظر یک به یک با محموعه اعداد طبیعی نیستند.[1][2][3] چنین مجموعه‌هایی را «مجموعه ناشمارا» می‌نامند.

یک تصویر از استدلال قطری کانتور (در مبنای ۲) برای اثبات وجود مجموعه‌های غیرقابل شمارش. دنباله پایین (s) نمی‌تواند در هیچ‌یک از توالی‌های بالا رخ دهد.
یک مجموعه نامتناهی ممکن است دارای همان کاردینالیتی باشد که زیر مجموعه مناسب آن دارد. مثلاً مجموعه اعداد طبیعی با مجموعه اعداد زوج می تواند تناظر یک به یک برقرا نماید. با این وجود بی‌نهایت‌هایی با کاردینالیتی‌های متفاوت وجود دارند که استدلال قطری کانتور وجود آن‌ها را اثبات می‌نماید.

مجموعه غیرقابل شمارش

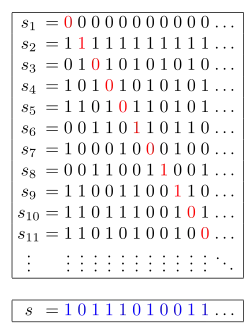
کانتور، در مقاله‌ی خود در سال ۱۸۹۱، مجموعه T‌ را مطالعه کرد که شامل همه دنباله‌های رقم‌های دودویی (یعنی هر رقم صفر یا یک) باشد. او با اثباتی ساختی از قضیه زیر شروع می‌کند:

اگر s1, s2, … , sn شامل تمامی شمارش‌های ممکن از T باشد، آنگاه همواره عضوی از T وجود خواهد داشت که در بین s1,S2,... نخواهد بود.

برای اثبات این، محموعه‌هایی از T را به شکل زیر انتخاب می‌نماییم:

s1 = (۰, ۰, ۰, ۰, ۰, ۰, ۰, ...)
s2 = (۱, ۱, ۱, ۱, ۱, ۱, ۱, ...)
s3 = (۰, ۱, ۰, ۱, ۰, ۱, ۰, ...)
s4 = (۱, ۰, ۱, ۰, ۱, ۰, ۱, ...)
s5 = (۱, ۱, ۰, ۱, ۰, ۱, ۱, ...)
s6 = (۰, ۰, ۱, ۱, ۰, ۱, ۱, ...)
s7 = (۱, ۰, ۰, ۰, ۱, ۰, ۰, ...)
...

او ساختار توالی s را با انتخاب مکمل اولین رقم در s1 انتخاب نمود (جایگزینی صفر به جای یک و برعکس)، برای انتخاب دومین رقم S به سراع رقم دوم در s2 رفت و مکمل آن را انتخاب نمد و به همین ترتیب ادامه داد. در مثال فوق به نتایج زیر می‌رسیم:

s1 = (۰, ۰, ۰, ۰, ۰, ۰, ۰, ...)
s2 = (۱, ۱, ۱, ۱, ۱, ۱, ۱, ...)
s3 = (۰, ۱, ۰, ۱, ۰, ۱, ۰, ...)
s4 = (۱, ۰, ۱, ۰, ۱, ۰, ۱, ...)
s5 = (۱, ۱, ۰, ۱, ۰, ۱, ۱, ...)
s6 = (۰, ۰, ۱, ۱, ۰, ۱, ۱, ...)
s7 = (۱, ۰, ۰, ۰, ۱, ۰, ۰, ...)
...
s = (۱, ۰, ۱, ۱, ۱, ۰, ۱, ...)

با ساخت s به روش فوق به مجموعه‌ای می‌رسیم که با تمامی مجمه‌های بالا متفاوت است زیرا عنصر n ام آن با عنصر n ام تمام مجموعه‌های بالا تفاوت دارد.

بر اساس این قضیه کانتور با استفاده از یک اثبات با تناقض نشان می‌دهد که:

مجموعه T غیرقابل شمارش است.

او برای اثبات تناقض در ابتدا فرض می‌کند T شمارا است. پس همه عناصر آن به شکل s1,s2,...sn قابل نمایش هستند. با اعمال قضیه قبلی به این شمارشها به توالی s می‌رسیم که در شمارش‌ها موجود نیست. اما s عنصری از T بود و بنابراین باید در شمارش‌ها باشد. این تضاد فرض اصلی را زیر سؤال می‌برد بنابراین T غیرقابل شمارش است.

منابع
  1. Georg Cantor (1891). "Ueber eine elementare Frage der Mannigfaltigkeitslehre". Jahresbericht der Deutschen Mathematiker-Vereinigung 1890–1891. 1: 75–78 (84–87 in pdf file).
  2. Keith Simmons (30 July 1993). Universality and the Liar: An Essay on Truth and the Diagonal Argument. Cambridge University Press. pp. 20–. ISBN 978-0-521-43069-2.
  3. Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). New York: McGraw-Hill. p. 30. ISBN 0-07-085613-3.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.