تعادل نش زیربازی کامل

در نظریه ی بازی ها (به انگلیسی:Game theory)، تعادل نش زیربازی کامل(SPNE) یکی از روش‌های یافتن تعادل نش(Nash Equilibrium) است که در بازی‌های حرکتی(dynamic games) مورد استفاده قرار می‌گیرد. مشخصات استراتژی های (S* (strategy profiles در یک بازی به شکل گسترده، که از یافتن تعادل نش تمام زیربازی‌های کل بازی بدست می‌آید، یک تعادل نش زیربازی کامل است.[1]

تعریف زیربازی (subgame)

یک زیربازی از یک بازی به فرم گسترده با اطلاعات کامل، یک زیرمجموعه از بازی است اگر دو مشخصه زیر را داشته باشد:

1. با یک گره‌ای (node) که پایانی نیست، آغاز شود.
2. تمامی گره‌هایی را که در ادامه این گره قرار دارند، شامل شود؛ و تنها همین دسته از گره‌ها را شامل شود.

تعریف استقرای معکوس (Backward Induction)

یک روش معمول برای یافتن تعادل نش زیربازی کامل در بازی‌های متناهی، استفاده از استقرای معکوس (backward induction) می‌باشد. سؤالی که در این جا ممکن است مطرح شود این است که چرا در بازی‌های پویا نمی‌توان با نوشتن فرم استراتژیک (strategic form) بازی، تعادل را یافت؟ برای پاسخ به این سؤال، به بازی زیر که به بازی ورود به یک صنعت (An Entry Game) معروف است، توجه کنید(به "شکل گسترده بازی ورود به یک صنعت" توجه شود.):

شکل گسترده ی بازی ورود به یک صنعت

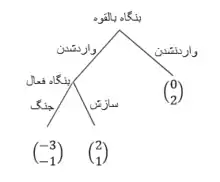
فرم استراتژیک این بازی بدین شکل است (به شکل "فرم استراتژیک بازی" توجه شود):

فرم استراتژیک بازی

بدون درنظرگرفتن ساختار ترتیبی این بازی، دو تعادل نش خواهیم یافت:

(سازش اگر بنگاه بالقوه وارد بازار شود و واردشدن)

(جنگ اگر بنگاه بالقوه وارد بازار شود و واردنشدن)

اما تعادل نش دوم، عقلانی به نظر نمی‌رسد. چون بنگاه بالقوه درک می‌کند که اگر استراتژی "واردشدن" را اتخاذ کند، برای بنگاه فعال بهینه این است که به جای استراتژی "جنگ"، استراتژی "سازش" را انتخاب کند؛ چرا که با انتخاب استراتژی "جنگ"، دریافتی بنگاه فعال 1- می‌شود ولی با بازی کردن استراتژی "سازش"، دریافتی وی برابر با 1 خواهد بود. درحقیقت، اتخاذ استراتژی جنگ توسط بنگاه فعال، یک تهدید معتبر نمی‌باشد. این مشکل به دلیل در نظر نگرفتن طبیعت ترتیبی این بازی به وقوع می پیوندد. بنابراین به دلیل بروز این مشکل به نظر می‌رسد برای یافتن تعادل در بازی‌های پویای متناهی، نیاز به یک مفهوم قوی تر نسبت به تعادل نش داریم. این مفهوم قوی تر، "استقرای معکوس" می‌باشد.

استقرای معکوس برای به تحقق رساندن ایدهٔ عقلانیت ترتیبی (sequential rationality) در بازی‌های متناهی با اطلاعات کامل (finite games of perfect information) استفاده می‌شود و فرایند آن بدین ترتیب است:

1. در تمامی گره‌های تصمیم‌گیری پایانی (final decision nodes)، رفتار (action) بهینه را مشخص کنید.
2. با توجه به رفتارهای بهینه‌ای که در مرحلهٔ قبلی معین کردید، رفتار بهینه را در گره‌های تصمیم‌گیری یکی مانده به آخر تعیین کنید.
3. به همین ترتیب رفتارهای بهینه را به صورت معکوس در درخت بازی تعیین کنید.

توضیح بیشتر تعادل نش زیر بازی کامل و ارائه مثال

حال که با مفهوم استقرای معکوس آشنا شدید، به شرح بیشتر تعادل نش زیربازی کامل می پردازیم:

این شیوه از یافتن تعادل، توسط راینهارد سیلتن (Reinhard Selten) پیشنهاد شده‌است. در تعادل نش زیربازی کامل نباید هیچ زیربازی ای وجود داشته باشد که در آن، بازیکن i ام بتواند از طریق انتخاب استراتژی ای متفاوت از استراتژی s*_i، دریافتی خود را بیشتر کند، با توجه به اینکه هر بازیکن j دیگر، براساس استراتژی s*_j بازی می‌کند. بنابراین:

If:P(h)=i → u_i (O_h (S* ))≥ u_i(O_h (S_i,S_j* )) for ∀S_i

یعنی در تاریخچه‌ای که نوبت بازیکن iام است که استراتژی خود را انتخاب کند، مطلوبیتی که بازیکن iام از انتخاب استراتژی *S به دست می‌آورد، حداقل به خوبی مطلوبیتی است که از انتخاب هر استراتژی دیگری که متفاوت از استراتژی *S است، به دست می‌آورد، با توجه به اینکه سایر بازیکنان براساس استراتژی S*_j معین خود بازی می‌کنند.
فرایند استقرای معکوس می‌تواند در یافتن تعادل نش زیربازی کامل مورد استفاده قرار گیرد. انجام فرایند بدین ترتیب است:

1. تمام زیربازی‌های بازی کلی را پیدا کنید.
2. از انتهای درخت بازی شروع کرده و تعادل نش هر کدام از زیربازی‌های پایانی را بیابید.
3. هر کدام از زیربازی‌های پایانی را با پرداختی‌های تعادل نش آن زیربازی، جایگزین کرده و بدین ترتیب شکل کاهش یافتهٔ بازی را بسازید.
4. مراحل 2 و 3 را تکرار کنید و فرایند را ادامه دهید تا هر جابجایی (move) ترتیبی در بازی مشخص شود.
5. اگر هیچ‌کدام از زیربازی‌ها، تعادل نش چندگانه نداشته باشند، آن گاه تعادل نش زیربازی کامل مشخص شده، یکتا خواهد بود. درغیر اینصورت، فرایند مذکور را هر بار با جایگزین کردن یکی از تعادل‌های نش یافته شده ادامه دهید.

برای روشن تر شدن بیشتر این توضیحات، مثال بازی ورود به یک صنعت (شکل گستردهٔ بازی ورود به یک صنعت) را که پیش تر ذکر شد در نظر بگیرید؛ فرایند توضیح داده شده به ترتیب در آن انجام خواهد شد:

1. زیربازی‌های این بازی عبارتند از:

زیر بازی الف

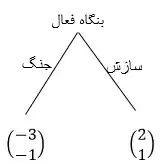
الف) (به شکل زیربازی الف توجه شود.)

ب) کل بازی

2. از زیربازی الف شروع می کنیم؛ در اینجا نوبت بنگاه فعال است که رفتار بهینه ی خود را انجام دهد و دریافتی‌های دوم (عدد پایینی) در ماتریس دریافتی‌ها (در شکل زیربازی الف) مربوط به او می‌باشد. بنگاه فعال با انتخاب استراتژی "جنگ"، دریافتی خود را برابر با 1- می‌کند درحالیکه اگر استراتژی "سازش" را اتخاذ کند، 1 نصیبش خواهد شد. بنابراین بنگاه فعال، استراتژی "سازش" را انتخاب خواهد کرد(زیرا 1> 1-).

3. شکل کاهش یافته ی بازی بدین ترتیب می‌شود(به "شکل کاهش یافته بازی" توجه شود):

شکل کاهش یافته بازی

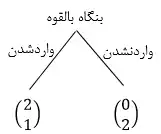
4. حال نوبت بنگاه بالقوه است که استراتژی بهینه ی خود را مشخص کند و دریافتی‌های اول در ماتریس دریافتی‌ها مربوط به این بنگاه است؛ بنگاه بالقوه با انتخاب استراتژی "وارد شدن"، دریافتی خود را برابر 2 خواهد کرد که بیشتر از دریافتی استراتژی "واردنشدن" است.

بدین ترتیب تعادل نش زیربازی کامل این بازی بدین ترتیب است:

(سازش اگر بنگاه بالقوه وارد بازار شود و وارد شدن)

لازم به ذکر است که هر تعادل نش زیربازی کامل، خود یک تعادل نش می‌باشد.

پس می‌توان گفت مجموعه تعادل‌های نش زیربازی کامل برای یک بازی گسترده متناهی با اطلاعات کامل برابر با مجموعه مشخصات استراتژی‌هایی است که از طریق فرایند استقرای معکوس به دست آمده‌است.
همچنین هر بازی متناهی با اطلاعات کامل یک استراتژی خالص تعادل نش زیربازی کامل دارد. علاوه براین، اگر هیچ بازیکنی پرداختی مشابه در هر دو گره پایانی نداشته باشد، پس یک تعادل نش زیربازی کامل یکتا وجود خواهد داشت.

بازی اولتیماتوم

حال به شرح معروف‌ترین مثال یافتن تعادل نش زیربازی کامل، یعنی "بازی اولتیماتوم" می پردازیم:
فرض کنید 10000 تومان پول وجود دارد. بازیکن 1 که "پیشنهاد دهنده" است، باید x تومان را به بازیکن 2 پیشنهاد دهد. X بین صفر تا 10000 تومان می‌تواند تغییر کند و کمترین واحد آن 100 تومان است. بازیکن 2 که "پاسخ دهنده" است، می‌تواند "بله" یا "خیر" را انتخاب کند. اگر "بله" را انتخاب کند، پرداختی به وی برابر با x و پرداختی به بازیکن 1 برابر با اختلاف ده هزار و عدد پیشنهادی خواهد شد؛ و اگر "خیر" را انتخاب کند، پرداختی به هر دوی آن‌ها برابر با صفر خواهد بود. فرض می‌شود هر بازیکن تنها به دریافتی خودش توجه دارد. شکل گسترده این بازی بدین ترتیب است:

شکل گسترده بازی اولتیماتوم

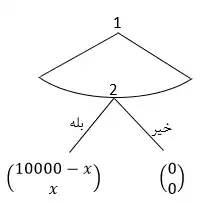
از طریق استقرای معکوس به یافتن تعادل نش زیربازی کامل بازی مذکور می پردازیم:
در زیربازی پایانی بازیکن 2 باید تصمیم بگیرد که استراتژی "بله" را انتخاب کند یا "خیر"؛ اگر x>0 به بازیکن 2 پیشنهاد شود، برای بازیکن 2 اکیداً بهینه است که "بله" را انتخاب کند. اگر به بازیکن 2، x=0 پیشنهاد شود، او بین بازی کردن "بله" یا "خیر" بی‌تفاوت است.

• یک تعادل نش زیربازی کامل برای این بازی بدین ترتیب است:

بازیکن 2 اگر x>0 به وی پیشنهاد شود، "بله" را انتخاب می‌کند، و اگر x=0 به او پیشنهاد شود، "خیر" را بازی می‌کند.
در این صورت برای بازیکن 1 بهینه است که x=100 تومان را به بازیکن 2 پیشنهاد دهد؛ درحقیقت، چون تقریباً همهٔ قدرت چانه زنی دست بازیکن 1 است، او تقریباً همهٔ پول را برای خود برمی دارد.

• یک تعادل نش زیربازی کامل دیگر این بازی چنین است که:
  

بازیکن 2 به ازای هر x ای که به وی پیشنهاد شود، "بله" را بازی می‌کند. در این شرایط برای بازیکن 1، بهینه این است که x=0 را به بازیکن 2 پیشنهاد دهد.

- اما تحقیقات تجربی نشان داده است که:

بازیکن 1 معمولاً 35 تا 50 درصد از پول را به بازیکن 2 پیشنهاد می‌دهد.
بازیکن 2 پیشنهادهای کوچک را رد می‌کند.
علت این امر دو چیز می‌تواند باشد: ممکن است بازیکن 2 نسبت به برابری حساس باشد و دوست نداشته باشد که با او ناعادلانه رفتار شود؛ به همین دلیل پیشنهادهای کم را رد می‌کند. ممکن است که بازیکن 1 نسبت به برابری حساس باشد و دوست نداشته باشد که با بازیکن 2 با نابرابری رفتار کند؛ یا حتی با علم به اینکه بازیکن 2 پیشنهادهای کم را رد می‌کند، سعی در بهینه کردن دریافت پولی خود داشته باشد.

پانویس

1. Osborne, M. J. (2004). An Introduction to Game Theory. Oxford University Press.

منابع

• Osborne, M. J. (2004). An Introduction to Game Theory. Oxford University Press
• Mass-Collel. (1995). Microeconomic Theory. Oxford University Press

• مشارکت‌کنندگان ویکی‌پدیا. «spne». در دانشنامهٔ ویکی‌پدیای انگلیسی.