سهمی‌گون

در هندسهٔ تحلیلی، سهمی‌گون (به انگلیسی: Paraboloid) یک رویه و از انواع رویه‌های درجهٔ دوم است[1].

سهمی‌گون هذلولوی (راست) و سهمی‌گون بیضوی (چپ)شکل وسط یک استوانهٔ سهموی ست و سهمی‌گون نیست (سطح استوانه‌ای ست).

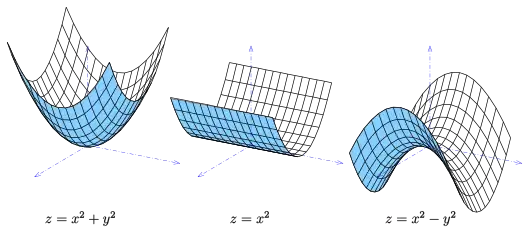
سهمی‌گون بیضوی دورانی حالت خاصی از سهمی‌گون است که از دوران یک سهمی حول محور تقارن آن به دست می‌آید.

سهمی‌گون به دو دستهٔ بیضَوی و سهمی‌گون هُذلولَوی تقسیم می‌شود. سهمی‌گون هذلولوی شکلی مشابه زین اسب دارد.

معادلهٔ استاندارد

سهمی‌گون بیضوی

در دستگاه مختصات دکارتی، روش استاندارد نمایش یک سهمیی‌گون بیضوی با رأس در مبدأ مختصات به صورت زیر است[1]:

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}={z \over c}}$

اگر ${\displaystyle a=b}$ باشد سهمی‌گون دایروی یا سهمی‌گون دورانی حاصل می‌شود.

سهمی‌گون هذلولوی

در دستگاه مختصات دکارتی، روش استاندارد نمایش یک سهمیی‌گون هذلولوی به صورت زیر است[1]:

${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}={z \over c},\quad c>0}$

استوانهٔ سهموی

با این که استوانهٔ سهموی یک سهمی‌گون نیست، به دلیل شباهتش با هر دو نوع سهمی‌گون، در این نوشتار به آن اشاره می‌شود.

اگر ${\displaystyle b\rightarrow \infty }$، به فرمول استوانهٔ سهموی می‌رسیم:

${\displaystyle z=ax^{2},y\in \mathbb {R} }$

در ابعاد بالاتر

یک ابرسهمی‌گون در فضای ${\displaystyle \mathbb {R} ^{n}}$، یک ابررویهٔ درجه دو است. یک ابرسهمی‌گون، همهٔ نقاطی مانند ${\displaystyle P=(x_{1},x_{2},\dots ,x_{n})}$ است که در معادلهٔ استاندارد زیر صدق کنند:

${\displaystyle \pm {x_{1}^{2} \over c_{1}^{2}}\pm {x_{2}^{2} \over c_{2}^{2}}\pm \dots \pm {x_{n-1}^{2} \over c_{n-1}^{2}}={x_{n} \over c_{n}}}$

ویژگی بازتابندگی

سهمی‌گون دایروی یک کانون دارد. هر شعاع نوری که از کانون آن به بدنهٔ سهمی‌گون بتابد، بازتاب آن موازی با محور تقارن سهمی‌گون بازخواهد گشت؛ و برعکس، هر شعاع نوری که موازی با محور تقارن سهمی‌گون به بدنهٔ سهمی‌گون بتابد، بازتاب آن از کانون سهمی‌گون خواهد گذشت[2].

از این خاصیت در ابزار‌های نورانی‌کردن مثل چراغ جلوی خودروها، پروژکتورها و ... استفاده می‌شود.

همچنین از این ویژگی در ابزارهای دریافت امواج مثل دیش‌های ماهواره استفاده می‌شود.

در طبیعت

سهمی‌گون هذلولوی در برگ گیاهان و در ساختار چیپس دیده می‌شود.

جستارهای وابسته

• سهمی
• رویه
• رویهٔ درجهٔ دوم

منابع

1. «۱۲٫۶». Thomas' Calculus (14th Edition).
2. «۲: آشنایی با مقاطع مخروطی». هندسه ۳ (آموزش و پرورش).