ریاضیات و معماری

ریاضیات و معماری مرتبط هستند، معماری مانند دیگر هنرها از ریاضیات بهره می‌برد. به‌جز استفاده از ریاضیات برای مهندسی ساختمان‌ها، معماری از هندسه برای تعریف فرم فضایی یک ساختمان استفاده می‌کند؛ از زمان مکتب فیثاغوری در سده ششم پیش از میلاد به بعد، تا فرم‌هایی هماهنگ و دارای هارمونی خلق کند، و بدین ترتیب ساختمان‌ها و محیط اطرافشان را بر طبق اصول مذهبی و زیبایی‌شناسی ریاضیاتی نظم ببخشد، مانند تزئین ساختمان با اشیاء ریاضیاتی مانند مفروش‌سازی یا برای سازگاری با محیط زیست مانند کاهش سرعت باد در پای یک ساختمان بلند.

برج تبر سنت ماری ۳۰،[1] در لندن یک جسم دوران یافته دارای طراحی پارامتریک است.
معبد کندریه ماهادوا (حدود ۱۰۳۰) در خاجوراهو، هند، نمونه ای از معماری مذهبی با ساختار فرکتال مانند است که دارای قسمتهای زیادی شبیه کل است.[2]

در مصر باستان، یونان باستان، هند و دنیای اسلام ساختمان‌هایی مانند اهرام، معابد، مساجد، قصرها و آرامگاه‌های یادمانی برای مقاصد مذهبی با تناسبات خاص ساخته‌می‌شدند. در معماری اسلامی نمای بیرونی و داخلی بنا را با اشکال هندسی و الگوهای هندسی اسلامی تزئین می‌کنند. برخی از معابد هندوها ساختار فراکتال مانند دارند که در آن‌ها بخش‌هایی با کل همانند هستند که مفهوم بی‌نهایت در کیهان‌شناسی هندو را نشان می‌دهد. در معماری چینی تولوهای فوجیان و سازه‌ای دفاعی دایره‌ای هستند. در سده بیست و یکم استفاده از ریاضیات در طراحی ساختمان‌های عمومی بار دیگر مورد توجه قرار گرفته‌است.

در معماری رنسانس معمارانی مانند لئون باتیستا آلبرتی، سباستیانو سرلیو و آندرا پالادیو تحت تأثیر در باب معماری اثر ویترویوس از روم باستان و فیثاغورث از یونان باستان به تقارن و تناسب به عمد تأکید می‌کردند. در پایان سده نوزدهم ولادیمیر شوخوف در روسیه و آنتونی گائودی از بارسلون پیشگامان استفاده از سازه هذلولی‌وار بودند، گائودی در ساخت ساگرادا فامیلیا از هذلولی سهمی‌گون، موزاییک کاری، طاق زنجیروار، زنجیره وار، پیچوار و سطح خط‌دار استفاده کرد. سبک‌های نو در سده بیستم میلادی مانند معماری مدرن و ساختارشکنی برای دست‌یابی به اثرات مطلوب از هندسه‌های متفاوت کمک گرفتند. از رویهٔ مینیمال برای ساخت سقف‌های خیمه مانند استفاده شده‌است مانند فرودگاه بین‌المللی دنور. در این دوره باکمینستر فولر گنبد ژئودزیک را ابداع کرد.

رشته‌های مرتبط
در دوره رنسانس انتظار می‌رفت که معماری مانند لئون باتیستا آلبرتی در بسیاری از رشته‌ها از جمله حساب و هندسه دانش داشته باشد.

معماران مایکل استوالد و کیم ویلیامز، درمورد رابطه بین معماری و ریاضیات استدلال می‌کنند که این دو رشته اروپای دوران قدیم قویا به هم مرتبط هستند اما خاطرنشان می‌کنند که این دو رشته تا آنجا که به‌صورت عامیانه فهمیده می‌شوند شاید به‌نظر بیاید که رابطه ضعیفی دارند زیرا معماری حرفه‌ای است که بر ساخت ساختمان تمرکز دارد، درحالی که ریاضیات اعداد و دیگر موضوعات انتزاعی را مطالعه می‌کند. ویترویوس یک معمار را فردی می‌دانست که به اندازه کافی از دامنه‌ای از دیگر رشته‌ها، مخصوصاً هندسه، اطلاع داشته باشد تا بتواند بر کار دیگر صنعتگران حرفه‌ای در دیگر رشته‌ها مانند سنگتراشی و نجاری نظارت کند. در قرون وسطی نیز همین موارد رعایت می‌شد، دانشجویان حساب، هندسه و زیبایی‌شناسی را درکنار گرامر، منطق و بلاغت (تریوییم) را در تالارهایی می‌آموختند که توسط استاد سازنده‌ای طراحی شده بود که خود صنعتگران دیگری را آموزش می‌دادند. یک استاد سازنده در بالاترین مرتبه عنوان معمار یا مهندس می‌گرفت. در رنسانس علوم اربعه نیز به جمع علومی که یک همه‌چیزدان باید می‌دانست اضافه شدند. لئون باتیستا آلبرتی و کریستوفر رن که امروزه به عنوان معمار شناخته می‌شوند در ابتدا با عنوان ستاره‌شناس یاد می‌شدند.[3]

ویلیامز و استوالد با مرور بیشتر تعامل ریاضیات و معماری از سال ۱۵۰۰ با توجه به رویکرد جامعه‌شناس آلمانی تئودور آدورنو، سه گرایش را در بین معماران شناسایی می‌کنند، یعنی: انقلابی بودن، معرفی ایده‌های کاملاً جدید؛ ارتجاعی بودن، عدم ایجاد تغییر؛ یا باززنده سازی، در واقع به عقب بازمی‌گردند. آنها استدلال می‌کنند که معماران در دوران باززنده سازی از الهام گرفتن از ریاضیات پرهیز کرده‌اند. این توضیح می‌دهد که چرا در دوره‌های باززنده سازی، مانند معماری نئوگوتیک در قرن نوزدهم در انگلیس، معماری ارتباط کمی با ریاضیات داشت. به همین ترتیب، آنها متذکر می‌شوند که دردوره‌های باززنده سازی مانند تکلف‌گرایی در ایتالیا در حدود ۱۵۲۰ تا ۱۵۸۰، یا جنبش‌های باروک و پالادیان در قرن هفدهم، ریاضیات به ندرت مورد توجه قرار می‌گرفت. در مقابل، جنبش‌های انقلابی اوایل قرن بیستم مانند فوتوریسم و ساخت‌گرایی به‌طور فعالانه عقاید قدیمی را رد می‌کردند، به ریاضیات توجه می‌کردند و به سوی معماری نوگرا پیش می‌رفتند. همچنین در اواخر قرن بیستم، هندسه فراکتال و همچنین کاشی کاری غیر دوره ای به سرعت توسط معماران پذیرفته شد.[4]

به غیر از استفاده از ریاضیات برای مهندسی ساختمان، معماران به چند دلیل از ریاضیات استفاده می‌کنند.[5] اول، آنها از هندسه برای تعریف فرم فضایی ساختمان استفاده می‌کنند.[6] دوم، آنها از ریاضیات برای طراحی فرم‌هایی استفاده می‌کنند که زیبا یا هماهنگ به نظر می‌رسند.[7] از زمان مکتب فیثاغوری،[8] معماران در یونان باستان، روم باستان، جهان اسلام و رنسانس ایتالیایی تناسبات محیط ساخت - ساختمانها و محیط طراحی شده اطراف آنها - را با مد نظر قرار دادن ریاضیات، اصول زیبایی شناختی و گاه مذهبی برمی‌گزیدند.[9][10][11][12] سوم، آنها ممکن است از اشیا ریاضیاتی مانند مفروش‌سازی برای تزئین ساختمان استفاده کنند.[13][14] چهارم، آنها می‌توانند از ریاضیات در مدلسازی رایانه ای برای دستیابی به اهداف زیست‌محیطی استفاده کنند، مثلاً جریان‌های هوای پایه ساختمان‌های بلند را به حداقل برسانند.[1]

زیبایی‌شناسی سکولار

رم باستان
پلان یک خانه رومی از ویتروویوس

ویترویوس
اطلاعات بیشتر: ویتروویوس و در باب معماری
فضای داخلی پانتئون، ۱۷۵۸

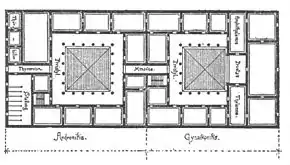
به گفته ویترویوس طراحی یک ساختمان مانند معبد به دو کیفیت نسبت و تقارن بستگی دارد. تناسب باعث می‌شود هر قسمت از یک ساختمان ارتباط هماهنگ با دیگر بخش‌ها داشته باشد. منظور ویترویوس از تقارن بیشتر به مفهوم مدولار نزدیک است تا تقارن محوری و به معنی اتصال بخش‌ها (مدولار) به‌یکدیگر برای ایجاد یک ساختمان است. او در باسیلیکا فانو از نسبت‌های صحیح کوچک، به ویژه اعداد مثلثی (۱، ۳، ۶، ۱۰ ، ...) برای تناسب بخشیدن به ساختمان بر طبق مدول (ویترویوسی) استفاده کرد؛ بنابراین نسبت عرض باسیلیکا به طول آن ۱/۲ است. ارتفاع راهرو اطراف آن به اندازه عرض راهرو است، ۱/۱؛ ستون‌ها ۵ فوت ضخامت و پنجاه فوت ارتفاع دارند، ۱/۱۰.[9]

پلان همکف پانتئون

ویترویوس سه ویژگی مورد نیاز برای معماری را در کتاب در باب معماری نام برده‌است. آن سه ویژگی عبارت‌اند از: استحکام ، سودمندی و لذت. این ویژگی‌ها می‌توانند به عنوان دسته‌بندی برای طبقه‌بندی روش‌های استفاده از ریاضیات در معماری استفاده شوند. استحکام به معنی استفاده از ریاضیات برای اطمینان حاصل کردن از ایستادگی ساختمان است، از این رو ابزارهای ریاضی در طراحی مورد استفاده قرار می‌گیرند. سودمندی تا حدی ناشی از کاربرد مؤثر ریاضیات است و باید روابط فضایی و روابط دیگر در یک طرح تحلیل و استدلال شوند. لذت صفتی از ساختمان است که از دربرداشتن روابط ریاضی در ساختمان حاصل می‌شود. لذت شامل ویژگی‌های زیبایی شناختی، عاطفی و ذهنی است.[15]

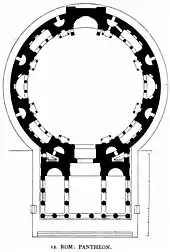
پانتئون
نوشتار اصلی: پانتئون (معبد رومی)

پانتئون در رم ساختار کلاسیک، تناسب و تزئین رومی را به تصویر می‌کشد. ساختار اصلی یک گنبد است، گنبد بنا یک حفره مرکزی بازدارد که اجازه ورود نور به فضای داخل را می‌دهد. مقابل آن یک ردیف ستون کوتاه با سنتوری سه‌گوش قرار دارد. ارتفاع تا حفره مرکزی باز گنبد با قطر دایره داخلی یکسان است، ۴۳٫۳ متر (۱۴۲ فوت)، بنابراین کل فضای داخلی دقیقاً درون یک مکعب قرار می‌گیرد و فضای داخلی می‌تواند کره‌ای با همان قطر را در خود جای دهد.[16] این ابعاد وقتی در واحدهای اندازه‌گیری روم باستان بیان می‌شوند، معنا بیشتری پیدا می‌کنند: گنبد به طول ۱۵۰ فوت رومی[persian-alpha 1] است. قطر پوسته ۳۰ فوت رومی است. ارتفاع درگاه ۴۰ فوت رومی است.[17] پانتئون بزرگترین گنبد بتونی مسلح نشده جهان است.[18]

رنسانس
اطلاعات بیشتر: معماری رنسانس
نمای باسیلیکای سنت ماریا نولا، ۱۴۷۰، حاشیه زینتی (تزئین شده با مربع) و بالای آن از لئون باتیستا آلبرتی است.

کتاب در هنر ساختمان از لئون باتیستا آلبرتی اولین رساله معماری در دوره رنسانس است. این کتاب در سال ۱۴۸۵ چاپ شد و اولین کتاب چاپ شده در زمینه معماری بود. این کتاب تا حدودی بر پایه کتاب در باب معماری از ویترویوس، نیکوخاموس و حساب فیثاغورس نوشته شده‌است. آلبرتی از یک مکعب شروع می‌کند و از آن نسبت می‌گیرد؛ بنابراین قطر یکی از سطح‌های مکعب نسبت ۲√:۱ و قطر کره ای که مکعب را احاطه می‌کند نسبت ۳√:۱ دارد.[19][20] آلبرتی همچنین کشف فیلیپو برونلسکی در مورد پرسپکتیو خطی را مستند ساخت که امکان طراحی ساختمان‌هایی را می‌دهد که اگر از فاصله مناسب دیده شوند متناسب و زیبا دیده خواهند شد.[12]

یک پرسپکتیو معماری از سباستیانو سرلیو.[21]

متن مهم بعدی در باب معماری کتاب قواعد عمومی معماری (Regole generali d'architettura) از سباستیانو سرلیو بود. جلد اول این کتاب در ونیز در سال ۱۵۳۷ نگاشته شد. جلد ۱۵۴۵ (کتاب‌های ۱ و ۲) به هندسه و پرسپکتیو می‌پردازد. دو تا از روش‌های سرلیو برای ایجاد پرسپکتیو اشتباه بود، اما این باعث توقف استفاده گسترده از کار وی نشد.[22]

پلان و نمای ویلای پیسانی از آندره پالادیو.

آندره پالادیو کتاب تأثیرگذار چهار کتاب معماری را در سال ۱۵۷۰ در ونیز منتشر کرد. این کتاب که به‌طور گسترده چاپ شد تا حد زیادی عامل اشاعه اندیشه‌های رنسانس ایتالیا در سرتاسر اروپا بود. هنری ووتون، دیپلمات انگلیسی، از طرفداران این کتاب بود و با کتاب عناصر معماری خود به تکامل آن کمک کرد.[23] نسبت‌ها هر فضای داخل ویلا با نسبت‌های ساده ریاضی مانند ۳: ۴ و ۴: ۵ محاسبه می‌شد و فضاهای مختلف داخل خانه با این نسبت‌ها به هم پیوند داده می‌شدند. معماران قبلی از این فرمول‌ها برای ایجاد تعادل در یک نمای متقارن استفاده می‌کردند. معمولاً طرح‌های پالادیو مربع شکل است.[24] پالادیو در چهار کتاب معماری طیف وسیعی از نسبت‌ها را مجاز دانست و اظهار داشت:[25][26]

هفت نوع فضا وجود دارد که زیباترین و دارای تناسبات خوب هستند و بهتر در می‌آیند: می‌توانند مدور ساخته شوند؛ اگرچه نادر است؛ یا مربع شکل؛ یا طولشان با با قطر مربع عرض برابر باشد؛ یا یک مربع و یک سوم؛ یا یک مربع و نصف؛ یا یک مربع و دو سوم؛ یا دو مربع.

وینچنزو اسکاموزی رساله ایده یک معماری جهانی (L'idea dell'architettura universale) را در سال ۱۶۱۵منتشر کرد.[27] او تلاش کرد تا طراحی شهرها و ساختمانها را به ایده‌های ویتروویوس و فیثاغورث و ایده‌های اخیر پالادیو مرتبط کند.[28]

قرن نوزدهم
فانوس دریایی هذلولی‌وار اثر ولادیمیر شوخوف، اوکراین، ۱۹۱۱

در اواخر قرن نوزدهم ولادیمیر شوخوف از سازه هذلولی‌وار برای ساخت دکل‌ها، فانوس‌های دریایی و برج‌های خنک‌کننده استفاده کرد. این سازه‌ها زیبا و پایدار هستند و از مصالح ساختمانی اقتصادی در ساخت آن‌ها استفاده می‌شود. اولین برج هذلولی‌وار شوخوف در سال ۱۸۹۶ در نیژنی نووگورود به نمایش گذاشته شد.[29][30][31]

قرن بیستم
اطلاعات بیشتر: معماری مدرن
سطوح متقاطع سبک د استایل: خانه ریتفلد شرودر، ۱۹۲۴

جنبش معماری مدرن که ساخت‌گرایی روسی پیشگام آن بود و در اویل سده بیستم پا گرفت[32] از هندسه راست خط اقلیدسی (که دکارتی نیز نامیده می‌شود) استفاده کرد. در جنبش د استایل از خطوط افقی و عمودی استفاده شد. در جنبش د استایل فرم‌های معماری از کنار هم گذاشتن این دو محور حاصل می‌شوند و سطوح سقف، صفحات دیوار و بالکن‌ها یکدیگر را قطع می‌کنند یا از کنار هم می‌گذرند. مانند خانه ریتفلد شرودر که توسط گریت ریتفلد در سال ۱۹۲۴ طراحی شده‌است.[33]

طراحی شقایق و فلفل‌دان (زیست‌تقلید) از رائول هاینریش فرانس، ۱۹۲۰

معماران مدرنیست در استفاده از منحنی نیز آزاد بودند. ایستگاه متروی آرنوس گرو که توسط چارلز هولدن در سال ۱۹۳۳ طراحی شد، یک سالن فروش بلیط دایره ای شکل آجری با سقف مسطح بتنی دارد.[34] در سال ۱۹۳۸ لاسلو موهولی-ناگی هفت عنصر زیست‌تقلید رائول هاینریش فرانس را به عنوان اجزای سازنده اساسی معماری الهام گرفته از طبیعت اتخاذ کرد. این هفت عنصر کریستال، کره، مخروط، سطح، نوار (مکعبی)، میله (استوانه‌ای)، و مارپیچ هستند.[35][36]

لو کوربوزیه یک مقیاس آنتروپومتری از تناسبات در معماری را ارائه کرده‌است. این مقیاس مدولار نام دارد و برپایه قد انسان مذکر است.[37] لوکوربوزیه در سال ۱۹۵۵ در کلیسای رونشان از منحنی‌های فرم آزاد استفاده کرد که با فرمول‌های ریاضی قابل توصیف نیست. گفته می‌شود او از اشکال طبیعی مانند دماغه کشتی یا دست‌های درحال دعا ایده گرفته‌است.[38] طراحی فقط در بزرگترین مقیاس است: هیچ سلسله مراتبی از جزئیات در مقیاسهای کوچکتر وجود ندارد و بنابراین هیچ بعد فراکتالی وجود ندارد. این مورد در مورد سایر بناهای معروف قرن بیستم مانند تالار اپرای سیدنی، فرودگاه بین‌المللی دنور و موزه گوگنهایم بیلبائو صدق می‌کند.[39]

از نظر ۹۰ معمار برجسته که به نظرسنجی جهانی معماری در سال ۲۰۱۰ پاسخ دادند، معماری معاصر بسیار متنوع است. موزه گوگنهایم از فرانک گری بهترین کار ارزیابی شد.[40]

رویه مینیمال سقف پارچه‌ای فرودگاه بین‌المللی دنور از رشته‌کوه‌های برفی کلرادو و چادر سرخ‌پوستان بومی آمریکا ایده گرفته‌است.

باکمینستر فولر به دلیل طراحی سازه‌های پوسته نازک قوی معروف به گنبدهای ژئودزیک مشهور است. گنبد مونترال بایوسفر ۶۱ متر (۲۰۰ فوت) ارتفاع دارد و قطر آن ۷۶ متر (۲۴۹ فوت) است.[41]

سقف پارچه ای ساختمان فرودگاه بین‌المللی دنور یک رویه مینیمال است (یعنی خمیدگی میانگین آن صفر است) و توسط کابل‌های فولادی پشتیبانی می‌شود. این ساختمان کوه‌های برفی کلرادو و چادرهای بومیان آمریکا را تداعی می‌کند.[42][43]

سقف خانه اپرای سیدنی از طاقهای سفید سر به فلک کشیده تشکیل شده‌است و یادآور بادبان کشتی است. برای ساخت آنها تمام طاقها از بخشهای مثلثی پوسته‌های کروی با شعاع یکسان تشکیل شده‌اند. اینها در هر جهت دارای انحنای یکنواخت لازم هستند.[44]

جنبش ساختارشکنی در اواخر قرن بیستم بی‌نظمی‌های حساب‌شده ایجاد می‌کند. نیکوس سالینگاروس در A Theory of Architecture از این موضوع با عنوان فرم‌های تصادفی[45] با پیچیدگی بالا[46] یاد می‌کند که در آن از دیوارهای غیر موازی، شبکه‌های روی هم قرار داده شده و سطوح پیچیده دوبعدی استفاده شده‌است، نظیر آنچه در تالار کنسرت والت دیزنی از فرانک گری و موزه گوگنهایم وجود دارد.[47][48] تا قرن بیستم، دانشجویان معماری موظف بودند زمینه ای در ریاضیات داشته باشند. سالینگاروس استدلال می‌کند که ابتدا مدرنیسم بیش از حد ساده انگارانه دارای انگیزه‌های سیاسی و سپس ساختارشکنی ضد علمی، معماری را از ریاضیات جدا کرده‌است. او معتقد است که این برگشت از ارزشهای ریاضی مضر است، زیرا زیبایی‌شناسی فراگیر معماری غیر ریاضیاتی به مردم می‌آموزد تا اطلاعات ریاضیاتی در محیط را پس بزنند. او استدلال می‌کند که این تأثیرات منفی بر جامعه دارد.[39]

اصول دینی

مصر باستان
نسبت قاعده به وتر (b:a) برای هرم بزرگ جیزه می‌تواند فی:۱ (مثلث کپلر)، ۳:۵ (مثلث ۳:۴:۵) یا ۱:۴⁄۳/۱۴ باشد.

اهرام مصر باستان مقبره‌هایی هستند که با تناسبات ریاضی ساخته شده‌اند، اما اینکه از چه تناسباتی استفاده شده و اینکه آیا قضیه فیثاغورث استفاده شده‌است یا خیر، مورد بحث است. نسبت ارتفاع جانبی به نصف طول قاعده هرم بزرگ جیزه کمتر از ۱٪ از نسبت طلایی است.[49] اگر شیوه طراحی این بود باید از مثلث کپلر استفاده می‌شد (زاویه سطح '۴۹ °۵۱)،[49][50] اما به گفته بسیاری از مورخان، نسبت طلایی تا زمان مکتب فیثاغوری شناخته شده نبود.[51] هرم بزرگ ممکن است بر اساس یک مثلث با نسبت قاعده به ارتفاع ۱:۴⁄۳/۱۴ ساخته شده باشد (زاویه سطح '۵۰ °۵۱).[52]

نسبت برخی از اهرام نیز ممکن است بر اساس مثلث ۵:۴:۳ (زاویه سطح '۸ °۵۳) باشد، که از زمان پاپیروس ریاضی ریند شناخته شده‌است (۱۶۵۰–۱۵۵۰ قبل از میلاد مسیح)؛ اولین بار در سال ۱۸۸۲ موریتس کانتور به این موضوع پی برد.[53] مشخص شده‌است که در مصر باستان زاویه‌های راست با دقت با استفاده از طناب‌های گره دار اندازه گذاری و سپس ساخته می‌شدند.[53] پلوتارک در ایسیس و اوزیریس (۱۰۰ بعد از میلاد) ثبت کرده‌است که مصریان مثلث ۵:۴:۳ را تحسین می‌کردند.[53] و یک طومار مربوط به سال ۱۷۰۰ قبل از میلاد فرمولهای اساسی مربع را شرح داده‌است.[54] راجر ال. کوک می‌گوید «تصور اینکه کسی بدون آگاهی از قضیه فیثاغورث به این تناسبات علاقه داشته باشد دشوار است»، اما همچنین اشاره می‌کند که هیچ متن مصری قبل از ۳۰۰ قبل از میلاد استفاده از قضیه فیثاغورث را برای یافتن طول اضلاع مثلث ذکر نمی‌کند و روشهای ساده‌تری برای ساخت زاویه قائم وجود داشته. کوک حدس می‌زند که مصریان باستان احتمالاً قضیه فیثاغورس را می‌دانسته‌اند، اما هیچ مدرکی وجود ندارد که آنها از آن برای ساختن زاویه‌های قائم استفاده می‌کردند.[53]

هند باستان
اطلاعات بیشتر: معماری هندی
گوپورام معبد ویروپاکشا دارای ساختار فراکتال مانند است.

واستو شسترا (vāstu śāstra)، قوانین معماری و شهرسازی هند باستان، نقشه‌های متقارنی معروف به ماندالا را به‌کار می‌برد. از محاسبات پیچیده برای رسیدن به ابعاد ساختمان و اجزای سازنده آن استفاده می‌شود. این طرح‌ها با هدف تلفیق معماری با طبیعت، عملکردهای نسبی قسمت‌های مختلف سازه و اعتقادات باستانی با استفاده از الگوهای هندسی (یانترا)، تقارن و ترازهای جهت دار نظر گرفته شده‌اند.[55][56] سازندگان هندی ممکن است به‌طور تصادفی به نسبت‌های ریاضی رسیده باشند. به باور جورج ایفرا ریاضی‌دان می‌توان با ترفندها و ابزارهای ساده مانند رشته و میخ اشکال هندسی مانند بیضی و زاویه‌های راست گوشه رسم کرد.[12][57]

پلان معبد میناکشی در مادورای، از قرن هفتم به بعد. چهار دروازه (شماره‌هایI تا IV) گوپورام هستند.

استفاده از ریاضیات فراکتال سبب شده ساختمانهای موجود از جذابیت جهانی برخوردار باشند و از نظر بصری نیز احساس رضایت در بیننده ایجاد کنند زیرا در فواصل دید مختلف به بیننده احساس مقیاس القا می‌کنند. برای مثال، در گوپورام‌های بلند معابد هندو مانند معبد ویروپاکشا در هامپی و کاندریا ماهادو در خاجوراهو اجزا و کل دارای خصوصیات یکسان هستند و بعد فراکتالی آن‌ها در محدوده ۱٫۷ تا ۱٫۸ است. شبکه برجهای کوچکتر (شیخارا، کوه روشن) که بلندترین و مرکزی‌ترین برج است و نماد کوه کایلاش، اقامتگاه شیوا، است و تکرار بی پایان جهان در کیهان‌شناسی هندو را به تصویر می‌کشد.[2][58]

معبد میناکشی امان در شهر مادورای یک مجتمع بزرگ دارای زیارتگاه‌های متعدد است و خیابان‌های شهر مادورای به‌صورت متحدالمرکز دور آن ساخته شده‌اند. چهار دروازه بلند آن (گوپورام) با ساختار تکرار شونده فراکتال ساخته شده‌اند. محدوده‌های‌های اطراف هر زیارتگاه مستطیل شکل است و با دیوارهای سنگی بلند ساخته شده‌است.[59]

یونان باستان
اطلاعات بیشتر: معماری یونان باستان، نسبت طلایی، مکتب فیثاغوری، و هندسه اقلیدسی
پارتنون با تناسبات فیثاغورسی ساخته شده‌است.

فیثاغورس (حدود ۵۶۹ - حدود ۴۷۵ پیش از میلاد) و پیروانش معتقد بودند «همه چیز اعداد هستند». آنها هارمونی‌های تولید شده توسط نت‌ها با فرکانس‌های دارای نسبتهای کوچک صحیح را مشاهده کردند و استدلال کردند که ساختمانها نیز باید با چنین نسبتهایی طراحی شوند. کلمه یونانی Symmetria در اصل نشان دهنده هارمونی اشکال معماری با نسبت‌های دقیق از کوچکترین جزئیات ساختمان تا کل طراحی آن است.[12]

پارتنون دارای ۶۹٫۵ متر (۲۲۸ فوت) طول، ۳۰٫۹ متر (۱۰۱ فوت) عرض و ۱۳٫۷ متر (۴۵ فوت) ارتفاع تا قرنیز است؛ بنابراین نسبت عرض به طول ۴:۹ است. نسبت ارتفاع به عرض نیز همین است. اگر این نسبت‌ها را کنار هم قرار دهیم نسبت ارتفاع:عرض:طول ۱۶:۳۶:۸۱ یا[60] ۴۲:۶۲:۹۲ خواهد بود پس مدول آن ۰٫۸۵۸ است. یک مستطیل با نسبت ۴:۹ را می‌توان با سه مستطیل مجاور با نسبت ۳:۴ ساخت. سپس هر نیم مستطیل یک مثلث ۳:۴:۵ است؛ بنابراین می‌توان زوایا و اضلاع را با یک طناب گره خورده بررسی کرد. مساحت داخلی (درون‌خانه) نیز به همین ترتیب دارای نسبت ۴:۹ است (۲۱٫۴۴ متر (۷۰٫۳ فوت) عرض و ۴۸٫۳ متر طول)؛ نسبت بین قطر ستون‌های بیرونی، ۱٫۹۰۵ متر (۶٫۲۵ فوت)، و فاصله مراکز آنها، ۴٫۲۹۳ متر (۱۴٫۰۸ فوت)، نیز ۴:۹ است.[12]

پلان همکف پارتنون

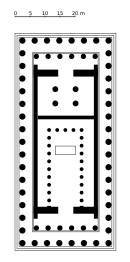
پارتنون توسط نویسندگانی مانند جان ژولیس نوریچ «عالی‌ترین معبد دوریک ساخته شده» قلمداد می‌شود.[61] از ریزه سازی‌های معماری استادانه آن می‌توان به تشابه ظریف بین انحنای روپی، باریک شدن دیوارهای درون‌خانه و میان کوژی ستون‌ها اشاره کرد.[61] میان کوژی کوژی کمی است که به وسط ستون می‌دهند یا به عبارت دیگر به کاهش قطر ستون‌ها در هنگام بالا آمدن اشاره دارد. روپی سکویی است که ستون‌ها بر روی آن قرار می‌گیرند. همانند سایر معابد کلاسیک یونان،[62] سکو دارای انحنای سهموی اندکی به سمت بالا برای هدایت آب باران و تقویت ساختمان در برابر زلزله است؛ بنابراین ممکن است ستون‌ها به سمت بیرون متمایل شوند، اما در واقع ستون‌ها کمی به سمت داخل متمایل اند و در صورت ادامه دادن آن‌ها به سمت بالا، حدود یک کیلومتر و نیم بالاتر از مرکز ساختمان قرار می‌گیرند. از آنجا که ارتفاع همه ستون‌ها یکسان است، انحنای لبه بیرونی روپی به فرسب و سقف بالای آن منتقل می‌شود: «همه از قانون ساخته شدن برای انحناهای ظریف پیروی می‌کنند».[63]

نسبت طلایی در ۳۰۰ سال قبل از میلاد پس از اینکه که اقلیدس روش ساخت هندسی را توصیف کرد، شناخته شد.[64] گفته شده‌است که از نسبت طلایی در طراحی پارتنون و دیگر بناهای یونان باستان و همچنین مجسمه‌ها، نقاشی‌ها و گلدان‌ها استفاده شده‌است.[65] با این حال نویسندگان جدیدتر مانند نیکوس سالینگاروس، در این ادعاها شک دارند.[66] آزمایش‌های جورج مارکوفسکی، دانشمند کامپیوتر، نتوانست هیچ ساماندهی برای مستطیل طلایی پیدا کند.[67]

معماری اسلامی
اطلاعات بیشتر: معماری اسلامی
مسجد سلیمیه، ۱۵۶۹–۱۵۷۵

آنتونیو فرناندز-پورتاس، مورخ هنر اسلامی، مطرح کرده که الحمرا، مانند مسجد-کلیسای جامع قرطبه،[68] با استفاده از واحد فوت مسلمان اندلس که حدود ۰/۶۲ متر (۲ فوت) است، طراحی شده‌است. در حیاط شیران کاخ، نسبت‌ها دنباله ای از ریشه اعداد را دنبال می‌کند. یک مستطیل با اضلاع ۱ و ۲√ (با قضیه فیثاغورس) و قطر ۳√، که مثلث قائم الزاویه ساخته شده توسط اضلاع حیاط را توصیف می‌کند. این مجموعه با ۴√ (نسبت ۱:۲)، ۵√ و غیره ادامه می‌یابد. الگوهای تزئینی نیز تناسبات مشابه‌ای دارند. ۲√ مربع‌هایی درون دایره‌ها و ستاره هشت پر ایجاد می‌کند و ۳√ ستاره شش پر ایجاد می‌کند. هیچ مدرکی برای اثبات ادعاهای قبلی مبنی بر استفاده از نسبت طلایی در الحمرا وجود ندارد.[10][69] حیاط شیران بین تالار دو خواهر و تالار آبنسراجس قرار دارد. از مراکز این دو سالن و چهار گوشه داخلی بارگاه شیرها می‌توان یک شش ضلعی منتظم رسم کرد.[70]

مسجد سلیمیه در ادرنه، ترکیه توسط معمار سنان ساخته شد تا فضایی فراهم کند که محراب از هر نقطه داخل ساختمان دیده شود. بر این اساس فضای مرکزی بسیار بزرگ به صورت هشت ضلعی ساماندهی شده‌است، که توسط هشت ستون عظیم تشکیل شده و دارای یک گنبد مدور با قطر ۳۱٫۲۵ متر (۱۰۲٫۵ فوت) و ارتفاع ۴۳ متر (۱۴۱ فوت) است. هشت ضلعی در داخل با چهار نیم گنبد و در خارج بنا با چهار مناره فوق‌العاده بلند ۸۳ متری (۲۷۲ فوت) به صورت مربع درآمده است؛ بنابراین نقشه ساختمان یک دایره درون یک هشت ضلعی درون یک مربع است.[71]

معماری مغولی
نوشتار‌های اصلی: معماری گورکانی و فاتح پور سیکری
آرامگاه تاج محل با بخشی از باغ‌های مجموعه در آگره.

معماری مغولی، همان‌طور که در شهر متروکه شاهنشاهی فاتح پور سیکری و مجموعه تاج محل دیده می‌شود، دارای نظم ریاضی متمایز و زیبایی مبتنی بر تقارن و هماهنگی است.[11][72]

تاج محل نمونه معماری مغولی است و پردیس[73] و قدرت امپراتور مغول شاه جهان را با مقیاس، تقارن و دکوراسیون پرهزینه‌اش نمایش می‌دهد. آرامگاه مرمر سفید که با پرچین‌کاری تزئین شده، دروازه بزرگ (Darwaza-i rauza)، ساختمانهای دیگر، باغها و مسیرها با هم یک طرح سلسله مراتبی یکپارچه را تشکیل می‌دهند. این ساختمان‌ها شامل یک مسجد ساخته شده با سنگ ماسه قرمز در غرب، و یک ساختمان تقریباً یکسان دیگر به نام جواب در سمت شرق برای حفظ تقارن دو طرفه مجموعه است. چهارباغ از چهار بخش تشکیل شده‌است که نماد چهار رودخانه پردیس است و نمای آرامگاه را بازتاب می‌دهد. اینها به نوبه خود به ۱۶ قسمت تقسیم می‌شوند.[74]

پلان سایت مجموعه تاج محل. دروازه بزرگ در سمت راست، آرامگاه در مرکز آن قرار دارد بین مسجد (پایین) و جواب قرار گرفته‌است. این پلان شامل اشکال مربعی و هشت ضلعی است.

مجموعه تاج محل بر روی شبکه ای بنا شده که خود به شبکه‌های کوچکتر تقسیم می‌شود. کوچ و بارو، مورخان معماری، با گزارش‌های سنتی دربارهٔ ابعاد مجموعه موافق هستند. طبق این گزارش‌ها عرض مجموعه ۳۷۴ یارد مغولی یا گز است[persian-alpha 2] و مساحت محوطه اصلی آن سه ۳۷۴ گز مربع است. اینها در فضاهایی مانند بازار و کاروانسرا به مدولهای ۱۷ گزی تقسیم شده‌اند. مدول باغ و تراسها ۲۳ گز و عرض آن‌ها ۳۶۸ گز (۱۶ × ۲۳) است. آرامگاه، مسجد و مهمانسرا روی یک شبکه ۷ گزی گذاشته شده‌است به باور کوچ و بارو اگر اضلاع هشت ضلعی که به‌طور مکرر در مجموعه استفاده شده ۷ واحدی باشند، می‌توان نتیجه گرفت که عرض آن ۱۷ واحد است، که به توضیح انتخاب نسبت‌ها در مجموعه کمک کند.[75]

معماری مسیحی

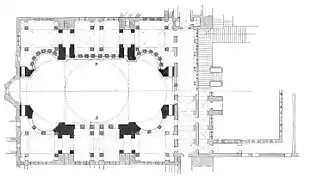
بازیلیکای مسیحی ایاصوفیه از دوره ایلخانی در بیزانتیوم (استانبول کنونی) که برای اولین بار در سال ۵۳۷ ساخته شد (و دو بار بازسازی شد)، به مدت هزار سال بزرگترین کلیسای جامع جهان بود. این ساختمان الهام بخش بسیاری از بناهای بعدی از جمله مسجد سلطان احمد و دیگر مساجد شهر بود. معماری بیزانسی شامل یک شبستان است که با یک گنبد مدور و دو نیم گنبد مسقف می‌شود، قطر همگی (۳۱ متر (۱۰۲ فوت)) است و پنج نیم گنبد کوچکتر دیگر یک محراب و چهار گوشه گرد برای شبستان مستطیل شکل تشکیل می‌دهند.[76] معماران قرون وسطایی معماری بیزانسی را اینگونه تفسیر کردند که چهارگوش در پایین نشان دهنده دنیا و گنبد در بالا نشاندهنده آسمانهای الهی است.[77] امپراتور ژوستینین یکم دو هندسه دان به نام‌های ایزیدور مایلتوس و آنتمیوس ترالس را به عنوان معمار این بنا استخدام کرد. ایزیدور آثار ارشمیدس را در زمینه هندسه فضایی گردآوری کرد و تحت تأثیر او قرار داشت.[12][78]

پلان ایا صوفیه

اهمیت غسل تعمید در مسیحیت در مقیاس معماری تعمیدگاه‌ها منعکس شده‌است. قدیمی‌ترین تعمیدگاه، تعمیدگاه لاتران در رم است که در سال ۴۴۰ ساخته شده،[79] هندسه این ساختمان هشت‌ضلعی است و ساخت تعمیدگاه‌های هشت ضلعی پس از آن باب شد. حوضچه تعمید در داخل این ساختمانها اغلب هشت ضلعی بود، اگرچه بزرگترین تعمیدگاه ایتالیا در پیزا که بین سالهای ۱۱۵۲ تا ۱۳۶۳ ساخته شده، مدور است و دارای یک حوضچه تعمید هشت ضلعی است. ارتفاع این تعمیدگاه ۵۴٫۸۶ متر (۱۸۰٫۰ فوت) و قطر آن ۳۴٫۱۳ متر (۱۱۲٫۰ فوت) (نسبت ۸:۵) است.[80] سنت امبروس می‌نویسد که حوضچه‌ها و تعمیدگاه‌ها هشت ضلعی هستند «زیرا در روز هشتم، با برخاستن، مسیح اسارت مرگ را سست کرده و مردگان را از گورهای خود دریافت می‌کند.»[81][82] سنت آگوستین به همین ترتیب روز هشتم را اینگونه توصیف می‌کند «جاویدان … مقدس شده با رستاخیز مسیح».[82][83] تعمیدگاه هشت ضلعی سنت جان در فلورانس بین سالهای ۱۰۵۹ و ۱۱۲۸ ساخته شده و یکی از قدیمی‌ترین بناها در آن شهر است و یکی از آخرین ساختمانهای سنتی دوران باستان کلاسیک به‌شمار می‌رود. این ساختمان در رنسانس شهر فلورانس بسیار تأثیرگذار بود، زیرا معماران بزرگی از جمله فرانچسکو تالنتی، آلبرتی و برونلسکی از آن به عنوان الگوی معماری کلاسیک استفاده کردند.[84]

  • طاق‌نمای شبستان ایا صوفیه، استانبول، ۵۶۲
  • تعمیدگاه هشت‌ضلعی سنت جان، فلورانس، در سال ۱۱۲۸ کامل شد
  • تقارن‌های پنج‌گانه در کلیسای سنت جان نپوموک در زلنا هورا، ۱۷۲۱
  • نمای ساگرادا فامیلیا اثر آنتونی گائودی، بارسلونا، ۱۸۸۲
  • کلیسای جامع برازیلیا اثر اسکار نیمایر، ۱۹۷۰
  • کلیسای جامع مریم مقدس، سانفرانسیسکو، ۱۹۷۱
  • ستون مرکزی کلیسای مدور استرلارس در برنهلم، دانمارک

تزئینات ریاضیاتی

تزئینات معماری اسلامی

ساختمان‌های اسلامی اغلب با الگوهای هندسی تزئین می‌شوند. این الگوها معمولاً با کاشی‌کاری یا مفروش‌سازی (پرکردن یا فرش کردن یک صفحه با مجموعه‌ای از اشکال هندسی) ریاضی تشکیل شده‌اند و جنس کاشی‌ها از سرامیک (گره، زلیج) است.[12] از تقارن‌هایی مانند ستاره‌های دارای شش نفطه، هشت یا مضربی از هشت نقطه در الگوهای اسلامی استفاده شده‌است. برخی از این الگوها بر اساس نقوش خاتم سلیمان ساخته شده‌اند، که یک ستاره هشت پر است و از دو مربع ساخته شده‌است، از این دو مربع هم مرکز یکی ۴۵ درجه نسبت به دیگری چرخیده‌است.[85] الگوهای اسلامی از بیشتر ۱۷ گروه سطح کریستالوگرافیک بهره می‌برند. در اوایل سال ۱۹۴۴ ادیت مولر نشان داد که در تزئینات الحمرا از ۱۱ گروه سطح کریستالوگرافیک استفاده شده‌است، در حالی که در سال ۱۹۸۶ برانکو گرونباوم ادعا کرد که ۱۳ گروه سطح کریستالوگرافیک را در الحمرا پیدا کرده‌است، و با اختلاف نظر اظهار داشت که چهار گروه باقی مانده در هیچ‌کدام از تزئینات اسلامی یافت نمی‌شوند.[85]

تزئینات معماری مدرن

در اواخر قرن ۲۰ میلادی، مفاهیم جدید ریاضی مانند هندسه فراکتال و کاشی کاری‌های غیر دوره ای برای فراهم کردن پوشش‌های جذاب و زیبا برای ساختمان‌ها توسط معماران به گار گرفته شدند.[4] در سال ۱۹۱۳، آدولف لوس، معمار مدرنیست اعلام کرد که «تزیینات جرم است»،[86] و بر تفکر معماری در قرن بیستم تأثیر گذاشت. معماران در قرن ۲۱، دوباره شروع به کاوش در مورد استفاده از تزیینات کردند. تزئینات قرن بیست و یکمی بسیار متنوع است. مرکز همایش و تالار کنسرت هارپا اثر هنینگ لارسن، در شهر ریکیاویک دارای چیزی است که به نظر می‌رسد یک دیوار کریستالی از سنگ ساخته شده از بلوک‌های بزرگ شیشه است.[86] دانشگاه راونزبورن در لندن با ۲۸۰۰۰ کاشی با روکش آلومینیومی در رنگ‌ها قرمز، سفید و قهوه‌ای تزئین شده‌است و پنجره‌های دایره ای شکل در ابعاد گوناگون را بهم وصل می‌کنند. در نمای این ساختمان از سه نوع شکل استفاده شده‌است یک مثلث متساوی الاضلاع و دو پنج‌ضلعی نامنظم.[87][88][88] کتابخانه کانازاوا یومیمیرای اثر کازومی کودو یک شبکه تزئینی ساخته شده از بلوک‌های دایره ای شکل کوچک شیشه‌ای درون دیوارهای بتونی ساده ایجاد کرده‌است.[86]

  • کالج راونزبورن، لندن، ۲۰۱۰
  • مرکز کنسرت و کنفرانس هارپا، ایسلند، ۲۰۱۱
  • کتابخانه کانازاوا یومیمیرای، ژاپن، ۲۰۱۱
  • موزه سمیه، مکزیک، ۲۰۱۱

استحکامات

اروپا

معماری استحکامات از قلعه‌های قرون وسطایی که دارای دیوارهای سنگی بلند یا گاه کم ارتفاع بودند و قلعه‌های متقارن ستاره‌ای شکل در اواسط قرن پانزدهم تا نوزدهم که می‌توانستند در برابر بمباران توپخانه مقاومت کنند، تکامل یافت. هندسه اشکال ستاره‌ای برای پرهیز از مناطق مرده‌ای که پیاده‌نظام مهاجم به واسطه آن می‌تواند از آتش مدافعان قلعه پناه بگیرد، به کار گرفته شد. طرفین نقاط بیرون زده زاویه دار بودند تا زمین در تیررس مدافعان قرار گیرد و آتش متقابل (از هر دو طرف) را آنسوی هر نقطه بیرون زده ایجاد کند. از معماران مشهوری که چنین استحکاماتی را طراحی کرده‌اند می‌توان به میکل‌آنژ، بالداساره پروتزی، وینچنزو اسکاموزی و سباستین لو پرتر دو ووبن اشاره کرد.[89][90]

زیگفرید گیدیون مورخ معماری استدلال می‌کند که استحکامات ستاره ای شکل تأثیری شگرف بر الگوسازی شهر ایده‌آل رنسانس داشته‌است: «رنسانس توسط یک نوع شهر هیپنوتیزم شد که برای یک قرن و نیم - از فیلارته تا اسکاموزی - همه طرح‌های آرمان شهری را تحت تأثیر خود قرار داده بود: آن شهر ستاره‌ای شکل است.»[91]

چین
یک تولو در یانگدینگ، فوجیان

در معماری چینی، تولوهای استان فوجیان سازه‌های دفاعی دایره ای شکل و معمول با دیوارهای اغلب خالی و یک در چوبی با روکش آهن است که قدمت برخی آنها به قرن شانزدهم برمی گردد. بالای دیوارها سقف‌هایی قرار دارند که به آرامی هم به سمت خارج و هم به سمت داخل شیب دارند و حلقه ای را تشکیل می‌دهند. در مرکز دایره یک حیاط سنگفرش باز قرار دارد که غالباً دارای یک چاه است و توسط گذرگاهی چوبی که ارتفاع آن تا پنج طبقه هم می‌رسد، احاطه شده‌است.[92]

اهداف زیست‌محیطی
یخدانی در یزد

معماران ممکن است فرم ساختمان را برای دستیابی به اهداف زیست‌محیطی برگزینند.[93] به عنوان مثال، تبر سنت ماری ۳۰ در لندن یک جسم دوّار است که با استفاده از مدل‌سازی پارامتریک طراحی شده‌است. هندسه آن صرفاً به دلایل زیبایی شناختی انتخاب نشده، بلکه به حداقل رساندن جریان‌های هوای گردان در پایه آن نیز مدنظر بوده‌است. علیرغم سطح ظاهراً منحنی ساختمان، تمام صفحات شیشه ای که پوست آن را تشکیل می‌دهند، تخت هستند، به جز عدسی در بالای آن. بیشتر صفحات چهارضلعی هستند، زیرا می‌توان آنها را از شیشه مستطیلی با اتلاف کمتر مواد نسبت به صفحه‌های مثلثی برش داد.[94]

یخچال‌های سنتی (یخدان) ایرانی به عنوان یک کولر تبخیری عمل می‌کند. در بالای سطح زمین ساختاری گنبدی شکل دارد و فضای ذخیره‌سازی زیرزمینی برای یخ و گاهی اوقات غذا نیز دارد. فضای زیرزمینی و ساختار ضخیم مقاوم در برابر حرارت، فضای ذخیره‌سازی را در طول سال عایق بندی می‌کند. فضای داخلی اغلب با بادگیر خنک می‌شد. از یخ در تابستان برای تهیه فالوده استفاده می‌کردند.[95]

جستارهای وابسته

پانویس
  1. یک فوت رومی حدوداً ۰٫۲۹۶ متر (۰٫۹۷ فوت) بود.
  2. ۱ گز حدوداً ۰٫۸۶ متر (۲٫۸ فوت) است.

منابع
  1. Freiberger, Marianne (1 March 2007). "Perfect buildings: the maths of modern architecture". Plus magazine. Retrieved 5 October 2015.
  2. Rian, Iasef Md; Park, Jin-Ho; Ahn, Hyung Uk; Chang, Dongkuk (2007). "Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho". Building and Environment. 42 (12): 4093–4107. doi:10.1016/j.buildenv.2007.01.028.
  3. Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s. Birkhäuser. pp. chapter 1. 1–24. ISBN 978-3-319-00136-4.
  4. Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future. Birkhäuser. pp. chapter 48. 1–24. ISBN 978-3-319-00142-5.
  5. "Architectural Engineering Overview" (PDF). Sloan Career Cornerstone Center. Archived from the original (PDF) on 14 July 2015. Retrieved 11 October 2015.
  6. Leyton, Michael (2001). A Generative Theory of Shape. Springer. ISBN 978-3-540-42717-9.
  7. Stakhov, Alexey; Olsen, Olsen (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. ISBN 978-981-277-582-5.
  8. Smith, William (1870). Dictionary of Greek and Roman Biography and Mythology. Little, Brown. p. 620.
  9. Vitruvius (2009). On Architecture. Penguin Books. pp. 8–9. ISBN 978-0-14-193195-1.
  10. Tennant, Raymond (July 2003). "International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen" (PDF). International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science.
  11. Rai, Jaswant (1993). "Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri". Journal of King Saud University, Architecture & Planning. 5 (1): 19–48.
  12. O'Connor, J. J.; Robertson, E. F. (February 2002). "Mathematics and Architecture". University of St Andrews. Retrieved 4 October 2015.
  13. van den Hoeven, Saskia; van der Veen, Maartje (2010). "Muqarnas: Mathematics in Islamic Arts" (PDF). Utrecht University. Archived from the original (PDF) on 4 March 2016. Retrieved 30 September 2015.
  14. Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 103–106. ISBN 978-0-521-72876-8.
  15. Williams, Kim; Ostwald, Michael J. (9 February 2015). Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. pp. 42, 48. ISBN 978-3-319-00137-1.
  16. Roth, Leland M. (1992). Understanding Architecture: Its Elements, History, And Meaning. Boulder: Westview Press. p. 36. ISBN 0-06-438493-4.
  17. Claridge, Amanda (1998). Rome. Oxford Archaeological Guides. Oxford Oxfordshire: Oxford University Press. pp. 204–5. ISBN 0-19-288003-9.
  18. Lancaster, Lynne C. (2005). Concrete Vaulted Construction in Imperial Rome: Innovations in Context. Cambridge: Cambridge University Press. pp. 44–46. ISBN 0-521-84202-6.
  19. March, Lionel (1996). "Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria". Architectural Research Quarterly. 2 (1): 54–65. doi:10.1017/S135913550000110X.
  20. "Sphere circumscribing a cube". Mathalino.com Engineering Math Review. Retrieved 4 October 2015.
  21. Typ 525.69.781, Houghton Library, Harvard University
  22. Andersen, Kirsti (2008). The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. Springer. pp. 117–121. ISBN 978-0-387-48946-9.
  23. Ruhl, Carsten (7 April 2011). "Palladianism: From the Italian Villa to International Architecture". European History Online. Retrieved 3 October 2015.
  24. Copplestone, Trewin (1963). World Architecture. Hamlyn. p. 251.
  25. Wassell, Stephen R. "The Mathematics Of Palladio's Villas: Workshop '98". Nexus Network Journal. Retrieved 3 October 2015.
  26. Palladio, Andrea; Tavernor, Robert; Schofield, Richard (trans.) (1997) [1570]. I quattro libri dell'architettura. MIT Press. p. book I, chapter xxi, page 57.
  27. Scamozzi, Vincenzo; Vroom, W. H. M. (trans.) (2003) [1615]. The Idea of a Universal Architecture. Architectura & Natura.
  28. Borys, Ann Marie (28 March 2014). Vincenzo Scamozzi and the Chorography of Early Modern Architecture. Ashgate Publishing. pp. 140–148 and passim. ISBN 978-1-4094-5580-6.
  29. Beckh, Matthias (2015). Hyperbolic Structures: Shukhov's Lattice Towers – Forerunners of Modern Lightweight Construction. John Wiley & Sons. pp. 75 and passim. ISBN 978-1-118-93268-1.
  30. "The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span". The Engineer: 292–294. 19 March 1897.
  31. Graefe, Rainer; et al. (1990). -3421029849 Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion Check |url= value (help). Deutsche Verlags-Anstalt. pp. -3421029849/page/n110 110–114. ISBN 3-421-02984-9.
  32. Hatherley, Owen (4 November 2011). "The Constructivists and the Russian Revolution in Art and Architecture". The Guardian. Retrieved 6 June 2016.
  33. "Rietveld Schröderhuis (Rietveld Schröder House)". World Heritage Centre. UNESCO. Retrieved 13 December 2012.
  34. English Heritage, "Details from listed building database (1358981)", [[National Heritage List for England]]. Unknown parameter |separator= ignored (help); URL–wikilink conflict (help)
  35. Moholy-Nagy, Laszlo; Hoffman, Daphne M. (trans.) (1938). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. New Bauhaus Books. p. 46.
  36. Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 306. ISBN 978-0-691-16528-8.
  37. Le Corbusier (2004) [1954 and 1958]. The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. Birkhäuser. ISBN 3-7643-6188-3.
  38. Hanser, David A. (2006). Architecture of France. Greenwood Publishing Group. p. 211. ISBN 978-0-313-31902-0.
  39. Salingaros, Nikos. "Architecture, Patterns, and Mathematics". Nexus Network Journal. Retrieved 9 October 2015. Updated version of Salingaros, Nikos (April 1999). "Architecture, Patterns, and Mathematics". Nexus Network Journal. 1 (2): 75–86. doi:10.1007/s00004-998-0006-0. S2CID 120544101.
  40. "Vanity Fair's World Architecture Survey: the Complete Results". Vanity Fair. 30 June 2010. Retrieved 22 July 2010.
  41. "Biosphere". A view on cities. Archived from the original on 27 September 2007. Retrieved 1 October 2015.
  42. "Denver International Airport Press Kit" (PDF). Denver International Airport. 2014. Archived from the original (PDF) on 12 April 2015. Retrieved 5 October 2015.
  43. "Denver International Airport". Fenstress Architects. Retrieved 5 October 2015.
  44. Hahn, Alexander J. (4 February 2013). "Mathematical Excursions To Architecture". Inside Science. Retrieved 5 October 2015.
  45. Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 139–141. ISBN 978-3-937954-07-3.
  46. Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 124–125. ISBN 978-3-937954-07-3.
  47. Gehry, Frank O.; Mudford, Grant; Koshalek, Richard (2009). Symphony: Frank Gehry's Walt Disney Concert Hall. Five Ties. ISBN 978-0-9794727-4-9.
  48. Garcetti, Gil (2004). Iron: Erecting the Walt Disney Concert Hall. Princeton Architectural Press. ISBN 978-1-890449-28-5.
  49. Bartlett, Christopher (2014). "The Design of The Great Pyramid of Khufu". Nexus Network Journal. 16 (2): 299–311. doi:10.1007/s00004-014-0193-9.
  50. Markowsky, George (January 1992). "Misconceptions About the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1): 2–19. doi:10.1080/07468342.1992.11973428. Archived from the original (PDF) on 2008-04-08. Retrieved 2015-10-01.
  51. Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. p. 61. ISBN 0-7679-0816-3.
  52. Gazalé, Midhat (1999). Gnomon: From Pharaohs to Fractals. Princeton University Press.
  53. Cooke, Roger L. (2011). The History of Mathematics: A Brief Course (2nd ed.). John Wiley & Sons. pp. 237–238. ISBN 978-1-118-03024-0.
  54. Gillings, Richard J. (1982). Mathematics in the Time of the Pharaohs. Dover. p. 161.
  55. Kramrisch, Stella (1976), The Hindu Temple Volume 1 & 2, شابک ‎۸۱−۲۰۸−۰۲۲۳−۳
  56. Vibhuti Sachdev, Giles Tillotson (2004). Building Jaipur: The Making of an Indian City. pp. 155–160. ISBN 978-1-86189-137-2.
  57. Ifrah, Georges (1998). A Universal History of Numbers. Penguin.
  58. "Fractals in Indian Architecture". Yale University. Archived from the original on 6 February 2012. Retrieved 1 October 2015.
  59. King, Anthony D. (2005). Buildings and Society: Essays on the Social Development of the Built Environment. Taylor & Francis. p. 72. ISBN 0-203-48075-9.
  60. Maor, Eli (2007). The Pythagorean Theorem: A 4,000-year History. Princeton University Press. p. 19. ISBN 978-0-691-12526-8.
  61. Norwich, John Julius (2001). Great Architecture of the World. Artists House. p. 63.
  62. Penrose, Francis (1973) [1851]. Principles of Athenian Architecture. Society of Dilettanti. p. ch. II.3, plate 9.
  63. Stevens, Gorham P. (July 1962). "Concerning the Impressiveness of the Parthenon". American Journal of Archaeology. 66 (3): 337–338. doi:10.2307/501468. JSTOR 501468.
  64. Euclid. Elements. Book 6, Proposition 30.
  65. Archibald, R. C. "Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series". Retrieved 1 October 2015.
  66. Applications of the Golden Mean to Architecture
  67. Markowsky, George (January 1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1): 2–19. doi:10.1080/07468342.1992.11973428. Archived from the original (PDF) on 2008-04-08. Retrieved 2015-10-01.
  68. Gedal, Najib. "The Great Mosque of Cordoba: Geometric Analysis". Islamic Art & Architecture. Archived from the original on 2 October 2015. Retrieved 16 October 2015.
  69. Irwin, Robert (26 May 2011). The Alhambra. Profile Books. pp. 109–112. ISBN 978-1-84765-098-6.
  70. Robertson, Ann (2007). "Revisiting the Geometry of the Sala de Dos Hermanas" (PDF). BRIDGES. Retrieved 11 October 2015.
  71. Blair, Sheila; Bloom, Jonathan M. (1995). The Art and Architecture of Islam 1250–1800. Yale University Press. ISBN 0-300-06465-9.
  72. Michell, George; Pasricha, Amit (2011). Mughal Architecture & Gardens. Antique Collectors Club. ISBN 978-1-85149-670-9.
  73. Parker, Philip (2010). World History. Dorling Kindersley. p. 224. ISBN 978-1-4053-4124-0.
  74. Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st ed.). Thames & Hudson. pp. 24 and passim. ISBN 0-500-34209-1.
  75. Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st ed.). Thames & Hudson. pp. 104–109. ISBN 0-500-34209-1.
  76. Fazio, Michael; Moffett, Marian; Wodehouse, Lawrence (2009). Buildings Across Time (3rd ed.). McGraw-Hill Higher Education. ISBN 978-0-07-305304-2.
  77. Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 48. ISBN 978-0-691-16528-8.
  78. Kleiner, Fred S.; Mamiya, Christin J. (2008). Gardner's Art Through the Ages: Volume I, Chapters 1–18 (12th ed.). Wadsworth. p. 329. ISBN 978-0-495-46740-3.
  79. Menander, Hanna; Brandt, Olof; Appetechia, Agostina; Thorén, Håkan (2010). "The Lateran Baptistery in Three Dimensions" (PDF). Swedish National Heritage Board. Retrieved 30 October 2015.
  80. "The Baptistery". The Leaning Tower of Pisa. Retrieved 30 October 2015.
  81. Huyser-Konig, Joan. "Theological Reasons for Baptistry Shapes". Calvin Institute of Christian Worship. Retrieved 30 October 2015.
  82. Kuehn, Regina (1992). A Place for Baptism. Liturgy Training Publications. pp. 53–60. ISBN 978-0-929650-00-5.
  83. Augustine of Hippo (426). The City of God. p. Book 22, Chapter 30.
  84. Kleiner, Fred (2012). Gardner's Art through the Ages: A Global History. Cengage Learning. pp. 355–356. ISBN 978-1-133-71116-2.
  85. Rønning, Frode. "Islamic Patterns And Symmetry Groups" (PDF). University of Exeter. Retrieved 18 April 2014.
  86. Gibberd, Matt; Hill, Albert (20 August 2013). "The Return of Ornamentation". The Telegraph. Retrieved 12 October 2015.
  87. "Ravensbourne College by Foreign Office Architects". de zeen magazine. 13 September 2010. Retrieved 12 October 2015.
  88. Bizley, Graham. "FOA's peninsula patterns for Ravensbourne College". bdonline.co.uk. Retrieved 16 October 2015.
  89. Duffy, C. (1975). Fire & Stone, The Science of Fortress Warfare 1660–1860. Booksales. ISBN 978-0-7858-2109-0.
  90. Chandler, David (1990). The Art of Warfare in the Age of Marlborough. Spellmount. ISBN 978-0-946771-42-4.
  91. Giedion, Siegfried (1962) [1941]. Space, Time and Architecture. Harvard University Press. p. 43.
  92. O'Neill, Tom (4 January 2015). "China's Remote Fortresses Lose Residents, Gain Tourists". National Geographic. Retrieved 6 January 2017.
  93. Simitch, Andrea; Warke, Val (2014). The Language of Architecture: 26 Principles Every Architect Should Know. Rockport Publishers. p. 191. ISBN 978-1-62788-048-0.
  94. Freiberger, Marianne (1 March 2007). "Perfect buildings: the maths of modern architecture". Plus magazine. Retrieved 5 October 2015.
  95. Mahdavinejad, M.; Javanrudi, Kavan (July 2012). "Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates". Asian Culture and History. 4 (2). doi:10.5539/ach.v4n2p133.

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.