مکتب فیثاغوری
مکتب فیثاغوری یا پیتاگوریگرایی (به انگلیسی: Pythagoreanism) یکی از مکاتب فلسفی پیشاسقراطی بود که توسط فیثاغورس بنیان نهاده شد.

فیثاغورس از شاگردانش انجمنی در شهر کُرُتُن در جنوب ایتالیا تشکیل داد. او در آنجا نه تنها به آموزش ریاضیات میپرداخت؛ بلکه از ریاضیات نتایج فلسفی و عرفانی میگرفت.[1]
باید دانست که پیروان فیثاغورس، تمام نظریاتشان را به «استاد» نسبت میدادند؛ بنابراین، مشخص نیست که چه اندازه از آیین فیثاغوری از خود فیثاغورس، و چه اندازهٔ آن از شاگردانش است.[1]
نظریات فیثاغوریان
ابداع ریاضیات

فیثاغورس عموماً به عنوان کاشف قضیه فیثاغورس شناخته میشود، اما نقش او در ریاضیات بسی ژرفتر و برجسته تر است.
البته ریاضیات بسیار پیش تر از فیثاغورس نیز وجود داشته و زمان واحدی را نمیتوان به عنوان آغاز ریاضی ذکر کرد؛ و نقش فیثاغورس تبیین اصول ریاضیات بود.
امروزه حتی تصور این موضوع که ریاضیات بدون استدلال چه وضع و حالی داشتهاست، دشوار است؛ اما باید دانست که قبل از فیثاغورس هیچکس نظر روشنی دربارهٔ این موضوع نداشت که استدلال باید مبنی بر مفروضات باشد. به عبارتی استدلال، مسئلهٔ تعریف شدهای نبود.
در واقع میتوان گفت بنا به قول مشهور، فیثاغورس نخستین کسی بود که روی این نکته اصرار ورزید که در هندسه باید ابتدا مفروضات را تعیین کرد و سپس از آنها نتیجه گرفت.
مفروضات نیز عبارت بودند:
- «اصول موضوع»: حقایق بدیهی، خودبه خود لازم و بدون تعریف؛
- «اصول متعارفی»: حقایق تعریفی و قراردادی، حقایقی که با استفاده از اصول موضوع تعریف میشوند؛
- «قضایای از پیش اثبات شده»: هر قضیهای که با استفاده از اصول موضوع و اصول متعارفی اثبات شود، خودش میتواند به عنوان یکی از مفروضات در استدلالهای دیگر استفاده بشود.
اینکه فیثاغورس استدلال را وارد ریاضیات کرد، از مهمترین حوادث علمی است و از این رو فیثاغورس را ابداعگر ریاضیات خواندهاند.[1]
قبل از فیثاغورس، هندسه عبارت بود از مجموعهٔ قواعدی که ماحصل تجارب و ادراکات متفرق بودهاند؛ تجارب و قواعدی که هیچگونه ارتباطی با هم نداشتند؛ اما فیثاغورس از یک پایه جلو رفت و همچون یک زنجیره، قضایا را یکی پس از دیگری با استفاده از قضایای قبلی اثبات کرد؛ بنابراین مجموعهٔ قواعد متفرقه ریاضی را از تعداد بسیار کمی اصول نتیجه گرفت.
آنها همچنین مقدمههای نظریهٔ اعداد را پی ریزی کردند و تصاعدهای حسابی و هندسی را کشف نمودند.
فیثاغورس میگفت که او حساب را والاتر از نیازهای بازرگانی میداند. به همین سبب در مکتب فیثاغوری، حتی شمار عملی هم مورد توجه قرار نگرفت. آنها تنها دربارهٔ ویژگیهای عددها کار میکردند. در ضمن، ویژگی عدد را هم به یاری ساختمانهای هندسی پیدا میکردند. با وجود این، رواج نوعی دستگاه مناسب برای عددنویسی را در یونان، به فیثاغوریان یا هواداران نزدیک آنها نسبت میدهند.
در این نوع عددنویسی که از فینیقیها گرفته بودند، از حرفهای الفبای فینیقی، برای نوشتن عددها استفاده شد: ۹ حرف اول الفبا برای عددهای از ۱ تا ۹، ۹ حرف بعدی برای نشان دادن دهگان (۲۰، ۱۰،... ، ۹۰) و ۹ حرف بعدی برای صدها (۲۰۰، ۱۰۰،... ، ۹۰۰). برای حرف از عدد تشخیص داده شود، بالای عدد خط کوتاهی میگذاشتند. برای نشان دادن عددهای بزرگتر از نشانههای اضافی استفاده میکردند. وقتی نشانهای شبیه ویرگول را جلو عددی میگذاشتند، به معنای هزار برابر آن بود، برای ده هزار برابر عدد، یک نقطه جلو عدد میگذاشتند.
استنتاج خردگرایی فلسفی از ریاضیات
فیثاغورس پایهگذار خردگرایی در معنای فلسفی واژه است. خردگرایی فلسفی به این معناست که میتوان با روش تفکر محض به حقیقت فلسفی رسید.[1]
این که ۲ + ۲ میشود ۴، نوعی دانش دقیق است که منتج از مشاهده نیست، بلکه نتیجهای «تحلیلی» است که از تعریف ۲ ناشی شدهاست. اگر به این نکتهٔ دقیق توجه کنیم که ۲- با هیچ چیز مشاهدهپذیری متناظر نیست، صدق اصل تحلیلی بودن ریاضی آشکارتر میشود. فیثاغورس بدین ترتیب نتیجه گرفت که میتوان با تفکر محض به حقایقی دست یافت؛ یعنی خردگرایی فلسفی را نتیجه گرفت.[1]
راه تفکر محض از راه مشاهده و آزمایش جداست و چون حقایق ریاضی قطعی هستند، برتر از واقعیتهایی هستند که از مشاهده نتیجه شدهاند.[1]
اما در عین حال به نظر میرسید که ریاضیات علم به چیزهایی است که «تصوری» یا ذهنی اند، و در اندیشهٔ ما هستند؛ اما در جهان خارج نیستند.[1]
پس فیثاغورس عقیده به وجود جهانی کاملاً فراحسی، یعنی جهان چیزهای «مثالی» را رواج داد؛ جهانی که ناخالصی و آلودگی دنیای خاکی را ندارد، و تنها راه کسب معرفت نسبت به آن تفکر محض است. معرفتی که از این راه حاصل آید، یقینی است.[1]
باور به جهان اشیاء «مثالی»، اثرات عمیقی بر افلاطون گذاشت و هستهٔ مرکزی افکار او شد، و بعدها این آرا توسط فیلسوفان مسلمان گسترش یافت.
عدد، اساس عالم
فیثاغورس کشفهای مهمی در ریاضیات کرد که او را هرچه بیشتر به استنتاج عرفانی از ریاضیات، سوق داد.
یکی از این کشفها در زمینهٔ موسیقی بود. فیثاغورس و یکی از شاگردانش به نام فیلولائوس کشف کردند که مبنای گام موسیقی بر اعداد است، یعنی میتوان فاصلههای هارمونیک را با نسبتهای عددی توضیح داد.[1] برای مثال متوجه شد که آهنگ موزون روی صدای سه سیم، زمانی به دست میآید که طول این سیمها، متناسب با عددهای ۳ و ۴ و ۶ باشد. فیثاغوریان این بستگی عدد را در پدیدههای دیگر نیز پیدا کردند. از جمله، نسبت تعداد وجهها، راسها و یالهای مکعب هم برابر است با نسبت عددی ۶:۸:۱۲.
همچنین فیثاغوریان متوجه شدند که اگر بخواهیم صفحهای را با یک نوع چندضلعی منتظم بپوشانیم، فقط سه حالت وجود دارد؛ دور و بر یک نقطه از صفحه را میتوان با ۶ مثلث متساویالاضلاع، با ۴ مربع، یا با ۳ ششضلعی منتظم پر کرد، بهطوریکه دور و بر نقطه را بهطور کامل بپوشاند. همانطور که مشاهده میشود، تعداد این چندضلعیها با همان نسبت ۳:۴:۶ مطابقت دارد و اگر نسبت تعداد اضلاع این چندضلعیها را در نظر بگیریم، به همان نسبت ۳:۴:۶ میرسیم.
یاران و شاگردان فیثاغورس این مشاهدهها را تعمیم دادند و گفتند اساس عالم عدد است.[1] به باور آنان عدد، علت هماهنگی و نظم در طبیعت است؛ رابطههای ذاتی جهان ما، حکومت و دوام جاودانی آن را تضمین میکند. عدد، قانون طبیعت است، بر خدایان و بر مرگ حکومت میکند و شرط هرگونه شناخت و دانشی است.
تمام اشیاء، تقلید و نمونهای از عدد هستند. عددهای ساده را چون شکلهایی سازندهٔ اشیاء میپنداشتند، مانند نقشهای روی تاس نرد، و پدیدهها را ترکیبهای مکانمند میدانستند.[1]
بنابراین شعار مدرسه فیثاغورسی نیز «همه چیز اعداد است» قرار گرفت.[2]
پیروان مکتب فیثاغوری اعتقاد داشتند که همهٔ پدیدههای گیتی از بستگیهای عددی مشخصی پیروی میکنند و یک هماهنگی وجود دارد. از جمله فیثاغوریان گمان میکردند فاصلهٔ بین اجرام آسمانی را تا زمین در فضای کیهانی میتوان با نسبتهای معینی پیدا کرد. به همین دلیل بود که در مکتب فیثاغوری به بررسی دقیق نسبتها پرداختند. آنها به بررسی تصاعد حسابی، هندسی و همساز پرداختند.
از آنجا که بنیان فلسفی مجمع فیثاغوری بر آموزش رازهای عدد قرار گرفت، پیشرفتهای آنها در نظریه اعداد تعجبآور نیست.
هیپاسوس از فیثاغوریان متاخر بود که با کشف اعداد گنگ، باور به نقش اعداد را تا حدودی مخدوش کرد.
نمادهای فیثاغوری
فیثاغوریان نمادهای مختلفی را برای اشاره به اعداد، و بیان ارتباط میان اعداد و جهان ابداع کرده بودند که مهمترین از این نمادها عبارتند از:
 موناد
موناد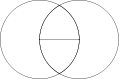 دیاد
دیاد تریاد
تریاد تتراد
تتراد پنتاد
پنتاد دکاد
دکاد تتراکتیس
تتراکتیس وسیکا پیسکیس
وسیکا پیسکیس
تناسخ و محرّمات
پس از فیثاغورس، گروهی از شاگردانش آیینی خیال آلوده و آشفته تشکیل دادند.[3] فیثاغوریان به تناسخ ارواح اعتقاد پیدا کردند، و چیزهای زیادی را به عنوان محرّمات در نظر گرفتند.[1] دینی تشکیل دادند که از جمله احکام آن میتوان به این موارد اشاره کرد:
- خوردن حبوبات حرام است.
- دست زدن به خروس سفید حرام است.
- نگاه کردن در آینهای که کنار چراغی باشد، حرام است.
- چیدن تاج گل حرام است.
- هنگامی که از رختخواب برمیخیزید، واجبست اثر بدنتان روی آن را صاف کنید.[3]
ریشههای شرقی دانش فیثاغوریان
کالین رنان، پژوهشگر و نویسندهٔ چند کتاب دربارهٔ تاریخ علم و از نویسندگان دانشنامهٔ بریتانیکا، در کتاب تاریخ علم کمبریج، به گوشههایی از ریشههای شرقی دانش یونانیان اشاره کردهاست:
فیثاغورس در جوانی از مصر و بابل دیدن کرد و شاید همین دیدار بود که به او انگیزه داد ریاضیات بخواند و بگوید همه چیز عدد است. او جبر، هندسه و هارمونی را از تمدن میانرودان آموخت.[4]
فیثاغورس میتوانست قانون ۳-۴-۵ را که دربارهٔ طول ضلعهای مثلث قائم الزاویهاست، از مصریان آموخته باشد، اما پژوهشهای اخیر نشان میدهد که در بابل به چیزی برخورد که ما آن را نسبت فیثاغورسی مینامیم. بابلیها پی برده بودند که عدهای نسبت میتوانند ۳-۴-۵ یا ۶-۸-۱۰ یا ترکیبی از این دست باشند که اگر بزرگترین عددش مربع شود برابر مجموع مربعهای دو عدد دیگر خواهد بود. این گام بلندی به جلو بود که فیثاغورسیان بهخوبی از آن بهره گرفتند.[1]
جنبهٔ دیگری که فیثاغورسیان فریفتهاش بودند؛ میانهها بود. نخست آنها در فکر میانهٔ عددی بودند (یعنی عدد میانی در تصاعد عددی سه جملهای. برای مثال، در تصاعد ۴، ۵، ۶، میانه عدد ۵ و در تصاعد ۴، ۸، ۱۲، میانه ۸ است). بعید نیست که این را فیثاغورس در سفرش به بابل آموخته باشد.[1]
اخترشناسی فیثاغورسی آشکارا بدهی فراوانی به بابلیها داشت.[1]
جستارهای وابسطه
پانویس
- رجینالد هالینگ دیل (۱۳۸۷)، «۸»، تاریخ فلسفه غرب، ترجمهٔ عبدالحسین آذرنگ، تهران: انتشارات ققنوس، ص. صفحه ۹۵ و ۹۶ و ۹۷
- Carl B. Boyer, A history of mathematics, page 49, 1991
- برتراند راسل (۱۳۴۰)، «۳»، تاریخ فلسفه غرب، جلد اول:فلسفه قدیم، ترجمهٔ نجف دریابندری، تهران: شرکت سهامی کتابهای جیبی، ص. صفحهٔ ۳۹
- Carl B. Boyer, A history of mathematics, page 56, 1991