رویه مربعی

در هندسهٔ تحلیلی، رویه‌های درجهٔ دوم در فضای سه‌بعدی دسته‌ای از رویه‌ها هستند که به این صورت تعریف می‌شوند: مکان هندسی همهٔ نقاطی مانند ${\displaystyle P=(x,y,z)}$ که در معادلهٔ ${\displaystyle F(x,y,z)=0}$ صدق کنند که ${\displaystyle F}$ یک تابع درجهٔ دو است[1].

به عنوان مثال کُره یک رویهٔ درجه دو است؛ زیرا معادلهٔ استاندارد کره یک معادلهٔ درجه دو است: ${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}}$

به طور کلّی‌تر، ابررویه‌های درجه دو در فضای ${\displaystyle \mathbb {R} ^{n}}$ دسته‌ای از ابررویه‌های ${\displaystyle n-1}$-بعدی هستند که به این صورت تعریف می‌شوند: مجموعهٔ همهٔ نقاطی مانند ${\displaystyle P=(x_{1},x_{2},\dots ,x_{n})}$ که در معادلهٔ ${\displaystyle F(x_{1},x_{2},\dots ,x_{n})=0}$ صدق کنند که ${\displaystyle F}$ یک تابع درجهٔ دو است.

در نتیجه می‌توان مقاطع مخروطی را حالت خاصی از رویه‌های درجه دو (حالت ${\displaystyle n=2}$) دانست. البتّه در فضای دوبعدی به جای «رویه» باید از اصطلاح «خم» استفاده کرد.

در سه بعد

در فضای سه‌بعدی، رویه‌های درجه دو به شاخه‌های زیر تقسیم می‌شود[1]:

بیضی‌گون	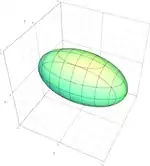${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}$
سهمی‌گون بیضوی	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}={z \over c}\,}$
سهمی‌گون هذلولوی	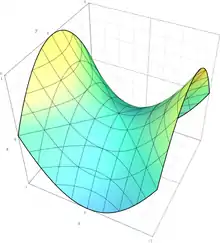${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}={z \over c},\quad c>0\,}$
هذلولی‌گون یکپارچه	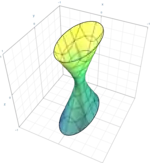${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}$
هذلولی‌گون دوپارچه	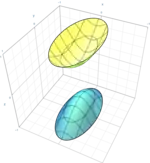${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}$

حالات حدّی یا تبهگنی
مخروط بیضوی	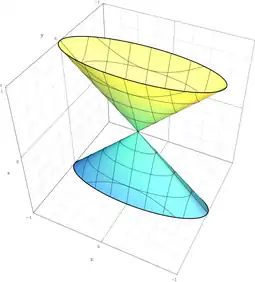${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}$
استوانهٔ بیضوی	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}$
استوانهٔ هذلولوی	${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}$
استوانهٔ سهموی	${\displaystyle x^{2}+2ay=0\,}$

وقتی که دو یا هر سه ثابت (${\displaystyle a}$ و ${\displaystyle b}$ و ${\displaystyle c}$) با یکدیگر برابر باشند، رویهٔ درجه دو دورانی به دست می‌آید:

حالات خاص: رویهٔ دورانی
کره‌گون	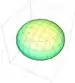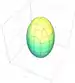${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,}$
کره	${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}\,}$
سهمی‌گون دایروی	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}$
هذلولی‌گون دورانی یکپارچه	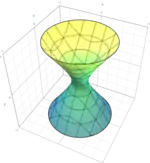${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=1\,}$
هذلولی‌گون دورانی دوپارچه	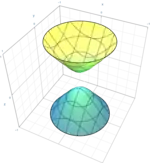${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=-1\,}$
سطح مخروطی	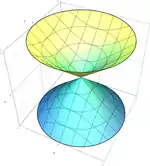${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=0\,}$
استوانه (دایروی)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}$

جستارهای وابسته

• رویه
• مقاطع مخروطی

منابع

1. «۱۲٫۶». Thomas' Calculus (14th Edition).