نظریه یادگیری محاسباتی

نظریه یادگیری محاسباتی(به انگلیسی : Computational Learning Theory) شاخه‌ای از ریاضیات و علوم رایانه است که به ارزیابی کارایی الگوریتم‌های یادگیری ماشینی می‌پردازد. این نظریه عموماً به تحلیل الگوریتم‌های یادگیری با نظارت می‌پردازد و سعی می‌کند کران‌هایی برای کارایی یک الگوریتم در داده دیده‌نشده با استفاده از اطلاعات کارایی آن الگوریتم در داده در دسترس و پیچیدگی الگوریتم بیابد. بعد وی‌سی و یادگیری صحیح احتمالی تخمینی مثال‌هایی از نظریه یادگیری محاسباتی هستند که به ترتیب به اختراع الگوریتم‌های ماشین بردار پشتیبانی و بوستینگ انجامیدند. این نظریه به تحلیل پیچیدگی زمانی الگوریتم‌های یادگیری نیز می‌پردازد. [1]

در این شکل یادگیر، باید به وسیله نمونه‌های ورودی آموزش ببیند که نمونه‌های درون مستطیل، به عنوان مثال دارای c(x) = 1 می‌باشند و برای بقیه نمونه‌ها ،c(x) = 0 می‌باشد.

مقدمه

همچنین این تئوری به دنبال جواب سوالاتی مانند "تحت چه شرایطی یادگیری موفق، ممکن یا ناممکن است؟" ویا "تحت چه شرایطی یک الگوریتم یادگیری خاص موفقیت یادگیری را تضمین می‌کند؟" می‌باشد. دو چهارچوب برای بررسی یادگیری الگوریتم‌های یادگیری در نظر گرفته می‌شود. چهارچوب اول، چهارچوب تقریباً درست یا PAC که در بالا اشاره ‌‌شد، می‌باشد. در این چهارچوب کلاس فرضیه‌هایی را که می‌توان یا نمی‌توان با تعداد چندجمله‌ایی از نمونه‌های آموزشی یادگرفت را بررسی می‌کند و معیاری طبیعی برای پیچیدگی فضای فرضیه‌ای که تعداد نمونه‌های آموزشی برای یادگیری استقرایی را محدود می‌کند، تعریف می‌کنیم. در چهارچوب کران خطا تعداد خطاهای آموزشی ای را که یادگیر قبل از تعیین فرضیه درست انجام می‌دهد را بررسی می‌کنیم. در مطالعه یادگیری ماشین، این سؤال طبیعی است که بپرسیم :

• چه قوانین کلی‌ای بر یادگیری‌های ماشین( یا حتی غیر ماشین) حاکم است؟
• آیا می‌توان تعداد نمونه‌های لازم برای اینکه یادگیری حتماً موفق شود را تعیین کرد؟
• آیا می‌توان تعداد خطاهای یادگیر قبل از یادگیری تابع هدف را مشخص کرد؟
• آیا می‌توان پیچیدگی ذاتی کلاس‌های مسائل مختلف را مشخص کرد؟

اگر چه جواب جامع همه این سوالات هنوز معلوم نیست، اما این قسمت از هوش محاسباتی برای پاسخ به این سوالات به وجود آمده‌است. برای مثال مسئله یادگیری استقرایی تابع هدفی نامعلوم از نمونه‌های آموزشی این تابع هدف و فضای فرضیه معلوم را در نظر بگیرید. در این مثال پاسخ به سوالاتی مثل تعداد نمونه‌های لازم برای یادگیری موفق و تعداد اشتباهات قبل از یادگیری کامل مطرح می‌شود. برای تعیین مرزهای این کمیت‌ها به ویژگی‌های مسئله‌ یادگیری از جمله موارد زیر بستگی دارد :‌

• اندازه یا پیچیدگی فضای فرضیه‌ای در نظر گرفته شده
• دقت لازم برای یادگیری
• احتمال اینکه یادگیر فرضیه‌ای موفق را خروجی دهد
• روند ارائه نمونه‌ها

در اکثر موارد ما بر روی الگوریتم یادگیری خاصی تمرکز نمی‌کنیم و ترجیح می‌دهیم بیشتر بر روی کلاس‌های الگوریتم‌های یادگیری با خواص یکسان (فضای فرضیه‌ای مشابه، نحوه نمایش نمونه‌های آموزشی مشابه و ...) بحث کنیم. در اکثر موارد سوالات بالا مطرح هستند. توجه کنید روش‌های گوناگونی برای تعریف موفق وجود دارد. ممکن است یادگیری فرضیه‌ای را موفق بدانیم که خروجی آن دقیقا مشابه هدف باشد، همچنین ممکن است یادگیری‌ای را موفق بدانیم که فرضیه اش در اکثر موارد مشابه هدف باشد. [2]

مدل یادگیری یک فرضیه تقریباً درست (PAC)

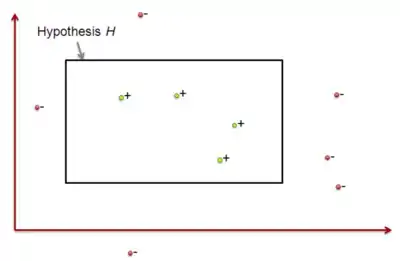
در این بخش، حالت خاصی را برای مسائل یادگیری در نظر می‌گیریم، این حال مدل یادگیری تقریباً درست (PAC) نامیده می‌شود. برای سادگی کار، یادگیری مفاهیم منطقی از داده‌های آموزشی بدون خطا را در نظر بگیرید. با این وجود بسیاری از نتایج حاصل را می‌توان به حالت کلی یادگیری توابع حقیقی مقادیر تابع هدف تعمیم داد. همچنین بسیاری دیگر از نتایج را می‌توان به یادگیری از انواع خاصی از داده‌های خطادار تعمیم داد. فرض کنید ${\displaystyle X}$ مجموعه‌ای از تمامی نمونه‌های ممکن بر روی تابع هدف مفروض باشد. برای مثال، مجموعه تمامی افراد با ویژگی‌های سن (پیر و جوان) و قد (بلند و کوتاه) باشد. ${\displaystyle C}$ مجموعه مفاهیم هدفی است که ممکن است، یادگیر برای یادگیری آن‌ها برای یادگیری آنها، به کار برده باشد. هر مفهوم هدف ${\displaystyle c}$ در مجموعه ${\displaystyle C}$ متناسب با زیر مجموعه‌ای از ${\displaystyle X}$ است. به‌طور مشابه ${\displaystyle c}$ متناسب با تابع ${\displaystyle c:X\rightarrow \{0,1\}}$ می‌باشد. برای مثال، یک تابع هدف ${\displaystyle c}$ در ${\displaystyle C}$، ممکن است مفهوم افراد اسکی باز باشد. اگر ${\displaystyle x}$ نمونه مثبتی از ${\displaystyle c}$ باشد، داریم : [3]

${\displaystyle c(x)=0}$

در این حالت فرض می‌کنیم که نمونه‌ها به صورت تصادفی و با توزیع احتمال ${\displaystyle D}$ انتخاب می‌شوند. برای مثال، ${\displaystyle D}$ ممکن است، توزیع احتمال نمونه افرادی باشد که از یک باشگاه ورزشی بیرون می‌آیند (توزیع احتمالی بر روی تمامی افراد). در کل ${\displaystyle D}$ ممکن است، هر توزیع احتمالی باشد و درحالت کلی این توزیع برای یادگیر ناشناخته است. تمامی اطلاعات موجود در ${\displaystyle D}$ این است که توزیع احتمالی ثابت است، بدین معنا که این توزیع احتمال با زمان تغییر نمی‌کند. نمونه‌های آموزشی با این توزیع احتمال انتخاب شده و به همراه مقدار تابع هدفشان (${\displaystyle c(x)}$) به یادگیر داده می‌شوند.

این شکل تعریف خطای PAC را نشان می‌دهد. مفاهیم c و h با مجموعه نمونه‌های X نمایش داده شده‌اند. نمونه‌های آموزشی در این مثال با علامت‌های مثبت و منفی نشان داده شده‌اند. خطای h برای c، احتمال دسته بندی غلط نمونه تصادفی در این صفحه یا قرار گرفتن در اختلاف این دو مجموعه (نواحی هلالی شکل) می‌باشد.

یادگیر ${\displaystyle L}$ مجموعه‌ای از فرضیه‌های ممکن مانند ${\displaystyle H}$ را در یادگیری مفهوم هدف در نظر می‌گیرد. برای مثال، ${\displaystyle H}$ ممکن است، مجموعه تمامی فرضیه‌های قابل بیان به صورت عطف سن و قد باشد. بعد از مشاهده یک سری از نمونه‌های آموزشی، برای تابع هدف ${\displaystyle c}$، باید فرضیه‌ای مانند ${\displaystyle h}$ از ${\displaystyle H}$ که تخمین آن از ${\displaystyle c}$ است، به عنوان فرضیه‌ تخمینی خروجی دهد. موفقیت ${\displaystyle L}$ را کارایی این فرضیه ${\displaystyle h}$ بر روی نمونه‌های جدیدی که به صورت تصادفی از ${\displaystyle X}$ و باتوزیع ${\displaystyle D}$ انتخاب می‌شوند، می‌سنجیم. در چنین حالتی، علاقه ما به کارایی یادگیرهای مختلف ${\displaystyle L}$ با فضای فرضیه‌های مختلف ${\displaystyle H}$ در یادگیری مجموعه توابع هدف مختلف درون ${\displaystyle C}$ است. زیرا ما می‌خواهیم یادگیر ${\displaystyle L}$ به اندازه کافی جامع باشد تا بتواند هر تابع هدف درون ${\displaystyle C}$ را مستقل از اینکه توزیع ${\displaystyle D}$ چیست، یاد بگیرد. در بعضی مواقع نیز علاقه داریم که بدترین حالت توابع هدف درون ${\displaystyle C}$ را برای تمامی توزیع‌های ${\displaystyle D}$ بررسی کنیم. چون علاقه ما به نزدیکی فرضیه خروجی ${\displaystyle h}$ به تابع هدف حقیقی ${\displaystyle c}$ است، پس کار را با تعریف خطای واقعی یک فرضیه ${\displaystyle h}$ بر روی ${\displaystyle c}$ و توزیع احتمال ${\displaystyle D}$ شروع می‌کنیم. خطای واقعی ${\displaystyle h}$، حطای ${\displaystyle h}$ در دسته‌بندی نمونه‌های جدید با توزیع ${\displaystyle D}$ است.

تعریف :‌ خطای واقعی(${\displaystyle error_{D}(h)}$) فرضیه ${\displaystyle h}$ برای تابع هدف ${\displaystyle c}$ و توزیع احتمال نمونه ${\displaystyle D}$ این است که نمونه انتخابی بر اساس توزیع ${\displaystyle D}$ اشتباه دسته‌بندی شود. (در رابطه زیر، ${\displaystyle Pr_{x\in D}}$ نشان دهنده احتمال عبارت با فرض اینکه ${\displaystyle x}$ از توزیع ${\displaystyle D}$ پیروی می‌کند، می‌باشد.

${\displaystyle error_{D}(h)\equiv Pr_{x\in D}[c(x)\not =h(x)]}$

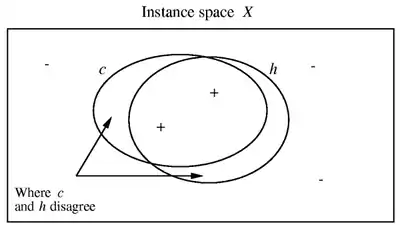
توجه کنید که خطا را طوری تعریف کرده ایم که که خطای تمامی نمونه‌های ممکن را اندازه بگیرد و فقط محدود به نمونه‌های آموزشی نباشد. بنابراین انتظار داریم که زمانی که از فرضیه بدست آمده بر روی نمونه‌های تصادفی جدید استفاده می‌کنیم، چنین خطایی داشته باشد. همچنین توجه کنید که این خطا به شدت به توزیع احتمال ${\displaystyle D}$ وابسته است. برای مثال، اگر ${\displaystyle D}$ توزیعی یکنواخت باشد که به تمامی نمونه‌های ${\displaystyle X}$ احتمالی یکسان نسبت می‌دهد، خطای فرضیه آمده در شکل روبرو نسبت به نمونه‌های درون نواحی هلالی به تمامی نمونه‌ها خواهد بود. در نتیجه اگر ${\displaystyle D}$ احتمال بیشتری به نمونه‌های نواحی هلالی نسبت دهد، خطا بیشتر خواهد شد. در بدترین حالت نیز،${\displaystyle D}$، احتمال صفر به نمونه‌های خارج نواحی هلالی و احتمال ۱ به نمونه‌های درون نواحی هلالی نسبت می‌دهد و خطا ۱ خواهد بود، با وجود اینکه ${\displaystyle c}$ و ${\displaystyle h}$ واقعا اشتراک دارند. توجه داشته باشید که خطای ${\displaystyle h}$ برای ${\displaystyle c}$ به‌طور مستقیم، برای یادگیر غیرقابل مشاهده است. ${\displaystyle L}$ فقط کارایی ${\displaystyle h}$ را بر روی نمونه‌های آموزشی، در دسترس دارد و باید انتخاب خود در مورد فرضیه را بر اساس همین معیار انجام دهد. ما از عبارات خطای آموزشی (در مقابل خطای واقعی) برای نمایش نسبت نمونه‌های آموزشی با دسته‌بندی اشتباه توسط ${\displaystyle h}$ به کل نمونه‌های آموزشی استفاده می‌کنیم. قسمت بزرگی از بررسی ما از پیچیدگی یادگیری بر محور این سؤال متمرکز می‌شود که چگونه احتمال دارد که خطای آموزشی مشاهده شده، معیاری غلط‌انداز از ${\displaystyle error_{D}(h)}$ باشد؟ است. [4]

مدل یادگیری مرز خطا

با وجود اینکه تمرکز، بیشتر بر مدل PAC می‌باشد،‌ تئوری یادگیری محاسباتی تعریف مسئله‌های دیگر را در بر می‌گیرد. تعریف مسئله‌های یادگیری مختلفی که مورد مطالعه قرار گرفته‌است، در نحوه ایجاد نمونه‌های یادگیری، نویز داده‌ها(با خطا یا بدون خطا)، تعریف موفق (مفهوم هدف باید یاد گرفته شود یا اینکه تقریباً با احتمال خاصی یادگرفته شود.)، فرض‌های یادگیر(شامل توزیع نمونه‌ای و اینکه ${\displaystyle C\subseteq H}$) و معیاری که با آن یادگیر ارزیابی می‌شود (مانند تعداد نمونه‌های آموزشی، تعداد اشتباه‌ها، زمان کل یادگیری و ...)، متفاوت است. در این مدل، یادگیر با تعداد اشتباه‌هایش قبل از همگرایی به فرضیه درست، ارزیابی می‌شود. مشابه تعریف مسئله در مدل PAC، فرض کنید، یادگیر یک سری از نمونه‌های آموزشی را دریافت ‌‌می‌کند. با این وجود، در اینجا می‌خواهیم یادگیر، قبل از دریافت هر نمونه ${\displaystyle x}$، مقدار تابع هدف ${\displaystyle c(x)}$ را(قبل از معلوم شدن مقدار درست هدف) پیش‌بینی کند. حال سؤال این است که یادگیر قبل از یادگیری مفهوم هدف چه تعداد پیش‌بینی اشتباه خواهد کرد؟. اهمیت این سؤال در کاربرد عملی است، زیرا که یادگیری باید زمانی که سیستم در حال استفاده واقعی است، انجام شود، نه در مرحله آموزشی مجزا. برای مثال، اگر سیستم برای یادگیری پیش‌بینی اینکه چه پرداخت‌هایی برای یک کارت اعتباری باید ثبت شود و چه پرداخت‌‌،‌هایی تقلبی هستند، بر اساس اطلاعاتی که در حین استفاده از سیستم، جمع‌آوری می‌کند، طراحی می‌شود. بنابراین علاقه خواهیم داشت که تعداد اشتباهات قبل از همگرایی به تابع هدف کمینه شود. در اینجا تعداد کل اشتباهات، می‌تواند اهمیت بیشتری نسبت به تعداد کل نمونه‌های آموزشی داشته باشد. این مسئله یادگیری مرز خطا را می‌توان در شرایط خاص مختلفی مورد مطالعه قرار داد. برای مثال، ممکن است تعداد اشتباهات قبل از یادگیری PAC تابع هدف را بشماریم. اما در اکثر مثال‌ها قبل از اینکه یادگیر، مفهوم هدف را دقیقا یاد بگیرد، تعداد اشتباه‌ها را در نظر می‌گیریم. یادگیری مفهوم هدف به این معناست که به فرضیه‌ای میل کنیم که داشته باشیم: [2] ${\displaystyle \forall {x\in X}:h(x)=c(x)}$

جستارهای وابسته

• هوش مصنوعی (Artificial Intelligence)
• هوش محاسباتی (Computational Intelligence)
• یادگیری ماشین (Machinelearning)
• شبکه عصبی مصنوعی (Artificial Neural Network)
• یادگیری عمیق (Deep Learning)
• یادگیری تقویتی (Reinforcement learning)
• یادگیری بانظارت (Supervised learning)

منابع

1. Angluin, D (1992). "Computational learning theory: Survey and selected bibliography". In Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing: 351–354.
2. Mitchell, Tom (1997). Machine Learning. McGraw Hill Education. ISBN 0-070-42807-7.
3. Kivinen, Jyrki; H.Sloan, Robet (2012). Computational Learning Theory: 15th Annual Conference on Computational Learning Theory. Springer. ISBN 3-540-43836-X.
4. J.Kearns, Michael; V.Vazirani, Mesh (1994). An Introduction to Computational Learning Theory. The MIT Press. ISBN 0-262-11193-4.

پیوند به بیرون

• انجمن نظریه یادگیری محاسباتی
• درس مقدمه‌ای بر نظریه یادگیری محاسباتی دانشگاه MIT
• درس نظریه یادگیری محاسباتی دانشگاه پنسیلوانیا (Michael Kearns)