دایره محیطی
در هندسه، دایره محیطی (به انگلیسی: Circumscribed Circle) (یا Circumcircle) از یک چندضلعی، دایره ای است که از تمام رئوس آن چندضلعی میگذرد. مرکز این دایره را «مرکز دایره محیطی» (Circumcenter) و شعاعش را «شعاع دایره محیطی» (Circumradius) مینامند.
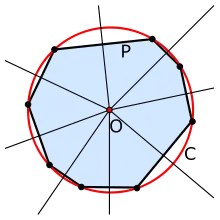
همه چندضلعیها لزوماً دایره محیطی ندارند. چندضلعی که دایره محیطی داشته باشد را «چندضلعی محاطی» (چون توسط یک دایره احاطه شده)، «چندضلعی دایرهای» (Cyclic Polygon)، یا «چندضلعی همدایره» (Concyclic Polygon) نیز مینامند، چرا که رئوس آن همدایره اند. تمام مثلثها، تمامی چندضلعیهای ساده منتظم، تمام مستطیلها، تمام ذوزنقههای متساوی الساقین، و همچنین تمام کایتهای راستگوشه جزو چندضلعیهای محاطی اند.
مفهوم مرتبط با آن، «دایره احاطهکننده کمینه» است، یعنی کوچکترین دایرهای که خود چندضلعی را کاملاً در بر گیرد، به طوری که مرکز دایره داخل چندضلعی قرار گیرد. هر چندضلعی دارای چنین دایرهی منحصربفردی است که میتوان آن را با الگوریتم زمان-خطی ساخت.[1] حتی اگر یک چندضلعی دارای دایره محیطی باشد، ممکن است این دایره متفاوت با دایره احاطهکننده کمینهاش باشد. به عنوان مثال، برای یک مثلث منفرجه، قطر دایره احاطهکننده کمینه، همان ضلع بزرگ مثلث بوده و دایره مذکور نیز از رأس مقابل این ضلع عبور نمیکند.
مثلثها
تمام مثلثها دایرهای (یا دوری) اند؛ یعنی، هر مثلث دارای دایره محیطی است.
ترسیم با خطکش و پرگار
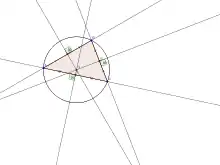
مرکز دایره محیطی یک مثلث را می توان با ترسیم دو عمود منصف دلخواه از آن بدست آورد. برای سه نقطه غیر-همخط (یعنی رئوس مثلث)، این دو خط نمیتوانند موازی باشند و مرکز دایره محیطی محل برخوردشان خواهد بود. هر نقطه روی عمود منصف از رأس انتهای ضلع مورد نظر به یک فاصله اند، در نتیجه محل برخوردشان (مرکز دایره محیطی) از هر سه رأس به یک فاصله میباشد، لذا شعاع دایره محیطی، فاصله آن از هر سه رأس مثلث است.
ترسیمی دیگر
روش دیگر جهت تعیین مرکز دایره محیطی این است که دو خط ترسیم شده، به گونهای که هر کدام طبق شکل از دو رأس دلخواه، با زاویه (مجاور با ضلع مشترک بینشان) برابر با °90 منهای زاویه رأس مقابل با ضلع مشترک خارج شوند (در حالتی که زاویه آلفای مربوط به رأس مقابل، زاویه منفرجهای باشد، ترسیم خطی با زاویه منفی به معنای این است که خطوط به سمت خارج مثلث کشیده میشوند، چرا که در این حالت مرکز دایره محیطی بیرون مثلث قرار میگیرد).
برخی مواقع در ناوبری ساحلی، هنگامی که قطبنما در دسترس نباشد، از دایره محیطی مثلث به عنوان روشی جهت بدست آوردن خط موقعیت با استفاده از سکستانت استفاده می شود. زاویه افقی بین دو علامت مشخصه روی زمین، دایره محیطی را براساس موقعیت ناظر تعریف مینماید.
مختصات کارتزین
در صفحه اقلیدسی، امکان ارائه معادله صریحی از دایره محیطی برحسب مختصات کارتزین رئوس مثلث محاط در آن وجود دارد. فرض کنید:
مختصات نقاط A، B، و C باشند. آنگاه دایره محیطی مکان هندسی نقاط در صفحه کارتزین خواهد بود که در معادلات زیر صدق میکند:
معادلات بالا تضمین میکنند که همه نقاط A، B، C، و v دارای فاصله مساوی r از مرکز مشترک u دایره میباشند. میتوان با استفاده از اتحاد قطبش، این معادلات را به شرط ناصفر بودن هسته ماتریس زیر تقلیل داد:
لذا، ممکن است بتوان دایره محیطی را به صورت مکان هندسی صفرهای دترمینان این ماتریس توصیف نمود:
با استفاده از بسط کوفاکتور، فرض کنید:
سپس داریم و با فرض این که سه نقطه همخط نباشند (در غیر این صورت دایره محیطی، همان خطی است که میتوان آن را به عنوان دایره تعمیم یافته ای دید که S آن در بینهایت قرار دارد)، معادله ، به ما مرکز دایره محیطی و شعاع دایره محیطی را خواهد داد. رهیافت مشابهی امکان بدست آوردن معادلات مربوط به کره محیطی یک چهاروجهی را خواهند داد.
معادله پارامتری
بردار واحد عمود بر صفحه در بر گیرنده دایره به این صورت است:
ازین رو، اگر شعاع r، مرکز، ، نقطهای روی دایره، و بردار نرمال واحد از صفحهی شامل دایره داده شده باشد، معادله تک پارامتری دایره که از شروع شده و در جهت مثبت (یعنی در جهت راست-دست) حول پیش رود، به صورت زیر خواهد بود:
مختصات سهخطی و گرانیگاهی
معادله ای برای دایره محیطی در مختصات سهخطی به این صورت است:[2] . معادله آن در مختصات گرانیگاهی به این صورت است: .
مزدوج ایزوگونال دایره محیطی، خط در بینهایت بوده که در مختصات سهخطی به صورت و در مختصات گرانیگاهی به صورت است.
ابعاد بالاتر
دایره محیطی یک مثلث که در بعد d نشانده شده است را می توان با استفاده از روش تعمیم یافته پیدا نمود. فرض کنید و و نقاط d-بعدی بوده که تشکیل مثلث میدهند. با انتقال دستگاه شروع میکنیم تا به مبدأ مختصات منتقل شود:
سپس شعاع دایره محیطی، r، به این صورت خواهد بود:
که در آن زاویه داخلی بین و است. مرکز دایره محیطی، به این صورت داده شده است:
این فرمول تنها در سه بعد کار میکند، چرا که ضرب خارجی در ابعاد دیگر تعریف نشده، اما میتوان آن را با جایگزین کردن ضرب داخلی با اتحادهای زیر تعمیم داد:
منابع
- Megiddo, N. (1983). "Linear-time algorithms for linear programming in R3 and related problems". SIAM Journal on Computing. 12 (4): 759–776. doi:10.1137/0212052.
- Whitworth, William Allen (1866). Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. Deighton, Bell, and Co. p. 199.
پیوندهای بیرونی
- Derivation of formula for radius of circumcircle of triangle at Mathalino.com
- Semi-regular angle-gons and side-gons: respective generalizations of rectangles and rhombi at Dynamic Geometry Sketches, interactive dynamic geometry sketch.
MathWorld
تعاملی
- Triangle circumcircle and circumcenter With interactive animation
- An interactive Java applet for the circumcenter