چندضلعی منتظم

در هندسه اقلیدسی، یک چندضلعی منتظم، چندضلعی است که همه زوایا و اضلاع آن هم‌اندازه‌اند.

مجموعه n-ضلعی‌های منتظم کوژ
چندضلعی‌های منتظم
ضلع و رأس	n
نماد	{n}
گروه تقارن	D_n, order 2n
چندضلعی همزاد	خود همزاد
مساحت (با a=طول ضلع)	$A={\tfrac {1}{4}}na^{2}\cot {\frac {\pi }{n}}$
زاویه داخلی	$(n-2)\times {\frac {180^{\circ }}{n}}$
مجموع زوایای داخلی	$\left(n-2\right)\times 180^{\circ }$
ویژگی‌ها	کوژ، سیکلیک، متساوی‌الاضلاع، Isogonal، Isotoxal

چندضلعی‌های منتظم، می‌توانند کوژ یا به شکل ستاره باشند. در حالت حدی، یک دنباله از چندضلعی‌های منتظم با افزایش تعداد اضلاع، در صورت ثابت ماندن محیط به دایره تبدیل می‌شود و در صورت ثابت ماندن طول ضلع، به apeirogon تبدیل می‌شود.

ویژگی‌ها

ویژگی‌های بیان‌شده در ادامه، برای همهٔ چندضلعی‌های منتظم (اعم از کوژ و ستاره‌ای) برقرار است.

یک چندضلعی منتظم n-ضلعی، تقارن چرخشی از مرتبهٔ n دارد.

همهٔ رأس‌های یک چندضلعی منتظم بر روی یک دایره (دایره محیطی) قرار می‌گیرند. به‌عبارت دیگر، رأس‌ها نقاطی هم‌دایره هستند. یعنی یک چندضلعی منتظم، لزوماً یک چندضلعی دایره‌ای هم هست.

هر چندضلعی منتظم، یک دایره محاطی دارد که به همه اضلاع در نقطهٔ وسط آنها مماس است. بنابراین هر چندضلعی منتظم، لزوماً یک چندضلعی مماسی هم هست.

یک n-ضلعی منتظم با استفاده از خط‌کش و پرگار قابل ترسیم است؛ اگر و تنها اگر فاکتورهای اول فرد n، اعداد اول فرمای متفاوتی باشند.

چندضلعی های منتظم محیطی، بیشترین مساحت را در دایره دارند. به عنوان مثال بین همه‌ی سه ضلعی های محیطی در یک دایره مثلث متساوی الاضلاع و در بین همه ی چهار ضلعی های محیطی در یک دایره مربع بیشترین مساحت را دارد.

چندضلعی‌های منتظم کوژ

همهٔ چندضلعی‌های سادهٔ منتظم، کوژ هستند. چندضلعی‌های منتظم باتعداد اضلاع یکسان، متشابه هستند. یک n-ضلعی منتظم کوژ، با نماد شلفلی {n} نشان داده می‌شود.

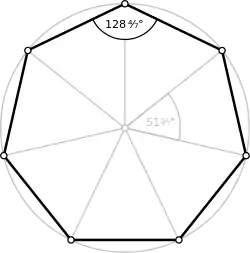
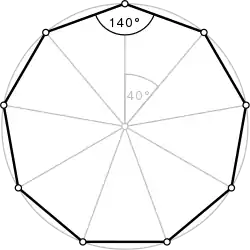
مثلث متساوی‌الاضلاع {۳}	مربع {۴}	پنج‌ضلعی {۵}	شش‌ضلعی {۶}	هفت‌ضلعی {۷}	هشت‌ضلعی {۸}	نه‌ضلعی {۹}	ده‌ضلعی {۱۰}
یازده‌ضلعی {۱۱}	دوازده‌ضلعی {۱۲}	سیزده‌ضلعی {۱۳}	چهارده‌ضلعی {۱۴}	پانزده‌ضلعی {۱۵}	شانزده‌ضلعی {۱۶}	هفده‌ضلعی {۱۷}	هجده‌ضلعی {۱۸}	نوزده‌ضلعی {۱۹}
بیست‌ضلعی {۲۰}	سی‌ضلعی {۳۰}	چهل‌ضلعی {۴۰}	پنجاه‌ضلعی {۵۰}	شصت‌ضلعی {۶۰}	هفتادضلعی {۷۰}	هشتادضلعی {۸۰}	نودضلعی {۹۰}	صدضلعی {۱۰۰}

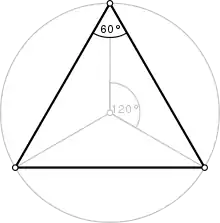
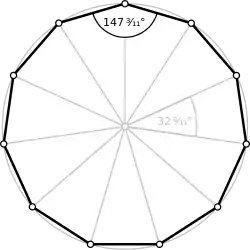
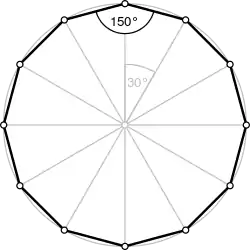
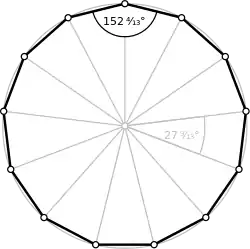
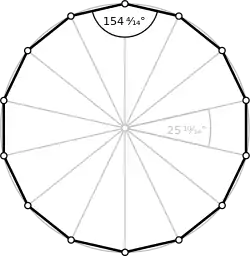
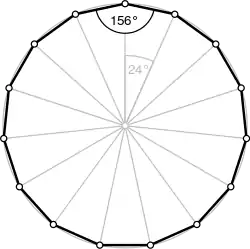
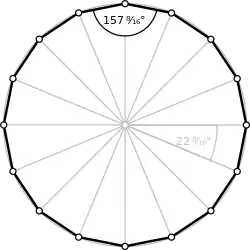
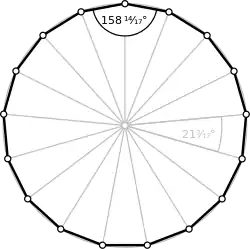
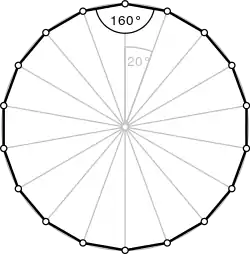
زاویه‌ها

برای یک n-ضلعی منتظم کوژ، اندازهٔ هر زاویهٔ داخلی برابر است با:

\left(1-{\frac {2}{n}}\right)\times 180

یا

(n-2)\times {\frac {180}{n}}

درجه

یا ${\frac {(n-2)\pi }{n}}$ رادیان

و اندازهٔ هر زاویه خارجی آن برابر است با ${\tfrac {360}{n}}$ درجه.

قطرها

برای n > ۲، تعداد قطرهای n-ضلعی، برابر است با ${\tfrac {n(n-3)}{2}}$ ، به‌عنوان مثال برای مثلث، چهارضلعی، پنج‌ضلعی و شش‌ضلعی، تعداد قطرها به‌ترتیب، ۰، ۲، ۵ و ۹ است.

برای یک n-ضلعی منتظم محاط‌شده در یک دایره به شعاع واحد، حاصل‌ضرب فاصلهٔ هر رأس تا همهٔ رأس‌های دیگر، برابر است با n.

مساحت

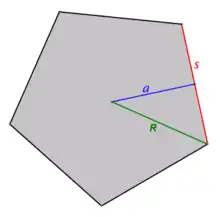
پنج‌ضلعی منتظم با طول ضلع s، شعاع دایره محیطی R و شعاع دایره محاطی a

مساحت یک n-ضلعی منتظم کوژ با اندازهٔ ضلع a، شعاع دایره محیطی R، شعاع دایره محاطی r و محیط p با استفاده از روابط زیر بدست می‌آید:[1][2]

(زوایا برحسب رادیان است.)

A={\tfrac {1}{2}}nar={\tfrac {1}{2}}pr={\tfrac {1}{4}}na^{2}\cot {\tfrac {\pi }{n}}=nr^{2}\tan {\tfrac {\pi }{n}}={\tfrac {1}{2}}nR^{2}\sin {\tfrac {2\pi }{n}}

که در آن R برابر است با:

R={\frac {s}{2\sin \left({\frac {\pi }{n}}\right)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\right)}}

مساحت یک چندضلعی منتظم با طول ضلع ۱، شعاع دایره محیطی ۱، شعاع دایره محاطی ۱ در جدول زیر ارائه شده‌است:

تعداد اضلاع	نام چندضلعی	مساحت با طول ضلع ۱		مساحت با شعاع دایره محیطی ۱			مساحت با شعاع دایره محاطی ۱
تعداد اضلاع	نام چندضلعی	دقیق	تقریبی	دقیق	تقریبی	تقریبی به‌صورت کسری از دایره	دقیق	تقریبی	تقریبی به‌صورت کسری از دایره
n	n-ضلعی منتظم	${\tfrac {n}{4}}\cot {\tfrac {\pi }{n}}$		${\tfrac {n}{2}}\sin {\tfrac {2\pi }{n}}$		${\tfrac {n}{2\pi }}\sin {\tfrac {2\pi }{n}}$	$n\tan {\tfrac {\pi }{n}}$		${\tfrac {n}{\pi }}\tan {\tfrac {\pi }{n}}$
۳	مثلث متساوی‌الاضلاع	$\sqrt 3 /4$	۰٫۴۳۳۰۱۲۷۰۲	$3 \sqrt 3 /4$	۱٫۲۹۹۰۳۸۱۰۵	۰٫۴۱۳۴۹۶۶۷۱۴	$3 \sqrt 3$	۵٫۱۹۶۱۵۲۴۲۴	۱٫۶۵۳۹۸۶۶۸۶
۴	مربع	۱	۱٫۰۰۰۰۰۰۰۰۰	۲	۲٫۰۰۰۰۰۰۰۰۰	۰٫۶۳۶۶۱۹۷۷۲۲	۴	۴٫۰۰۰۰۰۰۰۰۰	۱٫۲۷۳۲۳۹۵۴۴
۵	پنج‌ضلعی منتظم	$1/4 \sqrt 25+10 \sqrt 5$	۱٫۷۲۰۴۷۷۴۰۱	$5/4 \sqrt (5+ \sqrt 5)/2$	۲٫۳۷۷۶۴۱۲۹۱	۰٫۷۵۶۸۲۶۷۲۸۸	$5 \sqrt 5-2 \sqrt 5$	۳٫۶۳۲۷۱۲۶۴۰	۱٫۱۵۶۳۲۸۳۴۷
۶	شش‌ضلعی منتظم	$3 \sqrt 3 /2$	۲٫۵۹۸۰۷۶۲۱۱	$3 \sqrt 3 /2$	۲٫۵۹۸۰۷۶۲۱۱	۰٫۸۲۶۹۹۳۳۴۲۸	$2 \sqrt 3$	۳٫۴۶۴۱۰۱۶۱۶	۱٫۱۰۲۶۵۷۷۹۱
۷	هفت‌ضلعی منتظم		۳٫۶۳۳۹۱۲۴۴۴		۲٫۷۳۶۴۱۰۱۸۹	۰٫۸۷۱۰۲۶۴۱۵۷		۳٫۳۷۱۰۲۲۳۳۳	۱٫۰۷۳۰۲۹۷۳۵
۸	هشت‌ضلعی منتظم	$2+2 \sqrt 2$	۴٫۸۲۸۴۲۷۱۲۵	$2 \sqrt 2$	۲٫۸۲۸۴۲۷۱۲۵	۰٫۹۰۰۳۱۶۳۱۶۰	$8(\sqrt 2 -1)$	۳٫۳۱۳۷۰۸۵۰۰	۱٫۰۵۴۷۸۶۱۷۵
۹	نه‌ضلعی منتظم		۶٫۱۸۱۸۲۴۱۹۴		۲٫۸۹۲۵۴۴۲۴۴	۰٫۹۲۰۷۲۵۴۲۹۰		۳٫۲۷۵۷۳۲۱۰۹	۱٫۰۴۲۶۹۷۹۱۴
۱۰	ده‌ضلعی منتظم	$5/2 \sqrt 5+2 \sqrt 5$	۷٫۶۹۴۲۰۸۸۴۳	$5/2 \sqrt (5- \sqrt 5)/2$	۲٫۹۳۸۹۲۶۲۶۲	۰٫۹۳۵۴۸۹۲۸۴۰	$2 \sqrt 25-10 \sqrt 5$	۳٫۲۴۹۱۹۶۹۶۳	۱٫۰۳۴۲۵۱۵۱۵
۱۱	یازده‌ضلعی منتظم		۹٫۳۶۵۶۳۹۹۰۷		۲٫۹۷۳۵۲۴۴۹۶	۰٫۹۴۶۵۰۲۲۴۴۰		۳٫۲۲۹۸۹۱۴۲۳	۱٫۰۲۸۱۰۶۳۷۱
۱۲	دوازده‌ضلعی منتظم	$6+3 \sqrt 3$	۱۱٫۱۹۶۱۵۲۴۲	۳	۳٫۰۰۰۰۰۰۰۰۰	۰٫۹۵۴۹۲۹۶۵۸۶	$12(2- \sqrt 3)$	۳٫۲۱۵۳۹۰۳۰۹	۱٫۰۲۳۴۹۰۵۲۳
۱۳	سیزده‌ضلعی منتظم		۱۳٫۱۸۵۷۶۸۳۳		۳٫۰۲۰۷۰۰۶۱۷	۰٫۹۶۱۵۱۸۸۶۹۴		۳٫۲۰۴۲۱۲۲۲۰	۱٫۰۱۹۹۳۲۴۲۷
۱۴	چهارده‌ضلعی منتظم		۱۵٫۳۳۴۵۰۱۹۴		۳٫۰۳۷۱۸۶۱۷۵	۰٫۹۶۶۷۶۶۳۸۵۹		۳٫۱۹۵۴۰۸۶۴۲	۱٫۰۱۷۱۳۰۱۶۱
۱۵	پانزده‌ضلعی منتظم		۱۷٫۶۴۲۳۶۲۹۱		۳٫۰۵۰۵۲۴۸۲۲	۰٫۹۷۱۰۱۲۲۰۸۸		۳٫۱۸۸۳۴۸۴۲۶	۱٫۰۱۴۸۸۲۸۲۴
۱۶	شانزده‌ضلعی منتظم	$4 (1+ \sqrt 2 + \sqrt 2 (2+ \sqrt 2))$	۲۰٫۱۰۹۳۵۷۹۷	$4 \sqrt 2- \sqrt 2$	۳٫۰۶۱۴۶۷۴۶۰	۰٫۹۷۴۴۹۵۳۵۸۴	$16 (1+ \sqrt 2)(\sqrt 2 (2- \sqrt 2) -۱)$	۳٫۱۸۲۵۹۷۸۷۸	۱٫۰۱۳۰۵۲۳۶۸
۱۷	هفده‌ضلعی منتظم		۲۲٫۷۳۵۴۹۱۹۰		۳٫۰۷۰۵۵۴۱۶۳	۰٫۹۷۷۳۸۷۷۴۵۶		۳٫۱۷۷۸۵۰۷۵۲	۱٫۰۱۱۵۴۱۳۱۱
۱۸	هجده‌ضلعی منتظم		۲۵٫۵۲۰۷۶۸۱۹		۳٫۰۷۸۱۸۱۲۹۰	۰٫۹۷۹۸۱۵۵۳۶۱		۳٫۱۷۳۸۸۵۶۵۳	۱٫۰۱۰۲۷۹۱۸۱
۱۹	نوزده‌ضلعی منتظم		۲۸٫۴۶۵۱۸۹۴۳		۳٫۰۸۴۶۴۴۹۵۸	۰٫۹۸۱۸۷۲۹۸۵۴		۳٫۱۷۰۵۳۹۲۳۸	۱٫۰۰۹۲۱۳۹۸۴
۲۰	بیست‌ضلعی منتظم	$5 (1+ \sqrt 5 + \sqrt 5+2 \sqrt 5)$	۳۱٫۵۶۸۷۵۷۵۷	$5/2 (\sqrt 5 -1)$	۳٫۰۹۰۱۶۹۹۴۴	۰٫۹۸۳۶۳۱۶۴۳۰	$20 (1+ \sqrt 5 - \sqrt 5+2 \sqrt 5)$	۳٫۱۶۷۶۸۸۸۰۶	۱٫۰۰۸۳۰۶۶۶۳
۱۰۰	صدضلعی منتظم		۷۹۵٫۵۱۲۸۹۸۸		۳٫۱۳۹۵۲۵۹۷۷	۰٫۹۹۹۳۴۲۱۵۶۵		۳٫۱۴۲۶۲۶۶۰۵	۱٫۰۰۰۳۲۹۱۱۷
۱۰۰۰	هزارضلعی منتظم		۷۹۵۷۷٫۲۰۹۷۵		۳٫۱۴۱۵۷۱۹۸۳	۰٫۹۹۹۹۹۳۴۲۰۰		۳٫۱۴۱۶۰۲۹۸۹	۱٫۰۰۰۰۰۳۲۹۰
۱۰۰۰۰	ده‌هزارضلعی منتظم		۷۹۵۷۷۴۶٫۸۹۳		۳٫۱۴۱۵۹۲۴۴۸	۰٫۹۹۹۹۹۹۹۳۴۵		۳٫۱۴۱۵۹۲۷۵۷	۱٫۰۰۰۰۰۰۰۳۳
۱٬۰۰۰٬۰۰۰	میلیون‌ضلعی منتظم		۷۹٬۵۷۷٬۴۷۱٬۵۴۵٫۶۸۵		۳٫۱۴۱۵۹۲۶۵۴	۱٫۰۰۰۰۰۰۰۰۰		۳٫۱۴۱۵۹۲۶۵۴	۱٫۰۰۰۰۰۰۰۰۰

در بین همهٔ n-ضلعی‌ها با محیط داده‌شده، بیشترین مساحت مربوط به n-ضلعی منتظم است.[3]

چندضلعی‌های منتظم ستاره‌ای

یک ستاره پنج‌پر {5/2}

یک چندضلعی منتظم غیرکوژ، یک چندضلعی منتظم ستاره‌ای است. متداول‌ترین نمونه، ستاره پنج‌پر است که رأس‌های آن دقیقاً مشابه پنج‌ضلعی منتظم هستند، ولی هر رأس به دو رأس متفاوت با پنج‌ضلعی متصل شده است.

جستارهای وابسته

چندضلعی متساوی‌الاضلاع

پانویس

"Math Open Reference". Retrieved 4-Feb-2014. Check date values in: |accessdate= (help)
"Mathwords".
Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] "Math Open Reference". Retrieved 4-Feb-2014. Check date values in: |accessdate= (help)

[2] "Mathwords".

[3] Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.

چندضلعی‌ها
فهرست بر اساس تعداد ضلع
۱–۱۰ ضلعی	تک‌ضلعی دوضلعی مثلث چهارضلعی پنج‌ضلعی شش‌ضلعی هفت‌ضلعی هشت‌ضلعی نه‌ضلعی ده‌ضلعی
۱۱–۲۰ ضلعی	یازده‌ضلعی دوازده‌ضلعی سیزده‌ضلعی چهارده‌ضلعی پانزده‌ضلعی شانزده‌ضلعی هفده‌ضلعی هجده‌ضلعی نوزده‌ضلعی بیست‌ضلعی
موارد دیگر	سی‌ضلعی چهل‌ضلعی هزارضلعی میلیون‌ضلعی بی‌نهایت‌ضلعی
ستاره ضلعی	ستاره پنج‌پر ستاره شش‌پر ستاره هفت‌پر ستاره هشت‌پر ستاره نه‌پر ستاره ده‌پر ستاره یازده‌پر ستاره دوازده‌پر