مسئله کوچکترین دایره
مسئلهٔ کوچکترین دایره یا کمینه دایره پوششی نقاط، یک مسئله ریاضی است که کوچکترین دایره پوششی شامل همه نقاط صفحه اقلیدسی را محاسبه میکند. مسئله کوچکترین دایره پوششی در فضای n بعدی، مسئله ای است که کوچکترین کره که همه مجموعه نقاط را شامل میشود، محاسبه میکند.[1] این مسئله در ابتدا توسط ریاضیدان انگلیسی James Joseph Sylvester در سال ۱۸۵۷ مطرح شد.[2] مسئله کوچکترین دایره در صفحه یک مثال از مسئله تحلیل تعیین محل است به طوری که محل یک امکان جدید باید به گونهای انتخاب شود که دورترین فاصلهای که هر مشتری باید طی کند تا به این امکان برسد کمینه شود.[3]مسئله پیدا کردن کوچکترین دایره در صفحه در ابعاد بالاتر هم در زمان خطی قابل حل است.
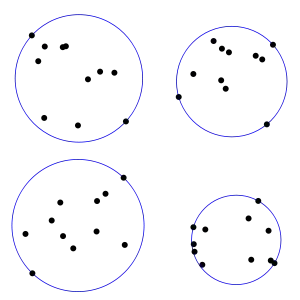
مشخصات
اغلب روشهای هندسی برای حل این مسئله، نقاطی را در نظر میگیرند که روی مرز کوچکترین دایره واقع شدهاند و برپایهٔ دو اصل سادهٔ زیر میباشند:
۱) کوچکترین دایرهٔ پوششی نقاط یکتاست.
۲) کوچکترین دایرهٔ پوششی برای مجموعهٔ نقاط S، حداکثر با ۳ نقطه از S روی مرز دایره مشخص میشود. اگر این دایره با دو نقطه مشخص شود، در این صورت خط متصل کنندهٔ این دو نقطه باید قطر کوچکترین دایرهٔ پوششی نقاط باشد و اگر با سه نقطه مشخص گردد آنگاه مثلث شامل این سه نقطه منفرجه نخواهد بود.
راه حلهای زمان خطی
همان طور که نیمورد مگیدو (Nimrod Megiddo) نشان داد،[4]مسئلهٔ کوچکترین دایره پوششی نقاط میتواند در زمان خطی حل شود و برای این مسئله در فضای اقلیدسی در هر بعد ثابتی همین زمان اجرا وجود دارد.
المو ولز(Emo Welzl)[5] یک الگوریتم تصادفی برای کوچکترین دایره پوششی نقاط با زمان اجرای (O(n ارائه داد که این الگوریتم بر پایهٔ الگوریتم برنامه خطی ریموند سیدل(Raimund Seidel) است. این الگوریتم بازگشتی، مجموعه نقاط Q و S را به عنوان آرگومان دریافت میکند و کوچکترین دایرهٔ پوششی از اجتماع Q و S را تا زمانی که هر نقطه از Q نقطهای از نقاط مرزی کوچکترین دایره نهایی شود محاسبه میکند. بنابراین، برای حل مسئله اصلی میتوانیم الگوریتم فوق را برای مجموعه S که شامل نقاطی که قرار است پوشش داده شوند و Q که یک مجموعه تهی است فراخوانی کرد. همانطور که الگوریتم به صورت بازگشتی فراخوانی میشود، مجموعه Q تا زمانی که مساوی همه نقاط مرزی دایره نشدهاست بزرگ میشود.
این الگوریتم نقاط درون مجموعه S و P را به صورت رندوم بررسی میکند و همچنین کوچکترین دایره شامل اجتماع P و Q را نیزمورد بررسی قرار میدهد. در هر مرحله، الگوریتم بررسی میکند که آیا نقطه بعدی r به این دایره تعلق دارد یا نه و اگر نداشت دایره را با دایرهٔ دیگری که از فراخوانی الگوریتم با آرگومانهای P و Q+r به دست میآید جایگزین میکند. چه دایره توسط دایره دیگری جایگزین شود و چه نشود، r جز مجموعه نقاط P محسوب میشود. در بررسی هر یک از نقاط، باید آزمایشهای مداومی انجام شود که مشخص کند آیا هر نقطه به یک دایره مستقل تعلق دارد و همچنین امکان اجرای یک الگوریتم بازگشتی را دارد یا نه. میتوان نشان داد که احتمال این که نقطه iام، یک الگوریتم بازگشتی تولید کند برابر با (O(۱/i است. به همین دلیل زمان کل اجرای مسئله خطی است.
متعاقباً، مسئله کوچکترین دایره جز کلاس عمومی مسئلههای نوع LP است که میتواند با استفاده از الگوریتمهایی چون ولز که مبتنی بر برنامهنویسی خطی هستند حل شود. در نتیجهٔ عضویت در این کلاس، نشان داده شد که اتکا به بُعد فاکتورهای ثابت در زمان محدود (O(n، که یک فاکتور برای تابعهای Seidel's است، میتواند به زیر مجموعههای نمایی که اتکا روی N را حفظ میکنند کاهش پیدا کند.[6]
سایر الگوریتمها
با توجه به بررسیهای مگیدو(Megiddo) و اینکه کوچکترین دایرهٔ پوششی میتواند با زمان اجرای خطی پیدا شود، تعداد زیادی از الگوریتمها با پیچیدگی بالاتر ظاهر شدند. سادهترین الگوریتم برای حل این مسئله از مرتبهٔ n۴ است به این ترتیب که تمام دایرههای متشکل از دو نقطه و سه نقطه ممکن را در نظر گرفته و سپس بین تمام آنها کمینه میگیرد.
- کریستال و پیرس(Chrystal and Peirce) الگوریتمی ارائه دادند که از استراتژی بهینهسازی محلی استفاده میکند به این ترتیب که دو نقطه روی مرز دایره در نظر میگیرد و با جایگزین کردن پی در پی جفت نقاط روی مرز، دایره را کوچک میکند تا به کمینهٔ خود برسد.
چاکرابرتی و چادهوری(Chakraborty and Chaudhuri)[7] یک روش خطی برای انتخاب دایرهٔ اولیهٔ مناسب و جفت نقاط روی مرز دایره ارائه کردهاند. با هر گام از این الگوریتم یکی از جفت نقاط روی مرز به عنوان یک راس جدید در پوش محدب قرار میگیرد؛ بنابراین اگر پوش حاوی h راس باشد، این الگوریتم میتواند در مرتبهٔ زمانی n*h پاسخ دهد.
- الزینگا و هرن(Elzinga and Hearn)[8] الگوریتمی را پیشنهاد دادند که یک دایرهٔ پوششی را برای زیر مجموعهای از نقاط نگه میدارد. در هر گام الگوریتم، از نقطهای که توسط حوزهٔ پوششی هنوز پوشش داده نشدهاست، برای پیدا کردن یک فضای پوششی بزرگ تر که زیر مجموعهٔ جدیدی از نقاط و البته شامل همین نقطه است، استفاده میشود. با اینکه این الگوریتم در بدترین حالت زمان اجرایی از مرتبهٔ h۳*n دارد، طراحان الگوریتم معتقدند که در آزمایشهایشان این الگوریتم در زمان خطی پاسخ میداده است. درنزر و شله(Drezner and Shelah) پیچیدگی این الگوریتم را بررسی کردهاند.[9]کد برنامه به دو زبان برنامهنویسی فورترن و ،C از هرن و ویجای و نیکل(Hearn, Vijay & Nickel) در دسترس هست.[10]
- مسئلهٔ کوچکترین حوزه میتواند به عنوان یک برنامه از درجهٔ دو[1] فرموله شود که با استفاده از یک سیستم محدودیت خطی و تابعهای محدب درجهٔ دو تعریف میشود. بنابراین هر الگوریتم جهت دار ممکن میتواند جواب مسئله را بدهد.[11]هرن و ویجای[12] ثابت کردند که راه حلهای ارائه شده از جکبسن و کریستال - پیرس معادل هم هستند.
- دوگان این برنامه درجهٔ دو ممکن است بتواند به صورت ضمنی فرمول بندی شود.[13] الگوریتمی از لاوسون[14] can be described in this way as a primal dual algorithm.[12]میتواند به عنوان یک راه حل دوگان اولیه محسوب شود.[12]
- شمُس وهای (Shamos and Hoey)[15] یک الگوریتم با زمان اجرای n*log n ارائه کردند بر این مبنا که مرکز کوچکترین دایرهٔ پوششی باید یک راس از دورترین نقطهٔ دیاگرام ورونوی از مجموعه نقاط ورودی باشد.
گونهٔ وزن دار مسئله
نسخهٔ وزن دار مسئلهٔ کوچکترین دایرهٔ پوششی، ورودیها را به عنوان مجموعهای از نقاط در فضای اقلیدسی در نظر میگیرد که هر کدام وزنی دارند. هدف این مسئله پیدا کردن نقطه ایست که بیشینه فاصلهٔ وزن دار با هر نقطهٔ دیگری را کمینه کند. مسئلهٔ اصلیِ کوچکترین دایرهٔ پوششی میتواند با اختصاص دادن همهٔ وزنها به همان اعداد بهبود پیدا کند. همانند نسخهٔ بدون وزن، حالت وزن دار مسئله میتواند در زمان خطی حل شود، بدیهی است که راه حلهایی با زمان اجرای کندتر نیز موجودند.[12][16][17]
منابع
- Elzinga, J.; Hearn, D. W. (1972), "The minimum covering sphere problem", Management Science, 19: 96–104, doi:10.1287/mnsc.19.1.96
- Sylvester, J. J. (1857), "A question in the geometry of situation", Quarterly Journal of Mathematics, 1: 79.
- Francis, R. L.; McGinnis, L. F.; White, J. A. (1992), Facility Layout and Location: An Analytical Approach (2nd ed.), Englewood Cliffs, N.J.: Prentice–Hall, Inc..
- Megiddo, Nimrod (1983), "Linear-time algorithms for linear programming in R3 and related problems", SIAM Journal on Computing, 12 (4): 759–776, doi:10.1137/0212052, MR 0721011.
- Welzl, Emo (1991), "Smallest enclosing disks (balls and ellipsoids)", in Maurer, H., New Results and New Trends in Computer Science, Lecture Notes in Computer Science, 555, Springer-Verlag, pp. 359–370, doi:10.1007/BFb0038202.
- Matoušek, Jiří; Sharir, Micha; Welzl, Emo (1996), "A subexponential bound for linear programming" (PDF), Algorithmica, 16: 498–516, doi:10.1007/BF01940877.
- Chakraborty, R. K.; Chaudhuri, P. K. (1981), "Note on geometrical solutions for some minimax location problems", Transportation Science, 15: 164–166, doi:10.1287/trsc.15.2.164.
- Elzinga, J.; Hearn, D. W. (1972), "Geometrical solutions for some minimax location problems", Transportation Science, 6: 379–394, doi:10.1287/trsc.6.4.379.
- Drezner, Z.; Shelah, S. (1987), "On the complexity of the Elzinga–Hearn algorithm for the 1-center problem", Mathematics of Operations Research, 12 (2): 255–261, JSTOR 3689688.
- Hearn, D. W.; Vijay, J.; Nickel, S. (1995), "Codes of geometrical algorithms for the (weighted) minimum circle problem", European Journal of Operational Research, 80: 236–237.
- Jacobsen, S. K. (1981), "An algorithm for the minimax Weber problem", European Journal of Operational Research, 6: 144–148, doi:10.1016/0377-2217(81)90200-9.
- Hearn, D. W.; Vijay, J. (1982), "Efficient algorithms for the (weighted) minimum circle problem", Operations Research, 30 (4): 777–795, doi:10.1287/opre.30.4.777.
- Elzinga, J.; Hearn, D. W.; Randolph, W. D. (1976), "Minimax multifacility location with Euclidean distances", Transportation Science, 10: 321–336, doi:10.1287/trsc.10.4.321.
- Lawson, C. L. (1965), "The smallest covering cone or sphere", SIAM Review, 7 (3): 415–417, doi:10.1137/1007084.
- Shamos, M. I.; Hoey, D. (1975), "Closest point problems", Proceedings of 16th Annual IEEE Symposium on Foundations of Computer Science, pp. 151–162, doi:10.1109/SFCS.1975.8.
- Megiddo, N. (1983), "The weighted Euclidean 1-center problem", Mathematics of Operations Research, 8: 498–504, doi:10.1287/moor.8.4.498.
- Megiddo, N.; Zemel, E. (1986), "An O(n log n) randomizing algorithm for the weighted Euclidean 1-center problem", Journal of Algorithms, 7: 358–368, doi:10.1016/0196-6774(86)90027-1.
پیوند به بیرون
- Bernd Gärtner's smallest enclosing ball code
- CGAL the Min_sphere_of_spheres package of the Computational Geometry Algorithms Library (CGAL)
- Miniball an open-source implementation of an algorithm for the smallest enclosing ball problem for low and moderately high dimensions
