زاویه محاطی

زاویهٔ محاطی در هندسه هنگامی ساخته می‌شود که دو خط گذرا از روی دایره (یا در تباهیدگی یک خط قطع کننده و یک خط مماس) با یکدیگر روی پیرامون دایره برخورد کنند.

به بیان ساده‌تر اگر یک زاویه درون یک دایره باشد و ضلع‌های زاویه، دو وتر از دایره باشد که با هم یک نقطهٔ مشترک دارند، چنین زاویه‌ای زاویهٔ محاطی نام دارد. در کتاب سوم اصول اقلیدس، گزاره‌های ۲۰ تا ۲۲، ویژگی‌های این زاویه گفته شده‌است. اگر یک زاویهٔ مرکزی و یک زاویهٔ محاطی هر دو یک کمان از دایره را دربرداشته باشند، اندازهٔ زاویهٔ محاطی نصف زاویهٔ مرکزی خواهد بود.

اثبات

زاویهٔ محاطی با یک قطر

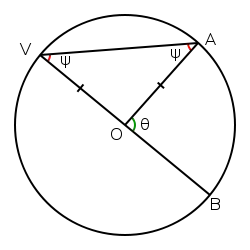
اگر O مرکز دایره باشد، دو نقطهٔ بر روی محیط دایره انتخاب کنید و آن‌ها را به ترتیب V و A بنامید. V را به O وصل کنید و آن را ادامه دهید تا با پیرامون دایره در نقطهٔ B برخورد کند. چون این خط از مرکز دایره گذشته‌است پس قطر دایره‌است در نتیجه V در یک سوی قطر و B در سوی دیگر آن جای گرفته‌است. حال زاویه‌ای بکشید که راس آن در نقطهٔ V باشد و دو لبهٔ آن از A و B بگذرد.

نقطهٔ A را به O وصل کنید. زاویهٔ BOA یک زاویهٔ مرکزی است. آن را θ بنامید. دو پاره خط OA و OV با هم برابرند چون هر دو شعاع دایره‌اند. پس مثلث VOA متساوی‌الساقین است. در نتیجه دو زاویهٔ BVA (زاویهٔ محاطی) و VAO با هم برابرند. هر دوی این زاویه‌ها را ψ می‌نامیم.

زاویه‌های BOA و AOV با هم مکمل اند و مجموع آن‌ها ۱۸۰ درجه می‌شود. چون خط VB از O می‌گذرد و یک خط راست است پس اندازهٔ زاویهٔ AOV از رابطهٔ ۱۸۰° − θ بدست می‌آید.

از سوی دیگر می‌دانیم که مجموع زاویه‌های داخلی مثلث ۱۸۰ درجه‌است. سه زاویهٔ داخلی مثلث VOA عبارتند از: ۱۸۰° − θ و ψ ،ψ. بنابراین:

${\displaystyle 2\psi +180^{\circ }-\theta =180^{\circ }.}$

۱۸۰° را از دو سوی تساوی کم می کنیم.

${\displaystyle 2\psi =\theta ,\,}$

که در آن θ زاویهٔ مرکزی کمان AB است و ψ زاویهٔ محاطی همان کمان است که اندازه‌ای برابر با نصف آن دارد.

زاویهٔ محاطی و مرکز دایره درون آن

دایره‌ای با مرکز O را در نظر بگیرید. سه نقطهٔ V, C و D را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.

کمان DC نقطهٔ E را در بر می‌گیرد و می‌دانیم که این نقطه بر روی قطری از دایره قرار دارد. از سوی دیگر زاویه‌های DVE و EVC هر دو زاویهٔ محاطی‌اند. در بخش پیشین بدست آوردیم که اگر یک ضلع زاویهٔ محاطی از مرکز دایره بگذرد اندازهٔ آن برابر نصف کمان روبروی آن است. حال از داده‌های بخش پیشین بهره می‌گیریم:

${\displaystyle \angle DVC=\angle DVE+\angle EVC.\,}$

پس داریم:

${\displaystyle \psi _{0}=\angle DVC,}$

${\displaystyle \psi _{1}=\angle DVE,}$

${\displaystyle \psi _{2}=\angle EVC,}$

نتیجه می‌گیریم:

${\displaystyle \psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)}$

حال خط‌های OC و OD را می‌کشیم. زاویهٔ DOC یک زاویهٔ مرکزی است. همچنین زاویه‌های DOE و EOC هم زاویه‌های مرکزی‌اند؛ و می‌دانیم:

${\displaystyle \angle DOC=\angle DOE+\angle EOC.}$

اگر فرض کنیم:

${\displaystyle \theta _{0}=\angle DOC,}$

${\displaystyle \theta _{1}=\angle DOE,}$

${\displaystyle \theta _{2}=\angle EOC,}$

آنگاه:

${\displaystyle \theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)}$

پیشتر از بخش یک می‌دانیم که ${\displaystyle \theta _{1}=2\psi _{1}}$ و ${\displaystyle \theta _{2}=2\psi _{2}}$ با توجه به تمامی این داده‌ها و معادلهٔ (۲) بدست می‌آوریم که:

${\displaystyle \theta _{0}=2\psi _{1}+2\psi _{2}\,}$

با توجه به رابطهٔ (۱) خواهیم داشت:

${\displaystyle \theta _{0}=2\psi _{0}.\,}$

زاویهٔ محاطی که مرکز دایره در بیرون آن جای دارد

دایره‌ای با مرکز O را در نظر بگیرید. سه نقطهٔ V, C و D را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.

می‌دانیم که نقطهٔ E که بر روی قطری از دایره جای دارد. همچنین می‌دانیم که زاویه‌های DVE و EVC هم زاویه‌هایی محاطی‌اند. در بخش‌های پیشین نشان دادیم که اندازهٔ زاویهٔ محاطی که ضلعش از روی مرکز دایره بگذرد برابر نصف کمان روبرویش است. پس خواهیم داشت:

${\displaystyle \angle DVC=\angle EVC-\angle DVE}$.

اگر فرض کنیم:

${\displaystyle \psi _{0}=\angle DVC,}$

${\displaystyle \psi _{1}=\angle DVE,}$

${\displaystyle \psi _{2}=\angle EVC,}$

آنگاه

${\displaystyle \psi _{0}=\psi _{2}-\psi _{1}\qquad \qquad (3)}$

خط‌های OC و OD را بکشید. زاویهٔ DOC یک زاویهٔ مرکزی است همچنین می‌دانیم که زاویه‌های DOE و EOC هم زاویه‌هایی مرکزی‌اند. با توجه به آنکه

${\displaystyle \angle DOC=\angle EOC-\angle DOE.}$

اگر فرض کنیم

${\displaystyle \theta _{0}=\angle DOC,}$

${\displaystyle \theta _{1}=\angle DOE,}$

${\displaystyle \theta _{2}=\angle EOC,}$

آنگاه خواهیم داشت:

${\displaystyle \theta _{0}=\theta _{2}-\theta _{1}\qquad \qquad (4)}$

با توجه به نکته‌هایی که در بخش یک گفته شد می‌دانیم که ${\displaystyle \theta _{1}=2\psi _{1}}$ و ${\displaystyle \theta _{2}=2\psi _{2}}$ است. با توجه به این تساوی‌ها و رابطهٔ (۴):

${\displaystyle \theta _{0}=2\psi _{2}-2\psi _{1}}$

پس، از رابطهٔ (۳) خواهیم داشت:

${\displaystyle \theta _{0}=2\psi _{0}.}$

منابع

• ویکی‌پدیای انگلیسی

• Ogilvy CS (1990). Excursions in Geometry. Dover. pp. 17&ndash, 23. ISBN 0-486-26530-7.
• Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. pp. ۱۷۲. ISBN 0-442-22646-2.

پیوند به بیرون

• زاویهٔ محاطی در پایگاه مجازی مث‌ورلد.
• رابطهٔ میان زاویه‌های مرکزی و محاطی
• خوراک زاویهٔ محاطی در وبگاه cut-the-knot
• زاویه مرکزی همراه با پویانمایی
• زاویهٔ محاطی همراه با پویانمایی
• قضیهٔ زاویهٔ مرکزی همراه با پویانمایی