وتر دایره

وتر یک دایره پاره‌خط راستی است که هر دو انتهای آن روی محیط دایره قرار دارند. یک خط قاطع، امتداد نامتناهی یک وتر دایره است. با تعمیم، وتر به معنای پاره‌خطی که دو نقطه روی هر منحنی‌ای (مثلاً بیضی) را به هم متصل می‌کند. وتری که از مرکز یک دایره بگذرد، یک قطر آن دایره است.

پاره‌خط سرخ BX یک وتر
این دایره را مشخص می‌کند. (قطر AB هم یک وتر حساب می‌شود).

مثلثات
تاریخ کاربرد توابع (توابع معکوس) مثلثات تعمیم‌یافته مطالعه بیشتر
منابع
اتحادها مقدارهای دقیق جدول‌ها دایره واحد
قوانین و قضایا
قانون سینوس‌ها قانون کسینوس‌ها قانون تانژانت‌ها قانون کتانژانت‌ها قضیه فیثاغورس
حساب دیفرانسیل و انتگرال
جانشینی مثلثاتی انتگرال توابع (انتگرال توابع وارون) مشتق توابع

ویژگی‌های وتر یک دایره

تعدادی از ویژگی‌های مربوط به دایره به شرح زیر هستند:

1. همهٔ وترهای هم‌فاصله از مرکز دایره، هم‌اندازه هستند.
2. وتری که از مرکز دایره بگذرد دارای طول بیشینه است و قطر نامیده می‌شود.
3. اگر امتداد (خطوط قاطع) دو وتر AB و CD در نقطه P به هم برسند، آن‌گاه رابطه AP·PB = CP·PD در مورد طول پاره‌خط‌ها برقرار خواهد بود. (مقدار AP·PB قوت نقطه P نسبت به این دایره است).

مساحتی که یک وتر از دایره جدا می‌کند یک قطعه دایره نام دارد.

وترهای یک بیضی

نقطه‌های میانی تعدادی از وترهای موازی یک بیضی هم‌خط هستند.

وترهای دایره و مثلثات

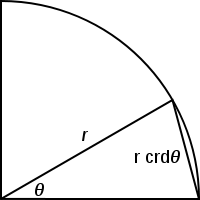
وترهای به‌طور گسترده‌ای در مراحل ابتدایی مثلثات مورد استفاده بودند. در نخستین جدول مثلثاتی شناخته‌شده که هیپارخوس آن را گردآوری کرده، مقادیر تابع وتر برای هر ۷٫۵ درجه مشخص شده‌است. در قرن دوم میلادی بطلمیوس اسکندرانی جدول جامع‌تری از مقادیر تابع وتر در کتاب خود در نجوم ارائه کرد. در جدول بطلمیوس، مقدار وتر هر زاویه‌ای در بازه ۱/۲ درجه تا ۱۸۰ درجه با فواصل یک و نیم درجه‌ای آمده‌است. بطلمیوس به جای دایره واحد از دایره‌ای به قطر ۱۲۰ استفاده کرده و دقت مقادیر تابع وتر هم تا رقم دوم مبنای ۶۰ (ثانیه) بعد از اعشار است.

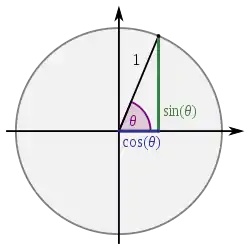
تعریف هندسی تابع وتر در تصویر نشان داده شده‌است. مقدار وتر یک زاویه، طول وتری است که این زاویه از دایره واحد جدا می‌کند. تابع وتر را می‌توان با کمک قضیه فیثاغورس به تابع مثلثاتی مدرن سینوس مرتبط کرد. کافی است نقطه‌های (۰، ۱) و (cos θ, sin θ) را در نظر گرفته و فاصله آن‌ها را حساب کنیم تا طول وتر مورد نظر را به دست آوریم:

${\displaystyle \mathrm {crd} \ \theta ={\sqrt {(1-\cos \theta )^{2}+\sin ^{2}\theta }}={\sqrt {2-2\cos \theta }}=2\sin \left({\frac {\theta }{2}}\right)}$

در آخرین مرحله از اتحاد زاویه دو برابر استفاده شده‌است. همان‌طور که مثلثات مدرن بر مبنای تابع سینوس بنا شده‌است، مثلثات عهد باستان هم بر اساس تابع وتر ساخته شده بود. هیپارخوس مدعی است که کتابی دوازده جلدی دربارهٔ وترها نوشته‌است اما این اثر هم‌اکنون در دسترس نیست. ادعای هیپارخوس نشان می‌دهد که او احتمالاً بسیاری از ویژگی‌های وترها را می‌شناخته‌است. اتحادهایی شبیه اتحادهای مثلثاتی مدرن برای تابع وتر وجود دارد:

نام اتحاد	شکل مدرن اتحاد	اتحاد مشابه با استفاده از تابع وتر
فیثاغورس	${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1\,}$	${\displaystyle \mathrm {crd} ^{2}\theta +\mathrm {crd} ^{2}(180^{\circ }-\theta )=4\,}$
زاویه دوبرابر	${\displaystyle \sin {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{2}}}\,}$	${\displaystyle \mathrm {crd} \ {\frac {\theta }{2}}=\pm {\sqrt {2-\mathrm {crd} (180^{\circ }-\theta )}}\,}$
ارتفاع چندضلعی بر اساس زاویه	${\displaystyle c=2r\sin \left({\frac {\theta }{2}}\right)}$	${\displaystyle c={\frac {D}{2}}\mathrm {crd} \ \theta }$

هم‌چنین، معکوس تابع وتر هم بر اساس معکوس تابع سینوس قابل بیان است:[1]

${\displaystyle \operatorname {acrd} (y)=2\arcsin \left({\frac {y}{2}}\right)\,}$

جستارهای وابسته

• قطعه دایره - مساحتی که وتر از دایره جدا می‌کند
• بطلمیوس
• قضیه هلدیچ دربارهٔ چرخش یک وتر در یک منحنی محدب بسته
• گراف دایره
• اگزوسکانت و اگزوکسکانت (نسبت مثلثاتی باستانی)
• ورساین و هاورساین (نسبت مثلثاتی باستانی)

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Chord (geometry)». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۴ اوت ۲۰۱۶.

1. «سورس‌کد فرترن ۹۰ تابع معکوس وتر». مرکز پروازهای فضایی گودارد ناسا. ۸ نوامبر ۲۰۰۱. دریافت‌شده در ۴ اوت ۲۰۱۶.

پیوند به بیرون

• تاریخچه مثلثات (انگلیسی)
• توابع مثلثاتی, با تمرکز بر تاریخچه (انگلیسی)
• وتر (یک دایره) با انیمیشن‌های تعاملی (انگلیسی)