قضیه تالس (دایره)

قضیه تالس در هندسه این مطلب را بیان می‌کند که اگر A و B و C نقاط روی دایره باشند و خط AC قطر دایره باشد، آن وقت زاویه ABC یک زاویهٔ قائمه خواهد بود. به بیان دیگر مرکز دایره محیطی مثلث روی یکی از اضلاع مثلث قرار می‌گیرد، اگر و تنها اگر آن مثلث قائم‌الزاویه باشد.

تاریخچه

تالس اولین کسی نبود که این قضیه را کشف کرد. قبل از او مصریان و بابلیان این قضیه را می‌دانستند، ولی آنها نتوانسته بودند اثباتی برای آن پیدا کنند. چون این قضیه اولین بار توسط تالس اثبات شد، به نام او نیز معروف شد.

اثبات

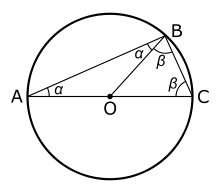
اثبات قضیهٔ تالس

فرض کنیم ${\displaystyle O}$ مرکز دایره باشد. آنگاه ${\displaystyle OA=OB=OC}$ و ${\displaystyle \vartriangle OAB}$ و ${\displaystyle \vartriangle OBC}$ متساوی‌الساقین خواهند بود. در نتیجه ${\displaystyle {\widehat {BAO}}={\widehat {ABO}}}$ و ${\displaystyle {\widehat {OCB}}={\widehat {OBC}}}$.

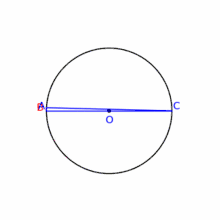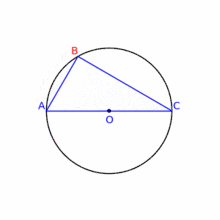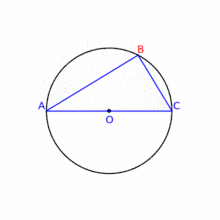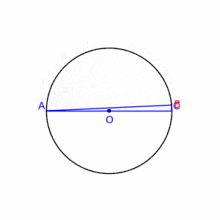
با جابجایی نقطهٔ B روی محیط دایره زاویهٔ B تغییری نمی‌کند و ۹۰ درجه می‌ماند

فرض کنیم ${\displaystyle \alpha ={\widehat {ABO}}}$ و ${\displaystyle \beta ={\widehat {OCB}}}$. چون جمع زوایای داخلی مثلث برابر ۱۸۰ درجه‌است پس:

${\displaystyle {\widehat {OCB}}+{\widehat {ABC}}+{\widehat {BAO}}=2\alpha +2\beta =180^{\circ }\Rightarrow \alpha +\beta =90^{\circ }}$

${\displaystyle {\widehat {ABC}}=\alpha +\beta =90^{\circ }}$

منابع

قضیه تالس | دانشنامهٔ رشد

پیوند به بیرون

اثبات قضیه تالس