ماتریس تصادفی
در ریاضیات یک ماتریس تصادفی (ماتریس احتمال، ماتریس انتقال،[1] ماتریس جایگزینی یا ماتریس مارکوف هم نامیده میشود) ماتریس مورد استفاده برای توصیف انتقالهای یک زنجیره مارکوف است. هر یک از درایههای این ماتریس عدد حقیقی غیرمنفی است که احتمال را نشان میدهد. این ماتریس در نظریه احتمال ،آمار، ریاضی مالی و جبر خطی و همچنین علوم کامپیوتر و ژنتیک جمعیت کاربرد دارد. تعاریف متعددی و انواع ماتریس تصادفی:
- یک ماتریس تصادفی راست یک ماتریس مربعی حقیقی است که جمع هر سطرش میباشد.
- یک ماتریس تصادفی چپ یک ماتریس مربعی حقیقی است که جمع هر ستونش میباشد.
- یک ماتریس تصادفی دوگانه یک ماتریس مربعی از اعداد حقیقی غیر منفی است که جمع هر سطر و ستونش میباشد.
به همین شیوه میتوان بردار تصادفی (بردار احتمال نیز نامیده میشود) را تعریف کرد؛ که برداری است با مقادیر حقیقی غیرمنفی و مجموع . بنابراین هر سطر از ماتریس تصادفی راست (یا ستون از ماتریس تصادفی چپ) یک بردار تصادفی است.
قرارداد رایج در ادبیات ریاضی دانان انگلیسی زبان این است که از بردار سطری ماتریس تصادفی راست و احتمالات استفاده کنند تا بردار ستونی ماتریس تصادفی چپ و احتمالات؛ در این مقاله از این قرارداد رایج استفاده شدهاست.
تعریف و ویژگیها
یک ماتریس تصادفی زنجیره مارکوف با تعداد حالات محدود از فضای را توصیف میکند.
اگر احتمال حرکت از حالت به حالت در یک مرحله زمانی را با عبارت ماتریس تصادفی با استفاده از با عنصر ردیف و ستون مشخص خواهد شد،
با توجه به اینکه مجموع احتمال گذار از حالت به تمام حالات دیگر باید باشد، این ماتریس یک ماتریس تصادفی راست، پس
حاصل ضرب دو ماتریس تصادفی راست نیز یک ماتریس تصادفی راست است. به ویژه توان ماتریس تصادفی راست ، نیز یک ماتریس تصادفی راست است. احتمال انتقال از حالت به حالت در دو گام با عنصر از مربع ماتریس :
در کل احتمال انتقال رفتن از هر حالت به حالت دیگر در زنجیره مارکوف با ماتریس و در k مرحله با ماتریس .
توزیع اولیه با بردار سطری نمایش داده میشود.
بردار احتمال مانا که به عنوان یک توزیع تعریف میشود، به صورت یک بردار سطری نوشته میشود، که با اعمال ماتریس انتقال تغییر نمیکند؛ به عبارت دیگر، این بردار به صورت توزیع احتمال روی مجموعه تعریف میشود. این بردار، بردار ویژه ماتریس احتمال متناظر با مقدار ویژه میباشد:
شعاع طیفی راست هر ماتریس تصادفی راست حداکثر میباشد. علاوه بر این، هر ماتریس تصادفی راست یک بردار ویژه ستونی بدیهی متناظر با مقدار ویژه دارد: بردار میباشند. همانطور که مقادیر ویژه چپ و راست یک ماتریس مربعی یکسان هستند، هر ماتریس تصادفی، حداقل یک بردار ویژه سطری متناظر با مقدار ویژه دارد و اندازه مطلق بزرگترین مقادیر ویژهاش است. در نهایت طبق قضیه مقدار ثابت براوئر (اعمال شده به مجموعه محدب فشرده از تمام توزیعهای احتمال مجموعه متناهی ) حاکی از آن است که بردارهای ویژه چپی هم وجود دارند که بردار احتمال مانا باشند.
از سوی دیگر قضیه پرون-فربنیوس تضمین میکند که هر ماتریس تصادفی کاهش ناپذیر چنین بردار مانایی دارد و اندازه مطلق بزرگترین مقدار ویژه اش همیشه است. این قضیه را نمیتوان بهطور مستقیم به این ماتریسها اعمال کرد، زیرا لازم نیست کاهش ناپذیر باشند.
بهطور کلی ممکن است چندین بردار مانا وجود داشته باشند. هرچند، برای ماتریس با مقادیر مثبت آرایه (یا بهطور کلی تر برای ماتریس تصادفی کاهش ناپذیر غیرپریودیک) این بردار منحصر به فرد است و با استفاده از حد زیر میتوان آن را بدست آورد:
که عنصر از بردار سطری . به بیان دیگر در دراز مدت، احتمال بودن در حالت مستقل از حالت اولیه . نتیجه هر دوی این محاسبات بردار مانای یکسانی خواهد بود و این نتیجه از نظریه ارگودیک است، که به صورت عمومی در طیف گستردهای از سیستمهای دینامیکی اتلافی درست است: سیستم در طول زمان به یک حالت ایستا تکامل مییابد.
بهطور شهودی، یک ماتریس تصادفی، نشان دهنده یک زنجیره مارکوف است؛ با اعمال ماتریس تصادفی به توزیع احتمال، جرم احتمال توزیع اولیه را با حفظ جرم کلی مجدداً توزیع میکند. اگر این روال برای زنجیره مارکوف به صورت مداوم تکرار شود، توزیع به توزیع مانا همگرا خواهد شود.
مثال: گربه و موش
فرض کنید شما یک تایمر و یک ردیف از پنج جعبه مجاور دارید؛ در زمان صفر یک گربه در جعبه اول و یک موش در جعبه پنجم قرار گرفتهاند. با جلو رفتن زمان تایمر، گربه و موش هر دو به صورت تصادفی پرشی به یکی از جعبههای مجاورشان خواهند داشت. برای مثال اگر گربه در جعبه دوم و موش در جعبه چهارم باشد، احتمال اینکه با گذر یک مرحله از زمان تایمر، گربه در جعبه اول و موش در جعبه پنجم قرار گیرد یک چهارم است. اگر گربه در جعبه اول و موش در جعبه پنجم باشد، با احتمال با گذر یک مرحله از زمان، گربه در جعبه دو و موش در جعبه چهار خواهد بود. اگر گربه و موش به داخل جعبه یکسانی پرش داشته باشند، گربه موش را میخورد و بازی تمام خواهد شد. متغیر تصادفی نشان دهند تعداد مراحل زمانی است که موش در بازی زنده خواهند ماند.
زنجیره مارکوفی این بازی حالت دارد که هر حالت نشان دهنده موقعیت گربه و موش در بازی است. توجه داشته باشید گرچه شمارش عادی تعداد حالات خواهد بود، اما تعدادی از آنها حالات غیرممکن هستند: چون موش نمیتواند شماره کوچکتری از شماره گربه داشته باشد (که معنی ماوس را اشغال گربه جعبه و جان سالم به در برد به گذشته حرکت میکند) یا اینکه مجموع دو شماره آنها باید همیشه زوج باشد. ضمناً حالت منجر به مرگ مو خواهند شد و این سه حالت را ترکیب کرده و یک حالت در نظر میگیریم:
- حالت :
- حالت :
- حالت :
- حالت :
- حالت : انتهای بازی: ، و .
برای نمایش احتمال انتقال این سیستم از ماتریس تصادفی استفاده میکنیم (سطرها و ستونهای این ماتریس با شماره حالات ممکن ذکر شده در بالا شماره گذاری شدهاند. حالت قبل از انتقال به صورت ردیف و حالت پس از انتقال به صورت ستون در نظر گرفته میشود).
میانگینهای دراز مدت
حالت اولیه گربه هر حالتی که باشد، در نهایت گربه موش را میگیرد (با احتمال ) و یک حالت مانای پیشنهادی است. برای محاسبه میانگین دراز مدت یا امید متغیر تصادفی ، برای هر حالت و زمان سهم وجود دارد. بقا را میتوان با یک متغیر باینری با برای حالت بقا و برای حالت اختتام نشان داد. حالتهای با در میانگین دراز مدت دخیل نیستند.
نمایش فاز-نوع
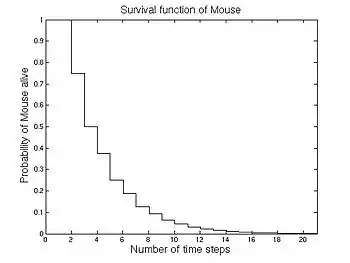
حالت یک حالت جذب است، توزیع زمان جذب، توزیع فاز-نوع گسسته است. فرض کنید سیستم با حالت شروع شود که آن را با بردار نشان میدهیم. حالاتی که در آنها موش میمیرد، در میانگین بقا تأثیری نخواهند داشت و میتوان حالت را نادیده گرفت. حالت اولیه و ماتریس انتقال را میتوان به صورت زیر کاهش داد:
و
که در آن ماتریس همانی و بردار ستونی تماماً ۱ میباشد (نقش جمعکننده روی حالات را دارد).
از آن جایی که هر حالت فقط برای یک مرحله زمانی اشغال خواهد شد، زمان مورد انتظار بقای موش جمع احتمال اشغال روی تمام حالات بقا و مراحل زمانی است.
ممانهای مرتبه بالاتر با عبارت زیر تعیین میشوند
جستارهای وابسته
- نامساوی مویرهد
- قضیه پرون-فربنیوس
- ماتریس چگالی
- ماتریس تصادفی دوگانه
- توزیع فاز-نوع گسسته
- اتوماتای احتمالاتی
- مدلهای سیر تکاملی دیانای
- کرنل مارکوف هم ارز ماتریس تصادفی در فضای حالت پیوسته
منابع
- Asmussen, S. R. (2003). "Markov Chains". Applied Probability and Queues. Stochastic Modelling and Applied Probability. 51. pp. 3–8. doi:10.1007/0-387-21525-5_1. ISBN 978-0-387-00211-8.
- G. Latouche, V. Ramaswami. Introduction to Matrix Analytic Methods in Stochastic Modeling, 1st edition. Chapter 2: PH Distributions; ASA SIAM, 1999.