تابع هذلولوی

توابع هُذلولوی، هُذلولی، یاتوابع هیپربولیک (به فرانسوی: hyperbolique)، از توابع پرکاربرد در ریاضیات می‌باشند که روابط حاکم بر آنها شبیه مثلثات است، با این تفاوت که خطوط مثلثاتی با توجه به دایره‌ای که شعاع آن واحد می‌باشد تعریف می‌شوند، ولی توابع هذلولوی (هذلولی) با توجه به هذلولی متساوی‌الساقین تعریف می‌گردند. از تابع‌های پایه‌ای آن sinh (خوانده می‌شود: سینوس هذلولوی یا هیپربولیک) و cosh (کسینوس هذلولوی) هستند که دیگر توابع را مانند tanh (تانژانت هذلولوی) می‌سازند. این توابع در انتگرالها، معادلات دیفرانسیل خطی و همچنین معادله لاپلاس بسیار ظاهر می‌شوند. همانند توابع مثلثاتی که دارای معکوس‌اند، این توابع نیز دارای معکوس‌اند و با پیش‌وندهای arc نمایش داده می‌شوند. مانند: arcsinh

در تعریف این توابع، منحنی سمت راست هذلولی متساوی‌الساقین را در نظر می‌گیریم که در این صورت داریم: x = cosh a و y = sinh a و در یک رابطه کلی خواهیم داشت:${\displaystyle \cosh ^{2}x-\sinh ^{2}x=1}$

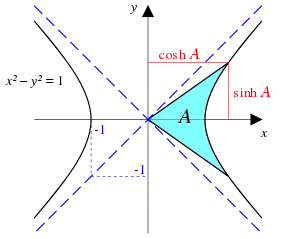
تابع‌های هیپربولیک برای توصیف حرکت موج در اجسام کشسان، شکل خطوط انتقال نیروی برق، توزیع دما در پره‌های فلزی که لوله‌های داغ را سرد می‌کنند، خم‌های تعقیب و هندسهٔ نظریهٔ نسبیت عام به کار می‌روند.

تعاریف

توابع هایپربولیک از این قراراند:

sinh, cosh و tanh

csch, sech and coth

${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}$

${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}$

${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {\frac {e^{x}-e^{-x}}{2}}{\frac {e^{x}+e^{-x}}{2}}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}$

${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {\frac {e^{x}+e^{-x}}{2}}{\frac {e^{x}-e^{-x}}{2}}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}$

${\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}}$

${\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}}$

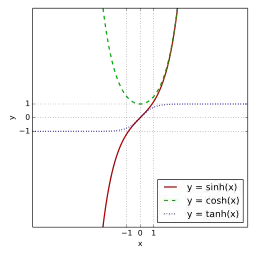
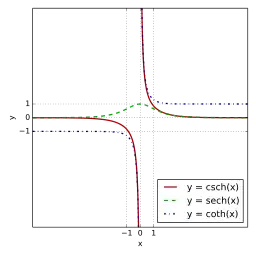
رابطهٔ توابع هایپربولیک با توابع مثلثلتی چنین است:

${\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}$

${\displaystyle \cosh x=\cos {\rm {i}}x\!}$

${\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}$

${\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}$

${\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}$

${\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}$

که در آن i یکهٔ موهومی با تعریف i^۲ = −۱ است.

روابط مفید

${\displaystyle coshx}$ و ${\displaystyle sechx}$ توابعی زوج و بقیه فرد هستند:

${\displaystyle {\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\\\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\operatorname {csch} (-x)&=-\operatorname {csch} x\end{aligned}}}$

همچنین داریم:

${\displaystyle {\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} {\frac {1}{x}}\\\operatorname {arcsch} x&=\operatorname {arsinh} {\frac {1}{x}}\\\operatorname {arcoth} x&=\operatorname {artanh} {\frac {1}{x}}\end{aligned}}}$

متناظر با روابط مثلثاتی داریم:

${\textstyle {\begin{aligned}\cosh ^{2}x-\sinh ^{2}x=1\\\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x-1\\\end{aligned}}}$

مجموع دو عبارت:

${\displaystyle {\begin{aligned}\cosh(x+y)&=\sinh x\sinh y+\cosh x\cosh y\\\sinh(x+y)&=\cosh x\sinh y+\sinh x\cosh y\end{aligned}}}$

مشخصاً

${\displaystyle {\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\end{aligned}}}$

مجموع و تفاضل ${\displaystyle coshx}$ و ${\displaystyle sinhx}$

${\displaystyle {\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\end{aligned}}}$

معکوس توابع

${\displaystyle arcsinhx=\sinh ^{-1}x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}$

${\displaystyle arccoshx=\cosh ^{-1}x=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1}$

${\displaystyle arctanhx=\tanh ^{-1}x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right);\left|x\right|<1}$

مشتق‌ها

${\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}$

${\displaystyle {\frac {d}{dx}}\cosh x=\sinh x\,}$

${\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x=\operatorname {sech} ^{2}x=1/\cosh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-1/\sinh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\ \operatorname {csch} \,x=-\coth x\ \operatorname {csch} \,x\,}$

${\displaystyle {\frac {d}{dx}}\ \operatorname {sech} \,x=-\tanh x\ \operatorname {sech} \,x\,}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}$

انتگرال‌های استاندارد

برای فهرست کاملی از این انتگرالها، فهرست انتگرال‌های تابع‌های هیپربولیک را ببینید.

${\displaystyle {\begin{aligned}\int \sinh(ax)\,dx&=a^{-1}\cosh(ax)+C\\\int \cosh(ax)\,dx&=a^{-1}\sinh(ax)+C\\\int \tanh(ax)\,dx&=a^{-1}\ln(\cosh(ax))+C\\\int \coth(ax)\,dx&=a^{-1}\ln(\sinh(ax))+C\\\int \operatorname {sech} (ax)\,dx&=a^{-1}\arctan(\sinh(ax))+C\\\int \operatorname {csch} (ax)\,dx&=a^{-1}\ln \left(\tanh \left({\frac {ax}{2}}\right)\right)+C\end{aligned}}}$

${\displaystyle {\begin{aligned}\int {\frac {du}{\sqrt {a^{2}+u^{2}}}}&=\sinh ^{-1}\left({\frac {u}{a}}\right)+C\\\int {\frac {du}{\sqrt {u^{2}-a^{2}}}}&=\cosh ^{-1}\left({\frac {u}{a}}\right)+C\\\int {\frac {du}{a^{2}-u^{2}}}&=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}\\\int {\frac {du}{a^{2}-u^{2}}}&=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}\\\int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}&=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C\\\int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}&=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C\end{aligned}}}$

پیوند به بیرون

• معکوس توابع هیپربولیک

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Hyperbolic function». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۹ شهریور ۱۳۹۰.

در ویکی‌انبار پرونده‌هایی دربارهٔ تابع هذلولوی موجود است.