شبکه عصبی پیچشی
شبکههای عصبی پیچشی یا همگشتی (به انگلیسی: convolutional neural network) (مخفف انگلیسی: CNN یا ConvNet) ردهای از شبکههای عصبی ژرف هستند که معمولاً برای انجام تحلیلهای تصویری یا گفتاری در یادگیری ماشین استفاده میشوند.
| یادگیری ماشین و دادهکاوی |
|---|
 |
شبکههای عصبی پیچشی به منظور کمینه کردن پیشپردازشها از گونهای از پرسپترونهای چندلایه استفاده میکنند.[1] به جای شبکه عصبی پیچشی گاهی از این شبکهها با نام شبکههای عصبی تغییرناپذیر با انتقال (shift invariant) یا تغییرناپذیر با فضا (space invariant) هم یاد میشود. این نامگذاری بر مبنای ساختار این شبکه است که در ادامه به آن اشاره خواهیم کرد.[2][3]
ساختار شبکههای پیچشی از فرایندهای زیستی قشر بینایی گربه الهام گرفتهشدهاست. این ساختار به گونهای است که تکنورونها تنها در یک ناحیه محدود به تحریک پاسخ میدهند که به آن ناحیه پذیرش گفته میشود.[4] نواحی پذیرش نورونهای مختلف به صورت جزئی با هم همپوشانی دارند به گونه ای که کل میدان دید را پوشش میدهند.
شبکههای عصبی پیچشی نسبت به بقیه رویکردهای دستهبندی تصاویر به میزان کمتری از پیشپردازش استفاده میکنند. این امر به معنی آن است که شبکه معیارهایی را فرامیگیرد که در رویکردهای قبلی به صورت دستی فراگرفته میشدند. این استقلال از دانش پیشین و دستکاریهای انسانی در شبکههای عصبی پیچشی یک مزیت اساسی است.
تا کنون کاربردهای مختلفی برای شبکههای عصبی از جمله در بینایی کامپیوتر، سیستمهای پیشنهاددهنده و پردازش زبان طبیعی پیشنهاد شدهاند.[5]
طراحی
یک شبکه عصبی پیچشی از یک لایه ورودی، یک لایه خروجی و تعدادی لایه پنهان تشکیل شدهاست. لایههای پنهان یا پیچشی هستند، یا تجمعی یا کامل.
لایههای پیچشی
لایههای پیچشی یک عمل پیچش را روی ورودی اعمال میکنند، سپس نتیجه را به لایه بعدی میدهند. این پیچش در واقع پاسخ یک تکنورون را به یک تحریک دیداری شبیهسازی میکند.[6]
هر نورون پیچشی دادهها را تنها برای ناحیه پذیرش خودش پردازش میکند. مشبککردن به شبکههای پیچشی این اجازه را میدهد که انتقال، دوران یا اعوجاج ورودی را تصحیح کنند.
اگرچه شبکههای عصبی پیشخور کاملاً همبند میتوانند برای یادگیری ویژگیها و طبقهبندی داده به کار روند، این معماری در کاربرد برای تصاویر به کار نمیرود. در این حالت حتی برای یک شبکه کمعمق تعداد بسیار زیادی نورون لازم است. عمل پیچش یک راهحل برای این شرایط است که تعداد پارامترهای آزاد را به عمیقتر کردن شبکه کاهش میدهد.[7]
لایههای ادغام
لایههای ادغام (pooling layer): شبکههای عصبی پیچشی ممکن است شامل لایههای ادغام محلی یا سراسری باشند که خروجیهای خوشههای نورونی در یک لایه را در یک تکنورون در لایه بعدی ترکیب میکند.[8] به عنوان مثال روش حداکثر تجمع (max pooling) حداکثر مقدار بین خوشههای نورونی در لایه پیشین استفاده میکند.[9] مثال دیگر میانگین تجمع (average pooling) است که از مقدار میانگین خوشههای نورونی در لایه پیشین استفاده میکند.
کاملاً همبند
لایههای کاملاً همبند، هر نورون در یک لایه را به هر نورون در لایه دیگر متصل میکنند. این رویکرد در اصل مشابه کاری است که در شبکه عصبی پرسپترون چند لایه (MLP) انجام میشود.
وزنها
شبکههای عصبی پیچشی وزنها را در لایههای پیچشی به اشتراک میگذارند که باعث میشود حداقل حافظه و بیشترین کارایی بدست بیاید.
شبکههای عصبی متأخر
برخی شبکههای عصبی متأخر از معماری مشابهی استفاده میکنند، مخصوصاً آنهایی که برای تشخیص تصویر یا طبقهبندی استفاده میشوند.[10]
یادگیری
یادگیری ماشینی با نظارت (supervised learning) به دنبال تابعی از میان یک سری توابع هست که تابع هزینه (loss function) داده ها را بهینه سازد. به عنوان مثال در مسئله رگرسیون تابع هزینه میتواند اختلاف بین پیشبینی و مقدار واقعی خروجی به توان دو باشد، یا در مسئله طبقه بندی ضرر منفی لگاریتم احتمال خروجی باشد. مشکلی که در یادگیری شبکه های عصبی وجود دارد این است که این مسئله بهینه سازی دیگر محدب (convex) نیست [11]. ازین رو با مشکل کمینههای محلی روبرو هستیم. یکی از روشهای متداول حل مسئله بهینه سازی در شبکههای عصبی بازگشت به عقب یا همان back propagation است[11]. روش بازگشت به عقب گرادیانِ تابع هزینه را برای تمام وزنهای شبکه عصبی محاسبه میکند و بعد از روشهای گرادیان کاهشی (gradient descent) برای پیدا کردن مجموعه وزنهای بهینه استفاده میکند.[12] روشهای گرادیان کاهشی سعی میکنند به صورت متناوب در خلاف جهت گرادیان حرکت کنند و با این کار تابع هزینه را به حداقل برسانند.[12] پیدا کردن گرادیانِ لایه آخر ساده است و با استفاده از مشتق جزئی بدست می آید. گرادیانِ لایههای میانی اما به صورت مستقیم بدست نمیآید و باید از روشهایی مانند قاعده زنجیری در مشتقگیری استفاده کرد.[12] روش بازگشت به عقب از قاعده زنجیری برای محاسبه گرادیانها استفاده میکند و همانطور که در پایین خواهیم دید، این روش به صورت متناوب گرادیانها را از بالاترین لایه شروع کرده آنها را در لایههای پایینتر «پخش» میکند.
بازگشت به عقب (Backpropagation)، روشی برا محاسبه گرادیانها
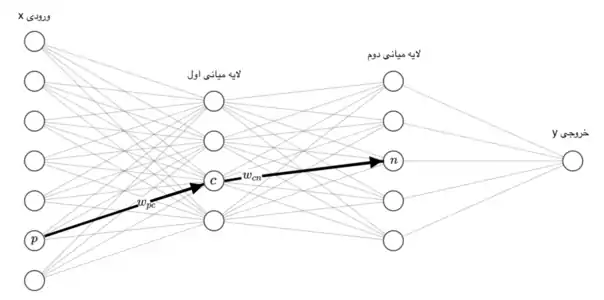
برای سلول عصبی ورودیی که از سلول عصبی به این سلول وارد میشود را با نشان میدهیم. وزن این ورودی است و مجموع ضرب ورودیها با وزنهایشان را با نمایش میدهیم، به این معنی که . حال باید بر روی تابعی غیر خطی اعمال کنیم این تابع را می نامیم و خروجی آن را با نمایش میدهیم یعنی . به همین شکل خروجیی که از سلول عصبی خارج شده و به سلول وارد میشود را با نمایش میدهیم و وزن آن را مینامیم. حال تمام وزنهای این شبکه عصبی را در مجموعهای به اسم میگنجانیم، هدف یادگیری این وزنهاست.[13] اگر ورودی ما باشد و خروجی و خروجی شبکه عصبی ما ، هدف پیدا کردن انتخاب است به قسمی که برای تمام دادهها و به هم خیلی نزدیک شوند. به عبارت دیگر هدف کوچک کردن یک تابع هزینه بر روی تمام داده هاست، اگر دادهها را با و تابع هزینه را با نشان دهیم هدف کمینه کردن تابع پایین است [14]:
به عنوان مثال اگر مسئله رگرسیون است برای میتوانیم خطای مربعات را در نظر بگیریم و اگر مسئله دستهبندی است برای میشود منفی لگاریتم بازنمایی را استفاده کرد.
برای بدست آوردن کمینه باید از روش گرادیان کاهشی استفاده کرد، به این معنی که گرادیان تابع را حساب کرده، کمی در خلاف جهت آن حرکت کرده و این کار را آنقدر ادامه داد تا تابع هزینه خیلی کوچک شود. روش بازگشت به عقب در واقع روشی برای پیدا کردن گرادیان تابع است.
حال فرض کنیم می خواهیم گرادیان تابع را نسبت به وزن بدست بیاوریم. برای این کار نیاز به قاعده زنجیری در مشتقگیری داریم. قاعده زنجیری به این شکل کار میکند: اگر تابعی داشته باشیم به اسم که وابسته به سه ورودی ، و باشد و هرکدام از این سه ورودی به نوبه خود وابسته به باشند، مشتق به به این شکل محاسبه میشود:
با استفاده از این قاعده زنجیری روش بازگشت به عقب را به این شکل دنبال میکنیم:
همانطور که در خط پیشین دیدیم برای بدست آوردن گرادیان نسبت به به دو مقدار نیاز داریم ورودی به سلول عصبی از سلول عصبی که همان است و راحت بدست می آید و که از روش بازگشتی بدست می آید و بستگی به هایی لایه بعد دارد که سلول به آنها وصل است، بهطور دقیقتر .
روش بازگشتی برای بدست آوردن ها به این شکل کار میکند که ابتدا را برای سلولهای لایه خروجی حساب میکنیم، و بعد لایهها را به نوبت پایین آئیم و برای هر سلول آن را با ترکیت های لایههای بالایی آن طبق فرمول حساب میکنیم. محاسبه کردن برای لایه خروجی آسان است و مستقیما با مشتق گرفتن از بدست میآید.[15]
تاریخچه
شبکههای عصبی پیچشی مشابه سیستم پردازش دیداری در موجودات زنده عمل میکنند. از قرن نوزدهم بهطور همزمان اما جداگانه از سویی نوروفیزیولوژیستها سعی کردند سیستم یادگیری و تجزیه و تحلیل مغز را کشف کنند، و از سوی دیگر ریاضیدانان تلاش کردند مدل ریاضی ای بسازند که قابلیت فراگیری و تجزیه و تحلیل عمومی مسائل را دارا باشد. اولین کوششها در شبیهسازی با استفاده از یک مدل منطقی در اوایل دههٔ ۱۹۴۰ توسط وارن مککالک و والتر پیتز انجام شد که امروزه بلوک اصلی سازنده اکثر شبکههای عصبی مصنوعی است. عملکرد این مدل مبتنی بر جمع ورودیها و ایجاد خروجی با استفاده از شبکهای از نورونها است. اگر حاصل جمع ورودیها از مقدار آستانه بیشتر باشد، اصطلاحاً نورون برانگیخته میشود. نتیجه این مدل اجرای ترکیبی از توابع منطقی بود.[16]
در سال ۱۹۴۹ دونالد هب قانون یادگیری را برای شبکههای عصبی طراحی کرد.[17] در سال ۱۹۵۸ شبکه پرسپترون توسط روزنبلات معرفی گردید. این شبکه نظیر واحدهای مدل شده قبلی بود. پرسپترون دارای سه لایه است که شامل لایهٔ ورودی، لایهٔ خروجی و لایهٔ میانی میشود. این سیستم میتواند یاد بگیرد که با روشی تکرارشونده وزنها را به گونهای تنظیم کند که شبکه توان بازتولید جفتهای ورودی و خروجی را داشتهباشد.[18] روش دیگر، مدل خطی تطبیقی نورون است که در سال ۱۹۶۰ توسط برنارد ویدرو و مارسیان هاف در دانشگاه استنفورد) به وجود آمد که اولین شبکههای عصبی به کار گرفته شده در مسائل واقعی بودند. آدالاین یک دستگاه الکترونیکی بود که از اجزای سادهای تشکیل شده بود، روشی که برای آموزش استفاده میشد با پرسپترون فرق داشت.
در سال ۱۹۶۹ میسکی و پاپرت کتابی نوشتند که محدودیتهای سیستمهای تک لایه و چند لایه پرسپترون را تشریح کردند. نتیجه این کتاب پیش داوری و قطع سرمایهگذاری برای تحقیقات در زمینه شبیهسازی شبکههای عصبی بود. آنها با طرح اینکه طرح پرسپترون قادر به حل هیچ مسئله جالبی نمیباشد، تحقیقات در این زمینه را برای مدت چندین سال متوقف کردند.
با وجود اینکه اشتیاق عمومی و سرمایهگذاریهای موجود به حداقل خود رسیده بود، برخی محققان تحقیقات خود را برای ساخت ماشینهایی که توانایی حل مسائلی از قبیل تشخیص الگو را داشته باشند، ادامه دادند. از جمله گراسبگ که شبکهای تحت عنوان Avalanch را برای تشخیص صحبت پیوسته و کنترل دست ربات مطرح کرد. همچنین او با همکاری کارپنتر شبکههای نظریه تشدید انطباقی را بنا نهادند که با مدلهای طبیعی تفاوت داشت. اندرسون و کوهونن نیز از اشخاصی بودند که تکنیکهایی برای یادگیری ایجاد کردند. ورباس در سال ۱۹۷۴ شیوه آموزش پس انتشار خطا را ایجاد کرد که یک شبکه پرسپترون چندلایه البته با قوانین نیرومندتر آموزشی بود.
پیشرفتهایی که در سال ۱۹۷۰ تا ۱۹۸۰ بدست آمد برای جلب توجه به شبکههای عصبی بسیار مهم بود. برخی فاکتورها نیز در تشدید این مسئله دخالت داشتند، از جمله کتابها و کنفرانسهای وسیعی که برای مردم در رشتههای متنوع ارائه شد. امروز نیز تحولات زیادی در تکنولوژی ANN ایجاد شدهاست.
منابع بیشتر
جستارهای وابسته
منابع
- LeCun, Yann. "LeNet-5, convolutional neural networks". Retrieved 16 November 2013.
- Zhang, Wei (1988). "Shift-invariant pattern recognition neural network and its optical architecture". Proceedings of annual conference of the Japan Society of Applied Physics.
- Zhang, Wei (1990). "Parallel distributed processing model with local space-invariant interconnections and its optical architecture". Applied Optics. 29 (32).
- Matusugu, Masakazu; Katsuhiko Mori; Yusuke Mitari; Yuji Kaneda (2003). "Subject independent facial expression recognition with robust face detection using a convolutional neural network" (PDF). Neural Networks. 16 (5): 555–559. doi:10.1016/S0893-6080(03)00115-1. Retrieved 17 November 2013.
- Collobert, Ronan; Weston, Jason (2008-01-01). "A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning". Proceedings of the 25th International Conference on Machine Learning. ICML '08. New York, NY, USA: ACM: 160–167. doi:10.1145/1390156.1390177. ISBN 978-1-60558-205-4.
- "Convolutional Neural Networks (LeNet) – DeepLearning 0.1 documentation". DeepLearning 0.1. LISA Lab. Retrieved 31 August 2013.
- Habibi,, Aghdam, Hamed. Guide to convolutional neural networks: a practical application to traffic-sign detection and classification. Heravi, Elnaz Jahani,. Cham, Switzerland. ISBN 978-3-319-57549-0. OCLC 987790957.
- Krizhevsky, Alex. "ImageNet Classification with Deep Convolutional Neural Networks" (PDF). Archived from the original (PDF) on 12 May 2013. Retrieved 17 November 2013.
- Ciresan, Dan; Meier, Ueli; Schmidhuber, Jürgen (June 2012). "Multi-column deep neural networks for image classification". 2012 IEEE Conference on Computer Vision and Pattern Recognition. New York, NY: Institute of Electrical and Electronics Engineers (IEEE): 3642–3649. arXiv:1202.2745v1. doi:10.1109/CVPR.2012.6248110. ISBN 978-1-4673-1226-4. OCLC 812295155. Retrieved 2013-12-09.
- Le Callet, Patrick; Christian Viard-Gaudin; Dominique Barba (2006). "A Convolutional Neural Network Approach for Objective Video Quality Assessment" (PDF). IEEE Transactions on Neural Networks. 17 (5): 1316–1327. doi:10.1109/TNN.2006.879766. PMID 17001990. Retrieved 17 November 2013.
- Ian Goodfellow and Yoshua Bengio and Aaron Courville (۲۰۱۶). Deep learning. MIT Press. صص. ۲۰۰.
- Heaton, Jeff (2017-10-29). "Ian Goodfellow, Yoshua Bengio, and Aaron Courville: Deep learning". Genetic Programming and Evolvable Machines. 19 (1–2): 305–307. doi:10.1007/s10710-017-9314-z. ISSN 1389-2576.
- «Build with AI | DeepAI». DeepAI. بایگانیشده از اصلی در 17 اكتبر 2018. دریافتشده در 2018-10-24. تاریخ وارد شده در
|archivedate=را بررسی کنید (کمک) - A., Nielsen, Michael (2015). "Neural Networks and Deep Learning". Archived from the original on 22 اكتبر 2018. Retrieved 20 دسامبر 2018. Check date values in:
|archive-date=(help) - Russell, Stuart; results, search (2009-12-11). Artificial Intelligence: A Modern Approach (به English) (3 ed.). Boston Columbus Indianapolis New York San Francisco Upper Saddle River Amsterdam, Cape Town Dubai London Madrid Milan Munich Paris Montreal Toronto Delhi Mexico City Sao Paulo Sydney Hong Kong Seoul Singapore Taipei Tokyo: Pearson. p. 578. ISBN 9780136042594.
- فاست، مبانی شبکههای عصبی، ۳۰–۳۱.
- فاست، مبانی شبکههای عصبی، ۳۱.
- فاست، مبانی شبکههای عصبی، ۳۰–۳۱.