جسم افلاطونی

در هندسه فضایی، چندوجهی‌های منتظمِ محدب به جسم افلاطونی موسومند. می‌توان نشان داد که در فضای سه‌بعدی تنها پنج جسم افلاطونی هست، که عبارتند از:

1. چهاروجهی منتظم، متشکل از چهار مثلث متساوی‌الاضلاع،
2. شش‌وجهی منتظم (مکعب)، متشکل از شش مربع،
3. هشت‌وجهی منتظم، متشکل از هشت مثلث متساوی‌الاضلاع،
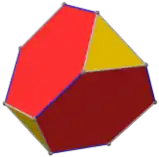
4. دوازده‌وجهی منتظم، متشکل از دوازده پنج‌ضلعی منتظم،
5. بیست‌وجهی منتظم، متشکل از بیست مثلث متساوی‌الاضلاع.

«چندوجهی‌های محدب منتظم» یا
اجسام افلاطونی
چهاروجهی منتظم
(پویانمایی) (مدل سه‌بعدی تعاملی)
شش‌وجهی منتظم (مکعب)
(پویانمایی) (مدل سه‌بعدی تعاملی)
هشت‌وجهی منتظم
(پویانمایی) (مدل سه‌بعدی تعاملی)
دوازده‌وجهی منتظم
(پویانمایی) (مدل سه‌بعدی تعاملی)
بیست‌وجهی منتظم
(پویانمایی) (مدل سه‌بعدی تعاملی)
• • •

وجه‌های هر کدام از این چندوجهی‌ها چندضلعی‌هایی منتظم و هم‌نهشتند و تعداد یکسانی از وجه‌ها در هر رأس آنان به یکدیگر می‌رسند. شش‌وجهی منتظم (مکعب) با هشت‌وجهی منتظم، دوازده‌وجهی منتظم با بیست‌وجهی منتظم، و چهاروجهی منتظم با خودش مزدوجند؛ یعنی با وصل کردن نقطهٔ وسط وجه‌های یکی می‌توان دیگری را ساخت. همچنین در ساخت دوازده‌وجهی منتظم و بیست‌وجهی منتظم نسبت طلایی پدید می‌آید.

عنوان این چندوجهی‌ها از نام افلاطون، فیلسوف یونانی، گرفته شده‌است که در نقل داستان آفرینش در دیالوگ تیمائوس، این چندوجهی‌ها را به عناصر تشکیل‌دهندهٔ گیتی نسبت می‌دهد. اقلیدس، فیثاغوری‌ها، و ابوالوفا بوزجانی نیز در باب اجسام افلاطونی پژوهش کرده‌اند. ستاره‌شناس آلمانی یوهانس کپلر هم هندسهٔ جهان را بر اساس اجسام افلاطونی می‌دانست و از ویژگی‌های آنان در وضع قوانین کپلر بهره برد. اجسام افلاطونی در آثار هنرمندانی چون موریس اشر و سالوادور دالی خودنمایی می‌کنند و در طبیعت نیز می‌توان آنان را در ساختارهای بلوری و هیبت برخی تک‌یاختگان و ویروس‌ها یافت.

تاریخ

تقارن و زیبایی اجسام افلاطونی الهام‌بخش معماران، هنرمندان، و صنعتگران از مصر باستان تا کنون بوده‌است،[1] و ویژگی‌های آنها پژوهشگران را از روزگار افلاطون تا رنسانس به‌خود مشغول داشته بود.[2] یافته‌های باستان‌شناختی از ۴٬۰۰۰ سال پیش در اسکاتلند هم شامل نقش‌هایی حک‌شده در سنگ از اجسام افلاطونی است.[3][4]

یونان باستان

ساختار هندسی عناصر هستی به گفتهٔ افلاطون

چهاروجهی	آتش
مکعب	خاک
هشت‌وجهی	هوا
دوازده‌وجهی	اثیر
بیست‌وجهی	آب

نخستین مطالعهٔ نظام‌مند دربارهٔ اجسام افلاطونی را فیثاغوری‌های یونان باستان انجام دادند.[5] ایشان بر این باور بودند که پنج جسم افلاطونی متناظر با ساختار عناصر چهارگانهٔ سازنده جهان هستند، یعنی چهاروجهی منتظم با نوک‌های تیز متناظر آتش، مکعبِ استوار متناظر خاک، و دو چندوجهی منتظم ساخته‌شده از مثلث دیگر (هشت‌وجهی منتظم و بیست‌وجهی منتظم) متناظر هوا و آب هستند. به باور ایشان دوازده‌وجهی منتظم نیز به شکلی مرموز نمایانگر کل هستی و ۱۲ صورت فلکی‌اش بود.[6][7] خود فیثاغورث (حدود ۵۸۰ تا ۵۰۰ پ.م.) احتمالاً چهاروجهی منتظم، مکعب، و دوازده‌وجهی منتظم را می‌شناخت.[8] او ۲۰ سال را در مصر گذرانده بود و احتمالاً این اطلاعات را آنجا آموخته بود.[9]

تحلیل ویژگی‌های اجسام افلاطونی و اثبات اینکه تنها پنج جسم افلاطونی وجود دارد نقطهٔ اوج کتاب پایانی اصول اقلیدس (حدود ۳۰۰ پ.م.) است.[10] به نوشتهٔ اقلیدس، اولین کسی که هشت‌وجهی و بیست‌وجهی منتظم را شرح داد تئائتتوس ریاضی‌دان آتنی و دوست افلاطون (حدود ۴۱۷–۳۶۹ پ.م.) بود.[11] از آنجا که افلاطون (۴۲۸/۴۲۷–۳۴۸/۳۴۷ پ.م.) نظریات فیثاغوری‌ها را در «داستان آفرینش» در دیالوگ تیمائوس تکرار کرده است، نام «جسم افلاطونی» به چندوجهی‌های منتظم اطلاق گردید.[12] افلاطون مانند فیثاغوری‌ها چهار تا از اجسام افلاطونی را به عناصر چهارگانه نسبت می‌داد. به نوشتهٔ او:

خداوند آب و هوا در وسط خاک و آتش قرار داد و بین همهٔ آنها تناسبی واحد برقرار ساخت […] به این ترتیب از پیوند این چهار عنصر، جسم جهان به وجود آمد و در سایهٔ تناسب، توازن و هماهنگی در درون آن حکمفرما گردید.

— تیمائوس[13]

افلاطون در این نوشته از دوازده‌وجهی منتظم به سرعت می‌گذرد و تنها جمله‌ای که دربارهٔ آن بیان می‌دارد این است که «خدا آن را در آفرینش کل جهان به کار برده‌است.»[14] مفسران افلاطون دوازده‌وجهی را با دوازده برج منطقةالبروج مرتبط دانسته‌اند.[15] افلاطون پس از بیان ساختار هر یک از عناصر چهارگانه، دربارهٔ تبدیل آنها به یکدیگر بحث می‌کند. به باور او خاک قابل تبدیل به عناصر دیگر نیست، چرا که از مربع ساخته شده، ولی آب و آتش و هوا را، که از مثلث ساخته شده‌اند، می‌توان با تناسبی خاص به یکدیگر تبدیل کرد.[16] افلاطون باور داشت این اجسام سایه یا بازتابی از جهان واقع هستند؛ بااین‌حال به گفتهٔ کَرِن فرنچ[persian-alpha 1] آرای افلاطون را باید علاوه بر رویکرد تحت‌اللفظی، با رویکردی متافیزیکی نیز بررسی کرد.[17]

قرون وسطی

تصویر یک بیست‌وجهی منتظم در کتاب در باب تناسب الهی اثر لئوناردو دا وینچی

ابوالوفا محمد بوزجانی (۳۲۸–۳۸۸ ه‍.ق.) هم در مطالعهٔ اجسام افلاطونی به کمک دوایر عظیمهٔ کره به طرح و ترسیم اجسام افلاطونی پرداخت و به دنبال آن به تجسم و ترسیم آثاری نو دست زد. در برابر پنج جسم افلاطونی که هریک از یک نوع چند ضلعی منتظم مانند مثلث، مربع یا پنج‌ضلعی تشکیل شده‌است، بوزجانی از پنج ترکیب کروی نام می‌برد که از ترکیب چندضلعی‌های منتظم تشکیل شده‌اند. پژوهش‌های بوزجانی غالباً متمرکز بر هندسهٔ ترسیمی بود، که مناسب کار صنعتگران و هنرمندان است. از جملهٔ مساعی او می‌توان به کتاب فیما یحتاج الیه الصانع من الاعمال الهندسه[persian-alpha 2] اشاره کرد که با استفاده از ویژگی‌های اجسام افلاطونی و ارشمیدسی، روشی برای ترسیم اشکال سادهٔ هندسی به‌صورت ترکیبی (یا موزاییک‌کاری) برای پوشاندن کره به دست می‌دهد که در گنبدها و سقف‌های پیچیده معماری اسلامی به کار می‌رود.[18][19] از نکات قابل توجه در کتاب بوزجانی این است که او ترسیم‌هایش را به شکل گسترده ارائه کرده‌است تا خواننده با تخیل خود بتواند آن‌ها را به شکل سه‌بعدی ببیند.[20] به گفتهٔ گلرو نجیب‌اوغلو، تفاوت رویکرد افلاطون و بوزجانی در این است که «اگر در اجسام افلاطونی وحدت ترکیب بر تکرار یکدست یک نوع چند ضلعی منتظم مانند مثلث متساوی‌الاضلاع، مربع و پنج‌ضلعی منتظم بر بدنهٔ کره قرار دارد، در اجسامی که بوزجانی بیان کرده وحدت شکلی بر توافق پی‌درپی دو نوع چندضلعی منتظم استوار است.»[21]

رنسانس و قرون جدید

هنرمندان دوران رنسانس به‌منظور بررسی ویژگی‌های پرسپکتیو در آثارشان به‌شکلی گسترده از اجسام افلاطونی بهره می‌بردند،[22] که نمونهٔ آن‌ها را می‌توان در موزائیک معروف پائولو آچلو (۱۳۹۷-۱۴۷۵ م.) در کلیسای جامع سینت مارکو در ونیز دید. همچنین لئوناردو دا وینچی (۱۴۵۲-۱۵۱۹ م.) در تصویرسازی‌هایش برای کتاب در باب تناسب الهی اثر لوکا پاچیولی اجسام افلاطونی را ترسیم و ویژگی‌های آنان (مانند نسبت طلایی) را بررسی کرده‌است.[23]

تصور یوهانس کپلر از منظومه شمسی، تشکیل‌شده از اجسام افلاطونی از رموز جهان (۱۵۹۶)

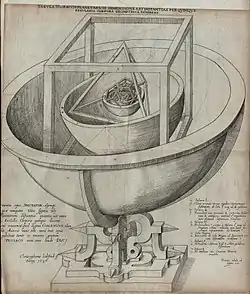
کیهان‌شناسی افلاطون در تیمائوس راهنمای مهم یوهانس کپلر (۱۵۷۱–۱۶۳۰ م.) در وضع قوانین کپلر بود.[24] کپلر در مدلش، ایدهٔ استفاده از جسم‌های افلاطونی برای تشریح هندسهٔ جهان را احیا کرد.[25][26] او اجسام افلاطونی را نه به‌عنوان شکل طبیعت و تعداد عناصر بلکه به عنوان مدلی از ساختار منظومهٔ شمسی می‌دانست.[27] کپلر در سال ۱۵۹۶ م. در کتاب رموز جهان هر کدام از شش سیارهٔ شناخته‌شده در آن زمان را به‌گونه‌ای نشان داد که روی سطح کره‌هایی هم‌ مرکز و جداشده با پنج جسم افلاطونی دور خورشید می‌گردند.[28] هدف کپلر در واقع این بود که فاصلهٔ میان سیاره‌ها را با استفاده از اجسام افلاطونی توصیف کند. او دریافت اگر کره‌ها و اجسام افلاطونی را به صورت یکی داخل دیگری قرار دهد، نسبت فواصل کره‌ها از مرکز مدلش در مقایسه به شکلی «بسیار خوب» بر نسبت فواصل سیارات از خورشید منطبق می‌شود. کپلر بر آن بود که توانسته قانون بنیادی طبیعت را کشف کند.[29] به نوشتهٔ آرتور کستلر:

[کپلر] در مدار کروی کیوان مکعبی را محاط کرد، و در آن مکعب کرهٔ دیگری را، که مدار مشتری بود. در آن چهاروجهی را محاط کرد و در آن چهاروجهی مدار کروی مریخ را. بین مدارهای مریخ و زمین، دوازده‌وجهی قرار گرفت و بین زمین و زهره، بیست‌وجهی، و بین زهره و عطارد، هشت‌وجهی. یوریکا!... این امر شیفتگی نهایی کپلر بود، چه به عنوان یک فرد و چه به عنوان نمونهٔ تاریخی. چرا که باور غلط او به پنج جسم کامل هوسی گذرا نبود. این باور با کمی تغییر و تعدیل تا آخر عمر با او ماند، که نشان از توهمی پارانویاگونه دارد. با این همه این وهم انگیزه و محرک او بود برای دستیابی به اکتشافات جاودانش.

— خوابگردها[30]

تیکو براهه (۱۵۴۶–۱۶۰۱ م.) نظریات کپلر را دربارهٔ شکل منظومهٔ شمسی رد کرد و کپلر را دعوت کرد که به رصدخانهٔ او در پراگ برود. کپلر، در تلاش برای حل ناهماهنگی بین مدلش از هستی و مشاهدات براهه، به این کشف مهم نایل شد که سیارات در مداری بیضوی و نه مدور به دور خورشید می‌گردند.[31]

در تاریخ معاصر

دوازده‌وجهی خالی‌ در تقدیس شام آخر اثر سالوادور دالی

موریس اِشرِ هلندی (۱۸۹۸-۱۹۷۲ م.) از اشکال خالص اجسام افلاطونی در آثارش به‌صورت گسترده استفاده کرده‌است. برای مثال اثر حکاکی روی چوب ستاره‌ها ترکیبی از مکعب‌ها و هشت‌وجهی‌ها را به تصویر می‌کشد که آفتاب‌پرست‌هایی را محیط کرده‌اند.[32] اشر در اثر دیگری با عنوان خزندگان از یک دوازده‌وجهی به‌عنوان نماد آسمان بهره می‌برد. شیفتگی اشر نسبت به اجسام افلاطونی تا حدی بود که تنها چیزی که پس از نقل مکان از کارگاهش با خود برد مجموعه‌ای درهم‌رفته از اجسام افلاطونی بود.[33] نقاش اسپانیایی سالوادور دالی (۱۹۰۴-۱۹۸۹ م.) نیز شیفتهٔ اجسام افلاطونی بود. در تصلیب دالی صلیبی را مشتمل بر هشت مکعب به تصویر می‌کشد و در تقدیس شام آخر دوازده‌وجهی خالی‌ای (که نماد «خدا» است) بر فراز سر مسیح و حواریونش قرار دارد. برونو موناری (۱۹۰۷-۱۹۹۸ م.) نیز مساعی گسترده‌ای در طراحی صنعتی با استفاده از شکل اجسام افلاطونی کرده‌است. زیرسیگاری مکعبی او نمونهٔ شاخص طراحی ایتالیایی در میانهٔ قرن بیستم است.[34] در قرن بیستم استفاده از اشکال خالص افلاطونی به یکی از ویژگی‌های سبک بین‌المللی معماری بدل شد. معمار سوئیسی لوکوربوزیه نیز سیستمی برای طراحی متناسب با ابعاد بدن انسان ارائه کرد که از نسبت طلایی بهره گرفته‌است.[35] اساس باکمینستر فولر در ساخت گنبد ژئودزیک نیز بیست‌وجهی منتظم بود.[36]

اهمیت و کاربرد

بلور سدیم کلراید	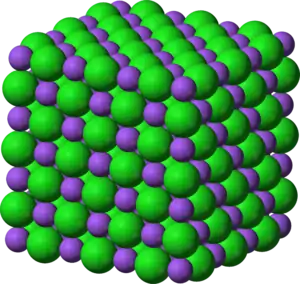ساختار سدیم کلراید
بلور کلسیم فلوراید	ساختار کلسیم فلوراید
بلور پیریت	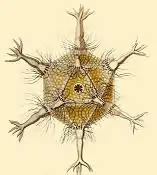گونه‌ای از شعاعیان با ساختار بیست‌وجهی
از جسم‌های افلاطونی به شکل گسترده به عنوان تاس استفاده می‌شود.	دودکاهدران، یکی از هیدروکربن‌های افلاطونی

با اینکه اجسام افلاطونی، بر خلاف آرای افلاطون، واحدهای ساختاری هستی نیستند، برخی مولکول‌ها و اتم‌های فشرده، به‌ویژه ساختارهای بلوری، شکلی شبیه اجسام افلاطونی دارند.[37] سنگ نمک (NaCl یا نمک خوراکی طبیعی) گاه در بلورهای مکعبی شکل می‌گیرد و بلورهای فلئوریت (CaF₂ یا کلسیم فلوراید) شبیه هشت‌وجهی‌اند. پیریت (FeS₂، معروف به طلای احمق‌ها) هم در ساختارهای مکعبی، هشت‌وجهی، و دوازده‌وجهی یافت می‌شود.[38] در سال ۲۰۱۱ نیز دانشمند اسرائیلی دن شختمن برای کشف ساختار بیست‌وجهی منتظم کریستال مایع آلومینیم جایزه نوبل شیمی را دریافت کرد.[39] هیدروکربن‌های افلاطونی هم نمایش مولکولی چند جسم افلاطونی‌اند که در آن‌ها رأس‌ها با اتم‌های کربن و اضلاع با پیوند کربن-کربن جایگزین شده‌است. از هیدروکربن‌های افلاطونی کوبان (C₈H₈) و دودِکاهدران (C₂₀H₂₀) سنتز شده‌اند و پیش‌بینی می‌شود تتراهدران (C₄H₄) از لحاظ جنبشی پایدار باشد.[40]

در اوایل قرن بیستم، ارنست هکل در کتاب اشکال هنری در طبیعت[persian-alpha 3] برخی شعاعیان را توصیف کرد که اسکلتی شبیه اجسام افلاطونی دارند.[41] ساختار برخی ویروس‌ها مثل تب‌خال نیز به شکل بیست‌وجهی منتظم است. به نوشتهٔ کریک و واتسون، بهینه‌ترین و ساده‌ترین حالت‌های ترکیب زیرساختارهای پروتئینی در ویروس برای تشکیل کپسید به شکل اجسام افلاطونی (و به‌ویژه بیست‌وجهی) است. ساده‌ترین کپسیدهای بیست‌وجهی با استفاده از ۳ زیرواحد همسان برای تشکیل هر وجه مثلثی ساخته می‌شوند. این بدین معنی است که برای ساختن یک کپسید کامل، به ۶۰ زیرواحد همسان نیاز است.[42]

از هر پنج جسم افلاطونی در بازی‌های شانس به عنوان تاس استفاده می‌شود،[43] و همچنین پازل‌های ترکیبی (مثل مکعب روبیک) به شکل همهٔ اجسام افلاطونی وجود دارد.

قضایا و ویژگی‌ها

اثبات هندسی

تعریف

جدول مشخصات اجسام افلاطونی

نام فارسی	چهاروجهی منتظم	شش‌وجهی منتظم (مکعب)	هشت‌وجهی منتظم	دوازده‌وجهی منتظم	بیست‌وجهی منتظم
نام انگلیسی	Tetrahedron	Hexahedron (Cube)	Octahedron	Dodecahedron	Icosahedron
تعداد وجه‌ها	چهار تا سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع)	شش تا چهارضلعی منتظم (مربع)	هشت تا سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع)	دوازده تا پنج‌ضلعی منتظم	بیست تا سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع)
شِما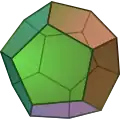
شکل گسترده
پویانمایی گسترش
وجه‌ها در هر راس	سه تا	سه تا	چهار تا	سه تا	پنج تا
دیاگرام راس
مجموع زوایای بین اضلاع در هر راس	۱۸۰°	۲۷۰°	۲۴۰°	۳۲۴°	۳۰۰°
تعداد راس	۴	۸	۶ (۲ × ۳)	۱۲ (۴ × ۳)	۲۰ (۸ + ۴ × ۳)
تعداد ضلع	۶	۱۲	۱۲	۳۰	۳۰
آرایش راس‌ها	۳٫۳٫۳	۴٫۴٫۴	۳٫۳٫۳٫۳	۵٫۵٫۵	۳٫۳٫۳٫۳٫۳
نماد شلفلی	{۳, ۳}	{۴, ۳}	{۳, ۴}	{۵, ۳}	{۳, ۵}

یک چندوجهی محدب جسم افلاطونی است، اگر و تنها اگر

1. همهٔ وجه‌های آن چندضلعی‌های منتظم هم‌نهشت باشند.
2. هیچ‌کدام از وجه‌های آن با هم تلاقی نکنند، مگر در اضلاع آن.
3. تعداد یکسانی از وجه‌ها در هر یک از رأس‌ها به هم برسند.

به مجموع وجه‌ها و ضلع‌هایی که در یک رأس به هم می‌رسند «هرم رأس»[persian-alpha 4] گفته می‌شود. منظور از هرم در اینجا یال هرم است و قاعدهٔ این هرم ممکن است مسطح نباشد.[44]

اگر مجموع زوایای بین ضلع‌های که در یک رأس به هم می‌رسند کمتر از ‎۳۶۰° باشد، آن رأس «محدب» دانسته می‌شود. برای اینکه یک چندوجهی محدب باشد، همهٔ رئوس آن باید محدب باشند.[45] حداقل تعداد وجه‌هایی که می‌توانند در یک ضلع به هم برسند تا تشکیل یک چندوجهی بدهند سه تا است.[46]

وجه‌های سه‌ضلعی

با به‌هم رسیدن سه سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع) در هر رأس، چهاروجهی منتظم تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۳ × ۶۰° = ۱۸۰° می‌شود که از ۳۶۰° کمتر است، بنابراین چهاروجهی منتظم جسم افلاطونی است.[47] با به‌هم رسیدن چهار سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع) در هر رأس، هشت‌وجهی منتظم تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۴ × ۶۰° = ۲۴۰° می‌شود که از ۳۶۰° کمتر است، بنابراین هشت‌وجهی منتظم نیز جسم افلاطونی است.[48] همچنین با به‌هم رسیدن پنج سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع) در هر رأس، بیست‌وجهی منتظم تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۵ × ۶۰° = ۳۰۰° می‌شود که از ۳۶۰° کمتر است، بنابراین بیست‌وجهی منتظم جسم افلاطونی است.[49] با به‌هم رسیدن شش سه‌ضلعی منتظم (مثلث متساوی‌الاضلاع) در هر رأس، مجموع زوایا در هر راس برابر ۶ × ۶۰° = ۳۶۰° می‌شود که از ۳۶۰° کمتر نیست و نمی‌توان تشکیل چندوجهی محدب داد. با افزایش تعداد سه‌ضلعی‌های منتظم به‌هم‌رسیده بعد از شش تا، مجموع زوایای اضلاع به‌هم‌رسیده در یک رأس همیشه از ۳۶۰° بیشتر خواهد بود و چندوجهی محدب تشکیل نمی‌شود؛ بنابراین تنها سه جسم افلاطونی با وجوه مثلثی می‌توان ساخت.[50]

وجه‌های چهارضلعی

با به‌هم رسیدن سه چهارضلعی منتظم (مربع) در هر رأس، شش‌وجهی منتظم (مکعب) تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۳ × ۹۰° = ۲۷۰° می‌شود که از ۳۶۰° کمتر است، بنابراین شش‌وجهی منتظم (مکعب) جسم افلاطونی است.[51] با به‌هم رسیدن چهار چهارضلعی منتظم (مربع) در هر رأس، مجموع زوایا در هر رأس برابر ۴ × ۹۰° = ۳۶۰° می‌شود که از ۳۶۰° کمتر نیست و نمی‌توان تشکیل چندوجهی محدب داد. با افزایش تعداد مربع‌های به‌هم‌رسیده، مجموع زوایای اضلاع به‌هم‌رسیده در یک رأس همیشه از ۳۶۰° بیشتر خواهد بود و چندوجهی محدب تشکیل نمی‌شود؛ بنابراین تنها یک جسم افلاطونی با وجوه مربعی می‌توان ساخت.[52]

وجه‌های پنج‌ضلعی

با به‌هم رسیدن سه پنج‌ضلعی منتظم در هر رأس، دوازده‌وجهی منتظم تشکیل می‌شود. مجموع زوایا در هر رأس برابر ۳ × ۱۰۸° = ۳۲۴° می‌شود که از ۳۶۰° کمتر است، بنابراین دوازده‌وجهی منتظم جسم افلاطونی است.[53] با به‌هم رسیدن چهار پنج‌ضلعی منتظم در هر رأس، مجموع زوایا در هر راس برابر ۴ × ۱۰۸° = ۴۳۲° می‌شود که از ۳۶۰° کمتر نیست و نمی‌تواند تشکیل چندوجهی محدب بدهد. با افزایش تعداد پنج‌ضلعی به‌هم‌رسیده، مجموع زوایای اضلاع به‌هم‌رسیده در یک رأس همیشه از ۳۶۰° بیشتر خواهد بود و چندوجهی محدب تشکیل نمی‌شود؛ بنابراین تنها یک جسم افلاطونی با وجوه پنج‌ضلعی می‌توان ساخت.[54]

وجه‌های شش‌ضلعی و بیشتر

با به‌هم رسیدن سه شش‌ضلعی منتظم در هر رأس، مجموع زوایا در هر راس برابر ۳ × ۱۲۰° = ۳۶۰° می‌شود که از ۳۶۰° کمتر نیست و نمی‌تواند تشکیل چندوجهی محدب بدهد. برای هفت‌ضلعی منتظم این عدد برابر ۳ × ۱۲۸° = ۳۸۵° و برای برای هشت‌ضلعی منتظم این عدد ۳ × ۱۳۵° = ۴۰۵° است و با افزایش تعداد اضلاع وجوه این عدد همواره زیاد می‌شود؛ بنابراین با چندضلعی‌های منتظم با بیشتر از پنج ضلع نمی‌توان جسم افلاطونی ساخت. به‌این‌ترتیب تنها پنج جسم افلاطونی وجود دارد که عبارتند از چهاروجهی منتظم، شش‌وجهی منتظم (مکعب)، هشت‌وجهی منتظم، دوازده‌وجهی منتظم، و بیست‌وجهی منتظم.[55]

اثبات توپولوژیک

می‌توان، تنها با استفاده از اطلاعات ترکیبی اجسام افلاطونی، اثباتی کاملاً توپولوژییکی ارائه کرد. نکتهٔ مهم در این اثبات مشخصه اویلر است مبنی بر اینکه V − E + F = 2، و این امر که pF = 2E = qV، که در آن p تعداد اضلاع هر وجه است و q تعداد اضلاعی که در هر رأس به هم می‌رسند. از ترکیب این معادله‌ها نتیجه می‌شود:[56]

${\displaystyle {\frac {2E}{q}}-E+{\frac {2E}{p}}=2.}$

و پس از ساده‌سازی جبری:[57]

${\displaystyle {1 \over q}+{1 \over p}={1 \over 2}+{1 \over E}.}$

از آنجا که E همواره مثبت است پس:

${\displaystyle {\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.}$

با بهره‌گیری از این امر که p و q باید دستکم ۳ باشند، می‌توان نشان داد که پنج حالت مختلف برای {p, q} وجود دارد:[58]

• {۳,۳}  ———  (چهاروجهی منتظم)؛
• {۳,۴}  ———  (مکعب)؛
• {۴,۳}  ———  (هشت‌وجهی منتظم)؛
• {۳,۵}  ———  (دوازده‌وجهی منتظم)؛
• {۵,۳}  ———  (بیست‌وجهی منتظم).

ویژگی‌های ترکیبی

اطلاعات ترکیبی اجسام افلاطونی

جسم افلاطونی	تعداد وجوه (F یا q)	تعداد اضلاع (E یا p)	تعداد رئوس (V)
چهاروجهی	۴	۶	۴
شش‌وجهی (مکعب)	۶	۱۲	۸
هشت‌وجهی	۸	۱۲	۶
دوازده وجهی	۱۲	۳۰	۲۰
بیست وجهی	۲۰	۳۰	۱۲

نشان داده شد که هر جسم افلاطونی با نماد شِلَفْلی {p, q} نشان داده می‌شود که p تعداد اضلاع (یا رأس‌های) هر وجه و q تعداد وجه‌ها (یا اضلاعی) است که در هر رأس به یکدیگر می‌رسند. همهٔ اطلاعات ترکیبی این چندوجهی‌ها، شامل تعداد رأس‌ها (V)، اضلاع (E)، و وجه‌ها (F) با استفاده از p و q قابل تعیین هستند. از آنجا که هر ضلع، دو رأس را به یکدیگر متصل کرده و دو وجه مجاور دارد، رابطهٔ زیر برقرار است:[59]

${\displaystyle pF=2E=qV.\,}$

مشخصهٔ اویلر

رابطهٔ دیگر بین اطلاعات ترکیبی اجسام افلاطونی با استفاده از مشخصه اویلر بدست می‌آید:[60]

${\displaystyle V-E+F=2.\,}$

یعنی برای هر جسم افلاطونی، تعداد رئوس منهای تعداد اضلاع به‌علاوهٔ تعداد وجه‌ها برابر ۲ است. مثلاً در مکعب داریم: ۸ – ۱۲ + ۶ = ۲. مشخصهٔ اویلر، که برای همهٔ چندوجهی‌های بدون حفره صادق است، برای اثبات قضیه‌های مختلفی در خصوص اجسام افلاطونی به کار می‌رود.[61]

به مثابه پیکربندی

پیکربندی در صفحه مجموعه‌ای است از N₀ تا نقطه و N₁ تا خط، که از هر کدام از نقطه‌ها N₀₁ تا خط بگذرد و روی هر خط N₁₀ تا نقطه قرار داشته بگیرد. می‌توان نشان داد که:[62]

${\displaystyle N_{0}N_{0}1=N_{1}N_{1}0}$

برای مثال، هر p-ضلعی یک پیکربندی است که در آن N₁ = N₀ = p (یعنی هر p-ضلعی p تا ضلع و رأس دارد) و N₀₁ = N₁₀ = 2 (یعنی از هر رأس p-ضلعی دو ضلع می‌گذرد و روی هر ضلع آن p رأس قرار دارد). با تعمیم پیکربندی در هندسهٔ فضایی، می‌توان آن را مجموعه‌ای از N₀ تا نقطه، N₁ تا خط، و N₂ تا صفحه دانست، و می‌توان به‌طور خلاصه گفت N_j تا j-فضا (که در آن ۰-فضا همان نقطه، ۱-فضا همان خط، و ۲-فضا همان صفحه است) با N_jk تا k-فضا برخورد می‌کنند (j ≠ k). می‌توان نشان داد که:[63]

${\displaystyle N_{j}N_{jk}=N_{k}N_{kj}}$

این اعداد را می‌توان به‌سادگی در یک ماتریس نمایش داد:[64]

${\displaystyle {\begin{bmatrix}N_{00}&N_{01}&N_{02}\\N_{10}&N_{11}&N_{12}\\N_{20}&N_{21}&N_{22}\end{bmatrix}}.}$

مفهوم پیکربندی اصولا در هندسه تصویری مورد مطالعه قرار می‌گیرد و در آن می‌توان با بهره‌گیری از اصل دوگانگی، رابطهٔ بین نقاط و صفحه‌های متناظر را حفظ کرد. به این مفهوم به‌ویژه در مورد اجسام افلاطونی توجه می‌شود، چرا که با چرخاندن ماتریس هر جسم افلاطونی به اندازهٔ ۱۸۰‌ درجه می‌توان ماتریس مزدوج آن را نوشت. برای هر جسم افلاطونی با نماد شلفلی {p, q} ماتریس پیکربندی به این شکل است:[65]

${\displaystyle {\begin{bmatrix}N_{0}&q&q\\2&N_{1}&2\\p&p&N_{2}\end{bmatrix}}.}$

ماتریس پیکربندی هر پنج جسم افلاطونی در جدول زیر آمده است.

{p,q}	پیکربندی افلاطونی
رتبهٔ گروه (g)	g=24	g=48		g=120
v e f v g/2q q q e 2 g/4 2 f p p g/2p	{3,3} (چهاروجهی) 4 3 3 2 6 2 3 3 4	{3,4} (مکعب) 6 4 4 2 12 2 3 3 8	{4,3} (هشت‌وجهی) 8 3 3 2 12 2 4 4 6	{3,5} (دوازده‌وجهی) 12 5 5 2 30 2 3 3 20	{5,3} (بیست‌وجهی) 20 3 3 2 30 2 5 5 12
g = 8pq/(4-(p-2)(q-2))

زاویه‌ها

زاویهٔ دوسطحی، زاویهٔ داخلی بین هر دو وجه چندوجهی است. اندازهٔ زاویهٔ دوسطحی، θ، برای چندوجهی {p,q} با استفاده فرمول زیر بدست می‌آید:

${\displaystyle \sin {\theta \over 2}={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}.}$

کاستی زاویه‌ای هر رأس یک چندوجهی، اختلاف بین مجموع زوایای بین وجه‌ها در هر رأس و 2π (بر حسب رادیان) است. کاستی زاویه‌ای، δ، در هر رأس جسم افلاطونی {p,q}، با استفاده از رابطهٔ زیر بدست می‌آید:

${\displaystyle \delta =2\pi -q\pi \left(1-{2 \over p}\right).}$

با استفاده از قضیه دکارت در باب مجموع کاستی‌ها،[persian-alpha 5] این مقدار برابر است با 4π تقسیم بر تعداد رأس‌ها (مجموع کاستی‌ها در همهٔ رأس‌ها 4π است).[67]

معادل سه‌بعدی زاویهٔ سطحی، زاویهٔ فضایی است. زاویهٔ فضایی، Ω، در رأس یک جسم افلاطونی، بر حسب زاویهٔ دوسطحی، به‌صورت زیر بدست می‌آید:

${\displaystyle \Omega =q\theta -(q-2)\pi .\,}$

زاویه‌های مربوط به اجسام افلاطونی در جدول زیر ارائه شده‌اند. مقدار زوایای فضایی بر حسب استرادیان داده شده‌است. ثابت ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$، نسبت طلایی است.

چندوجهی	زاویه دوسطحی (θ)	tan θ2	کاستی زاویه‌ای (δ)	زاویه فضایی رأس (Ω)	زاویه فضایی وجه
چهاروجهی	۷۰٫۵۳°	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle \pi }$	${\displaystyle \cos ^{-1}\left({\frac {23}{27}}\right)\quad \approx 0.551286}$	${\displaystyle \pi }$
مکعب	۹۰°	${\displaystyle 1}$	${\displaystyle \pi \over 2}$	${\displaystyle {\frac {\pi }{2}}\quad \approx 1.57080}$	${\displaystyle 2\pi \over 3}$
هشت‌وجهی	۱۰۹٫۴۷°	${\displaystyle {\sqrt {2}}}$	${\displaystyle {2\pi } \over 3}$	${\displaystyle 4\sin ^{-1}\left({1 \over 3}\right)\quad \approx 1.35935}$	${\displaystyle \pi \over 2}$
هشت‌وجهی	۱۱۶٫۵۷°	${\displaystyle \varphi }$	${\displaystyle \pi \over 5}$	${\displaystyle \pi -\tan ^{-1}\left({\frac {2}{11}}\right)\quad \approx 2.96174}$	${\displaystyle \pi \over 3}$
دوازده‌وجهی	۱۳۸٫۱۹°	${\displaystyle \varphi ^{2}}$	${\displaystyle \pi \over 3}$	${\displaystyle 2\pi -5\sin ^{-1}\left({2 \over 3}\right)\quad \approx 2.63455}$	${\displaystyle \pi \over 5}$

شعاع، مساحت، و حجم

همهٔ اجسام افلاطونی، سه کره هم‌مرکز دارند:

• کرهٔ محیطی که از همهٔ رأس‌ها عبور می‌کند،
• کرهٔ میانی که بر همهٔ اضلاع در نقطهٔ وسط ضلع مماس است،
• کره محاطی که بر همه وجه‌ها در مرکز وجه مماس است.

شعاع این کره‌ها، «شعاع محیطی»،[persian-alpha 6] «شعاع میانی»،[persian-alpha 7] و «شعاع محاطی»[persian-alpha 8] نامیده می‌شوند که به‌ترتیب برابر با فاصله مرکز چندوجهی از رأس‌ها، نقطه وسط اضلاع و مرکز وجه‌ها هستند. شعاع مح‍یطی (R) و شعاع محاطی (r) برای چندوجهی {p, q} با طول ضلع a از رابطهٔ زیر بدست می‌آید:[68]

${\displaystyle R=\left({a \over 2}\right)\tan {\frac {\pi }{q}}\tan {\frac {\theta }{2}}}$
${\displaystyle r=\left({a \over 2}\right)\cot {\frac {\pi }{p}}\tan {\frac {\theta }{2}}}$

که θ، زاویهٔ دوسطحی است.

مساحت سطح کل جسم (A) برای یک جسم افلاطونی {p, q} به آسانی و با استفاده از ضرب تعداد وجه‌ها (F) در مساحت p-ضلعی منتظم بدست می‌آید:[69]

${\displaystyle A=\left({a \over 2}\right)^{2}Fp\cot {\frac {\pi }{p}}.}$

شعاع میانی ρ با استفاده از رابطهٔ زیر بدست می‌آید:[70]

${\displaystyle \rho =\left({a \over 2}\right){\frac {\cos \left({\frac {\pi }{p}}\right)}{\sin \left({\frac {\pi }{h}}\right)}}}$

حجم اجسام افلاطونی برابر است با حاصل‌ضرب F در حجم هرمی با قاعده p-ضلعی منتظم و ارتفاع شعاع داخلی r:[71]

${\displaystyle V={\tfrac {1}{3}}rA.}$

جدول زیر، شعاع‌ها، مساحت و حجم اجسام افلاطونی را ارائه کرده‌است. در این جدول، طول ضلع a = 2 در نظر گرفته شده‌است.[72]

چندوجهی	شعاع محاطی (r)	شعاع میانی (ρ)	شعاع محیطی (R)	مساحت سطح (A)	حجم (V)	ضریب حجم (طول ضلع = ۱)
چهاروجهی	${\displaystyle 1 \over {\sqrt {6}}}$	${\displaystyle 1 \over {\sqrt {2}}}$	${\displaystyle {\sqrt {3 \over 2}}}$	${\displaystyle 4{\sqrt {3}}}$	${\displaystyle {\frac {\sqrt {8}}{3}}\approx 0.942809}$	${\displaystyle \approx 0.117851}$
مکعب	${\displaystyle 1\,}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle {\sqrt {3}}}$	${\displaystyle 24\,}$	${\displaystyle 8\,}$	${\displaystyle 1\,}$
هشت‌وجهی	${\displaystyle {\sqrt {2 \over 3}}}$	${\displaystyle 1\,}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle 8{\sqrt {3}}}$	${\displaystyle {\frac {\sqrt {128}}{3}}\approx 3.771236}$	${\displaystyle \approx 0.471404}$
دوازده‌وجهی	${\displaystyle {\frac {\varphi ^{2}}{\xi }}}$	${\displaystyle \varphi ^{2}}$	${\displaystyle {\sqrt {3}}\,\varphi }$	${\displaystyle 12{\sqrt {25+10{\sqrt {5}}}}}$	${\displaystyle {\frac {20\varphi ^{3}}{\xi ^{2}}}\approx 61.304952}$	${\displaystyle \approx 7.663119}$
بیست‌وجهی	${\displaystyle {\frac {\varphi ^{2}}{\sqrt {3}}}}$	${\displaystyle \varphi }$	${\displaystyle \xi \varphi }$	${\displaystyle 20{\sqrt {3}}}$	${\displaystyle {\frac {20\varphi ^{2}}{3}}\approx 17.453560}$	${\displaystyle \approx 2.181695}$

ثابت‌های φ و ξ در جدول بالا عبارتند از:

${\displaystyle \varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}}\qquad \xi =2\sin {\pi \over 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}=5^{\frac {1}{4}}\varphi ^{-{\frac {1}{2}}}}$

مختصات دکارتی و نسبت طلایی

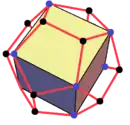
مختصات دکارتی چهاروجهی منتظم، مکعب، و هشت‌وجهی منتظم شامل نسبت طلایی (${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.6180}$) نیست و می‌توان آن‌ها را با اعداد طبیعی نشان دارد.[73] از سوی دیگر برای نمایش مختصات دکارتی دوازده‌وجهی منتظم و بیست‌وجهی منتظم به نسبت طلایی نیاز است. مختصات رئوس دوازده‌وجهی را می‌توان به‌سادگی از طریق رئوس سه مستطیل طلایی (مستطیلی که نسبت طول به عرض آن برابر 1:φ است) عمود برهم محاسبه کرد. اضلاع دوازده‌وجهی پاره‌خط‌هایی هستند که هر رأس مستطیل‌های طلایی را به پنج رأس همسایهٔ آن وصل می‌کنند.[74]

بیست‌وجهی منتظم را هم می‌توان با وصل کردن رئوس سه مستطیل عمود بر هم با نسبت طول به عرض 1:φ² به رئوس یک مکعب ایجاد کرد.[75]

مختصات دکارتی اجسام افلاطونی

شکل	سه‌وجهی منتظم		هشت‌وجهی منتظم	مکعب	بیست وجهی منتظم		دوازده‌وجهی منتظم
وجه‌ها	۴		۸	۶	۲۰		۱۲
رأس‌ها	۴		۶ (۲ × ۳)	۸	۱۲ (۴ × ۳)		۲۰ (۸ + ۴ × ۳)
جهت‌گیری مجموعه	۱	۲			۱	۲	۱	۲
مختصات رأس	(۱, ۱, ۱) (۱, −۱, −۱) (−۱, ۱, −۱) (−۱, −۱, ۱)	(−۱, −۱, −۱) (−۱, ۱, ۱) (۱, −۱, ۱) (۱, ۱, −۱)	(±۱, ۰, ۰) (۰, ±۱, ۰) (۰, ۰, ±۱)	(±۱, ±۱, ±۱)	(۰, ±۱, ±φ) (±۱, ±φ, ۰) (±φ, ۰, ±۱)	(۰, ±φ, ±۱) (±φ, ±۱, ۰) (±۱, ۰, ±φ)	(±۱, ±۱, ±۱) (0, ±۱φ, ±φ) (±۱φ, ±φ, ۰) (±φ, ۰, ±۱φ)	(±۱, ±۱, ±۱) (۰, ±φ, ±۱φ) (±φ, ±۱φ, ۰) (±۱φ, ۰, ±φ)
تصویر
حرف یونانی φ به نسبت طلایی ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.6180}$ اشاره دارد.

چندوجهی‌های مزدوج

با وصل کردن نقطهٔ وسط وجه‌های یک چندوجهی (یا به عبارت دیگر جابجا کردن تعداد وجه‌ها و رأس‌ها) مزدوج آن چندوجهی حاصل می‌شود. مزدوج هر جسم افلاطونی هم یک جسم افلاطونی است:[76]

بدون قاب

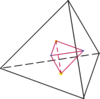
با متصل کردن نقطهٔ وسط وجوه یک چهاروجهی منتظم، یک چهاروجهی منتظم کوچکتر حاصل می‌شود (تعداد وجوه و رئوس چهاروجهی (۴) با هم برابر است).[77]

بدون قاب

بدون قاب

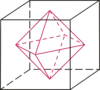
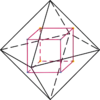
با متصل کردن نقطهٔ وسط وجوه یک شش‌وجهی منتظم (مکعب)، یک هشت‌وجهی منتظم حاصل می‌شود. همچنین با اتصال نقطهٔ وسط وجوه یک هشت‌وجهی منتظم، یک شش‌وجهی منتظم (مکعب) به‌دست می‌آید (تعداد وجوه مکعب با رئوس هشت‌وجهی (۶) برابر و رئوس آن (۸) با وجوه هشت‌وجهی برابر است).[78]

بدون قاب

بدون قاب

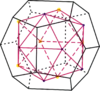
با متصل کردن نقطهٔ وسط وجوه یک دوازده‌وجهی منتظم، یک بیست‌وجهی منتظم حاصل می‌شود. همچنین با اتصال نقطهٔ وسط وجوه یک بیست‌وجهی منتظم، یک دوازده‌وجهی منتظم به‌دست می‌آید (تعداد وجوه دوازده‌وجهی با رئوس بیست‌وجهی (۱۲) برابر و رئوس آن (۲۰) با وجوه بیست‌وجهی برابر است).[79]

اگر نماد شلفلی یک چندوجهی {p, q} باشد، نماد شلفلی مزدوج آن {q, p} خواهد بود. به‌طور کلی هر ویژگی‌ ترکیبی یک جسم افلاطونی را می‌توان برابر ویژگی ترکیبی دیگری از مزدوج آن دانست.[80]

از آنجا که گروه تقارن هر چندوجهی با گروه تقارن مزدوج آن یکی است، تنها سه گروه تقارن در رابطه با اجسام افلاطونی مطرح می‌شود که عبارتند از:[81]

• تقارن چهاروجهی (گروه تقارن T)
• تقارن هشت‌وجهی (گروه تقارن O، که با گروه تقارن مکعب یکی است.)
• تقارن بیست‌وجهی (گروه تقارن I، که با گروه تقارن دوازده‌وجهی یکی است.)

گروه‌های تقارن اجسام افلاطونی در جدول زیر آمده است.

چندوجهی	نماد شلفلی	نماد ویتهاف[persian-alpha 9]	چندوجهی مزدوج	گروه تقارن
				گروه چندوجهی[persian-alpha 10]	نشانه‌گذاری شونفلیز[persian-alpha 11]	نشانه‌گذاری کاکستر[persian-alpha 12]	نشانه‌گذاری فراخمینه[persian-alpha 13]	رتبه گروه
چهاروجهی	{3, 3}	2 3	چهاروجهی	تقارن چهاروجهی	Td T	[3,3] [3,3]^+	*332 332	24 12
مکعب	{4, 3}	2 4	هشت‌وجهی	تقارن هشت‌وجهی	Oh O	[4,3] [4,3]^+	*432 432	48 24
هشت‌وجهی	{3, 4}	2 3	مکعب
دوازده‌وجهی	{5, 3}	2 5	بیست‌وجهی	تقارن بیست‌وجهی	Ih I	[5,3] [5,3]^+	*532 532	120 60
بیست‌وجهی	{3, 5}	2 3	دوازده‌وجهی

چندبرهای مرتبط

چندوجهی‌های نیمه‌منتظم

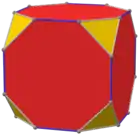
اجسام ارشمیدسی چندوجهی‌هایی هستند که از بیش از یک نوع چندضلعی همنهشت ساخته شده‌اند. در کل ۱۳ جسم ارشمیدسی وجود دارد[persian-alpha 14] که از این تعداد هفت تای آن‌ها را می‌توان با بریدن گوشه‌های اجسام افلاطونی ساخت. این هفت جسم ارشمیدسی عبارتند از:[82]

1. مکعب‌هشت‌وجهی، که هشت وجهش مثلث متساوی‌الاضلاع و شش وجهش مربعند و می‌توان آن را با بریدن گوشه‌های مکعب یا هشت‌وجهی منتظم از وسط اضلاع آن‌ها ساخت؛
2. بیست‌دوازده‌وجهی، که بیست وجهش مثلث متساوی‌الاضلاع و دوازده وجهش پنج‌ضلعی منتظمند و می‌توان آن را با بریدن گوشه‌های دوازده‌وجهی منتظم یا بیست‌وجهی منتظم از وسط اضلاع ساخت.[persian-alpha 15]
3. چهاروجهی بریده‌شده، که چهار وجهش شش‌ضلعی منتظم و چهار وجهش مثلث متساوی‌الاضلاعند و می‌توان آن را با بریدن گوشه‌های چهاروجهی منتظم تا ۱۳ درصد طول اضلاع ساخت.
4. مکعب بریده‌شده، که شش وجهش هشت‌ضلعی منتظم و هشت وجهش مثلث متساوی‌الاضلاعند و می‌توان آن را با بریدن گوشه‌های مکعب تا ۱۴ درصد طول اضلاع ساخت.
5. هشت‌وجهی بریده‌شده، که هشت وجهش شش‌ضلعی منتظم و شش وجهش مربعند و می‌توان آن را با بریدن گوشه‌های هشت‌وجهی منتظم تا ۱۳ درصد طول اضلاع ساخت.
6. دوازده‌وجهی بریده‌شده، که ۱۲ وجهش ده‌ضلعی منتظم و ۲۰ وجهش مثلث متساوی‌الاضلاعند و می‌توان آن را با بریدن گوشه‌های دوازده‌وجهی منتظم تا ۱۲+φ درصد طول اضلاع ساخت.
7. بیست‌وجهی بریده‌شده یا «توپ فوتبال»، که ۱۲ وجهش پنج‌ضلعی منتظم و ۲۰ وجهش شش‌ضلعی منتظمند و می‌توان آن را با بریدن گوشه‌های بیست‌وجهی منتظم تا ۱۳ درصد طول اضلاع ساخت.

• 
  مکعب‌هشت‌وجهی
• 
  بیست‌دوازده‌وجهی
• 
  چهاروجهی بریده‌شده
• 
  مکعب بریده‌شده
• 
  هشت‌وجهی بریده‌شده
• 
  دوازده‌وجهی بریده‌شده
• 
  بیست‌وجهی بریده‌شده

اجسام کاتالان را هم، که مزدوج اجسام ارشمیدسی‌اند، می‌توان ازین روش ساخت، بااین‌حال وجه‌های اجسام کاتالان همنهشت نیستند.

موزائیک‌کاری منتظم

سه نوع موزائیک‌کاری منتظم صفحه

{4,4}	{3,6}	{6,3}

موزائیک‌کاری صفحه‌ها با استفاده از چندضلعی منتظم محدب به‌طوری که اضلاع واحدها روی هم بیفتند و درزی باقی نماند (اصطلاحاً «لانه‌زنبوری دوبعدی»[persian-alpha 16]) به سه روش ممکن است که با سه گروه تقارن اجسام افلاطونی متناظرند؛ ازین رو می‌توان اجسام افلاطونی را موزائیک‌کاری منتظم سطح کُره‌ای هم‌مرکز با آن دانست. از سوی دیگر در مثلثات کروی می‌توان با تصویر اضلاع اجسام افلاطونی روی سطح کره واحدهای لازم برای پوشاندن سطح آن را بدست آورد.[83] روش ابوالوفا محمد بوزجانی برای پوشاندن سطح کره که برای پوشاندن گنبدها و سقف‌های پیچیده معماری اسلامی با اشکال سادهٔ هندسی به کار می‌رود[84] مبتنی بر همین ویژگی اجسام افلاطونی است.

موزائیک‌کاری افلاطونی کره

{3,3}	{4,3}	{3,4}	{5,3}	{3,5}

در بعدهای بالاتر

یک تصویرسازی سه‌بعدی از ۶۰۰-خانه، شیئی چهاربعدی که شرایط اجسام افلاطونی را احراز می‌کند. همانگونه که می‌توان از اشیاء سه‌بعدی عکس‌هایی دوبعدی تهیه کرد، از اشیاء چهاربعدی هم می‌توان تصاویری سه‌بعدی انداخت.

در سال ۱۸۵۲، لودویگ شلفلیِ ریاضی‌دان ثابت کرد که در فضای چهاربعدی شش «چندوجهی» هست که شروط اجسام افلاطونی را احراز می‌کند.[85] در فضای پنج‌بعدی و فضاها در ابعاد بالاتر همیشه تنها سه «چندوجهی» وجود دارد که شروط اجسام افلاطونی را احراز می‌کند.[86] این چندبرها، که تعمیمی از اجسام افلاطونی هستند، عبارتند از ابرمکعب (مکعب n-بعدی)، سیمپلکس (چهاروجهی n-بعدی)، و ارتوپلکس (هشت‌وجهی n-بعدی).[87] علاوه بر سه چندبر، در فضای سه‌بعدی دو چندوجهی (دوازده‌وجهی منتظم و بیست‌وجهی منتظم) و در فضای چهاربعدی سه چندبر (معروف به ۲۴-خانه، ۱۲۰-خانه، و ۶۰۰-خانه) هست.[88]

جستارهای وابسته

• جسم ارشمیدسی
• جسم کاتالان

یادداشت

1. Karen L. French
2. در باب آنچه صنعتگران از مسائل هندسی نیاز دارند.
3. Art Forms in Nature
4. vertex pyramid
5. قضیهٔ دکارت در باب «مجموع کاستی‌ها» بیان می‌دارد که اگر یک چندوجهی با کره همسان‌ریخت باشد (یعنی اگر از دیدگاه توپولوژیکی بتوان آن را با یک کره یکسان در نظر گرفت)، مجموع کاستی‌های همهٔ رأس‌ها برابر دو دایرهٔ کامل (‎720° یا 4π) است.[66]
6. circumradius
7. midradius
8. inradius
9. Wythoff symbol
10. Polyhedral group
11. Schönflies notation
12. Coxeter notation
13. Orbifold notation
14. بدون به حساب آوردن منشورها و پادمنشور‌ها
15. با بریدن گوشه‌های چهاروجهی منتظم از وسط اضلاعش یک چهاروجهی منتظم کوچکتر حاصل می‌شود.
16. two-dimensional honeycomb

منابع

پانویس

1. Encyclopedia Britannica
2. Gardner 1987‏:‎14
3. French 2014‏:‎96
4. Sarhangi 2008‏:‎511–523
5. Gardner 1987‏:‎13
6. Gardner 1987‏:‎14
7. Encyclopedia Britannica
8. Encyclopedia Britannica
9. French 2014‏:‎96
10. Gardner 1987‏:‎14
11. افراسیابی ۱۳۸۹‏:‎۳–۱۰
12. Gardner 1987‏:‎14
13. هاشمی ۱۳۹۱‏:‎۲۶–۳۱
14. افراسیابی ۱۳۸۹‏:‎۳–۱۰
15. Kotrč 1981
16. افراسیابی ۱۳۸۹‏:‎۳–۱۰
17. French 2014‏:‎100
18. هاشمی ۱۳۹۱‏:‎۲۶–۳۱
19. Sarhangi 2008‏:‎511–523
20. Sarhangi 2008‏:‎511–523
21. هاشمی ۱۳۹۱‏:‎۲۶–۳۱
22. Sala 2004
23. Sala 2004
24. Encyclopedia Britannica - Geometry
25. Gardner 1987‏:‎14
26. Encyclopedia Britannica
27. Encyclopedia Britannica - Geometry
28. Encyclopedia Britannica - Geometry
29. مازوچی ۱۳۸۸‏:‎۱۲–۲۹
30. Senechal 2013‏:‎44
31. Encyclopedia Britannica - Geometry
32. Sala 2004
33. Form, Shape, and Space: Teachers' Booklet 2008‏:‎17
34. Sala 2004
35. Sala 2004
36. MacLean 2007‏:‎61
37. French 2014‏:‎96
38. French 2014‏:‎96
39. NIST 2017
40. Lewars 2008‏:‎185-226
41. Haeckel 2012, PLATE 1
42. Nayudu 2008‏:‎50
43. Gardner 1987‏:‎17
44. Pottmann et al. 2007‏:‎81
45. Pottmann et al. 2007‏:‎81
46. Pottmann et al. 2007‏:‎81
47. Pottmann et al. 2007‏:‎81
48. Pottmann et al. 2007‏:‎81
49. Pottmann et al. 2007‏:‎82
50. Pottmann et al. 2007‏:‎82
51. Pottmann et al. 2007‏:‎81
52. Pottmann et al. 2007‏:‎81
53. Pottmann et al. 2007‏:‎83
54. Pottmann et al. 2007‏:‎83
55. Pottmann et al. 2007‏:‎83
56. Henle 1994‏:‎9
57. Henle 1994‏:‎9
58. Henle 1994‏:‎9
59. Cromwell 1999‏:‎196
60. Pottmann et al. 2007‏:‎85
61. Pottmann et al. 2007‏:‎85
62. Coxeter 1973‏:‎12—13
63. Coxeter 1973‏:‎12—13
64. Coxeter 1973‏:‎12—13
65. Coxeter 1973‏:‎12—13
66. Cromwell 1999‏:‎187
67. Cromwell 1999‏:‎187
68. Whistler Alley Mathematics - Formula Derivations for Polyhedra 2016
69. Whistler Alley Mathematics - Formula Derivations for Polyhedra 2016
70. Whistler Alley Mathematics - Formula Derivations for Polyhedra 2016
71. Whistler Alley Mathematics 2011
72. Whistler Alley Mathematics 2011
73. Sacred Geometry 2012
74. Sacred Geometry 2012
75. Sacred Geometry 2012
76. Pottmann et al. 2007‏:‎86
77. Pottmann et al. 2007‏:‎86
78. Pottmann et al. 2007‏:‎86
79. Pottmann et al. 2007‏:‎86
80. Pottmann et al. 2007‏:‎86
81. Coxeter 1973‏:‎130
82. Pottmann et al. 2007‏:‎90
83. Coxeter 1973‏:‎58—59
84. هاشمی ۱۳۹۱‏:‎۲۶–۳۱
85. Pottmann et al. 2007‏:‎83
86. Pottmann et al. 2007‏:‎83
87. Pottmann et al. 2007‏:‎83
88. Pottmann et al. 2007‏:‎83

فهرست منابع

• Coxeter, H.S.M. (1973). Regular Polytopes. Dover books on advanced mathematics. Dover Publications. ISBN 978-0-486-61480-9. Archived from the original on 16 December 2018. Retrieved 2018-11-25.
• Cromwell, P.R. (1999). Polyhedra. Cambridge University Press. ISBN 978-0-521-66405-9. Archived from the original on 16 December 2018. Retrieved 2018-10-22.
• French, K.L. (2014). The Hidden Geometry of Life: The Science and Spirituality of Nature. Gateway series. Watkins Media Limited. ISBN 978-1-78028-845-1. Archived from the original on 16 December 2018. Retrieved 2018-11-12.
• Gardner, Martin (1987). "Chapter 1: The Five Platonic Solids". The 2nd Scientific American book of mathematical puzzles & diversions. Chicago: University of Chicago Press. ISBN 0-226-28253-8. OCLC 15550017.
• Haeckel, E. (2012). Art Forms in Nature. Dover Pictorial Archive. Dover Publications. ISBN 978-0-486-15532-6. Archived from the original on 16 December 2018. Retrieved 2018-11-12.
• Henle, M. (1994). A Combinatorial Introduction to Topology. Dover Books on Mathematics Series. Dover. ISBN 978-0-486-67966-2. Archived from the original on 16 December 2018. Retrieved 2018-10-22.
• Kotrč, Ronald F. (1981). THE DODECAHEDRON IN PLATO'S "TIMAEUS". Rheinisches Museum für Philologie. J.D. Sauerländers Verlag. Archived from the original on 16 December 2018. Retrieved 2018-10-22.
• Lewars, Errol G. (2008). Modeling Marvels. Dordrecht: Springer Netherlands. doi:10.1007/978-1-4020-6973-4. ISBN 978-1-4020-6972-7.
• MacLean, K.J.M. (2007). A Geometric Analysis of the Platonic Solids and Other Semi-Regular Polyhedra. Geometric explorations series. Loving Healing Press. ISBN 978-1-932690-99-6. Archived from the original on 16 December 2018. Retrieved 2018-11-10.
• Nayudu, M.V. (2008). Plant Viruses. Tata McGraw-Hill. ISBN 978-0-07-065660-4. Archived from the original on 16 December 2018. Retrieved 2018-11-12.
• Pottmann, Helmut; Asperl, Andreas; Hofer, Michael; Kilian, Axel; Bentley, Daril (2007). Architectural geometry. Bentley Institute Press. ISBN 1-934493-04-X. OCLC 180177477.
• Sala, Nicoletta (2004). Art, Mathematics and Architecture for Humanistic Renaissance: the Platonic Solids (PDF). University of Italian Switzerland, Academy of Architecture, Switzerland.
• Sarhangi, Reza (2008). "Illustrating Abu al-Wafā' Būzjānī: Flat Images, Spherical Constructions". Iranian Studies. Informa UK Limited. 41 (4): 511–523. doi:10.1080/00210860802246184. ISSN 0021-0862.
• Senechal, M. (2013). Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination. EBSCOhost ebooks online. Springer New York. ISBN 978-0-387-92714-5. Archived from the original on 16 December 2018. Retrieved 2018-11-10.
• Tanna, S. (2014). Amazing Math: Introduction to Platonic Solids. CreateSpace Independent Publishing Platform. ISBN 978-1-5030-8485-8. Archived from the original on 16 December 2018. Retrieved 2018-09-15.
• "Form, Shape, and Space: Teachers' Booklet" (PDF). 2008. Archived from the original (PDF) on 16 December 2018. Retrieved 2018-10-22.
• "Geometry - mathematics". Encyclopedia Britannica. Archived from the original on 16 December 2018. Retrieved 2018-09-16.
• "Phi in Sacred Solids". Sacred Geometry. 2012-11-28. Archived from the original on 16 December 2018. Retrieved 2018-11-10.
• ""Platonic solid - MATHEMATICS"". Encyclopedia Britannica. Archived from the original on 16 December 2018. Retrieved 2018-09-06.
• "Formula Derivations for Polyhedra". Whistler Alley Mathematics. 2016-01-21. Archived from the original on 16 December 2018. Retrieved 2018-11-24.
• "Platonic Solids". Whistler Alley Mathematics. 2011-12-29. Archived from the original on 16 December 2018. Retrieved 2018-10-22.
• "The Nobel Moment: Dan Shechtman". NIST. 2017-05-02. Archived from the original on 16 December 2018. Retrieved 2018-11-12.

• افراسیابی، مرضیه (۱۳۸۹). «نقد و بررسی افلاطون: رساله تیمائوس: تبیین ریاضیاتی افلاطون از عالم طبیعت». کتاب ماه فلسفه (۳۸): ۳–۱۰. بایگانی‌شده از اصلی در ۱۶ دسامبر ۲۰۱۸. دریافت‌شده در ۲۰۱۸-۰۹-۱۶.
• مازوچی، ‌هادی (۱۳۸۸). «این هم مجموعه ای است . .». کتاب ماه علوم و فنون (۱۲۰): ۱۲–۲۹. بایگانی‌شده از اصلی در ۱۶ دسامبر ۲۰۱۸. دریافت‌شده در ۲۰۱۸-۰۹-۱۶.
• هاشمی، ‌غلامرضا (۱۳۹۱). «نظری به جایگه هندسه و نقوش هندسی در آرا متفکران یونانی و مسلمان». کتاب ماه هنر (۱۶۵): ۲۶–۳۱. بایگانی‌شده از اصلی در ۱۶ دسامبر ۲۰۱۸. دریافت‌شده در ۲۰۱۸-۰۹-۱۶.