تناظر دو سویه

در ریاضیات یک تناظر دو سویه (یا تناظر یک به یک) به تابعی میان اعضای دو مجموعه گفته می‌شود به شرط این که هر عضو از هر مجموعه با دقیقاً یک عضو از مجموعه دیگر جفت شده باشد. در هیچ‌کدام از مجموعه‌ها هیچ عضو بدون جفتی وجود ندارد.

تابع
x ↦ f (x)
مثال‌هایی با دامنه و دامنه مشترک
X → B, B → X, B^n → B X → Z, Z → X X → R, R → X, R^n → X X → C, C → X, C^n → X
کلاس‌ها/ویژگی‌ها
ثابت · همانی · خطی · چندجمله‌ای · گویا · جبری · تحلیلی · هموار · پیوسته · قابل اندازه‌گیری · یک‌به‌یک · پوشا · دوسویی
سازه‌های تابعی
محدود سازی · ترکیب · لاندا · وارون
تعمیم تابع
جزئی · چندمقداری · ضمنی

یک تناظر یک‌به‌یک

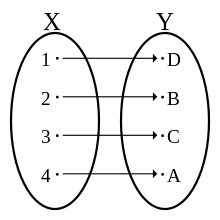
هر تابع دوسویی از مجموعهٔ X به مجموعهٔ Y دارای یک تابع وارون از Y به X است. اگر این دو مجموعه متناهی باشند در این صورت وجود تناظر یک‌به‌یک میان اعضای آن‌ها نشان‌دهندهٔ این است که تعداد اعضای این دو مجموعه برابر است. در مورد مجموعه‌های نامتناهی این تناظرها باعث به وجود آمدن مفهوم اعداد کاردینال شدند که روشی برای بررسی بی‌نهایت‌های متفاوت هستند.

هر تابع دوسویی از یک مجموعه به خود آن مجموعه جایگشت نام دارد.

توابع دوسویی برای بسیاری از مباحث ریاضی ابزاری ضروری هستند. به عنوان مثال: تعاریف یک‌ریختی و همسان‌ریختی.

تعریف

برای این که تابع f از مجموعه X و به مجموعهٔ Y دوسویی باشد باید چهار شرط زیر برقرار باشند:

1. هر عضو مجموعهٔ X باید با حداقل یک عضو مجموعهٔ Y جفت‌شده‌باشد،
2. هیچ عضو X نباید با بیش از یک عضو Y جفت‌شده‌باشد،
3. هر عضو مجموعهٔ Y باید با حداقل یک عضو مجموعهٔ X جفت‌شده‌باشد و
4. هیچ عضو Y نباید با بیش از یک عضو X جفت‌شده‌باشد.

شرط‌های یک و دو تضمین می‌کنند که f تابعی با دامنه‌ی X است. شرط‌های یک و دو گاهی به صورت یک شرط هم نوشته می‌شوند: باید هر عضو مجموعهٔ X دقیقاً با یک عضو از مجموعهٔ Y جفت شود. توابعی که شرط سوم را دارا هستند توابع پوشا نام دارند. شرط چهارم هم تعریف توابع یک‌به‌یک است. با توجه به این عبارت می‌توان نتیجه گرفت که یک تابع دوسویی است اگر و فقط اگر هم یک‌به‌یک باشد هم پوشا.

مثال

معلم در کلاس به دانش‌آموزان می‌گوید روی صندلی‌ها بنشینند و مشاهده می‌کند همه دانش‌آموزان نشسته‌اند و تمام صندلی‌ها پر هستند و نتیجه می‌گیرد تعداد دانش‌آموزان و صندلی‌ها برابر است. با بررسی ۴ شرط تعریف می‌توان نتیجه گرفت که با جفت کردن هر دانش‌آموز با صندلیش می‌توان تناظر یک‌به‌یک میان دانش‌آموزان و صندلی‌ها ایجاد کرد:

1. تمام دانش‌آموزان نشسته‌اند (هیچ‌کدام سرپا نیست)،
2. هیچ دانش‌آموزی روی بیش از یک صندلی ننشسته است.
3. تمام صندلی‌ها پر هستند و
4. روی هیچ صندلی بیش از یک نفر ننشسته است.

پس میان دانش‌آموزان وصندلی‌ها تناظر یک‌به‌یک برقرار است و در نتیجه تعداد دانش‌آموزان و صندلی‌ها برابر است.

مثال دیگر بازیکنان فوتبال (یا هر ورزش دیگر) و جایگاه آن‌ها در زمین بازی است. اگر ۱۱ بازیکن و ۱۱ جایگاه در ترکیب تیم در نظر بگیریم با جفت کردن هر بازیکن با جایگاهش تناظر به دست می‌آید. چون ۴ شرط فوق برآورده می‌شوند.

مثال‌های ریاضی توابع دوسویی و توابع غیر دوسویی

• برای هر مجموعه X تابع همانی، دوسویی است.
• تابع f: R → R, f(x) = 2x + ۱ دوسویی است چون برای هر y یک x = (y − ۱)/۲ وجود دارد. به طور کلی تمام توابع خطی به شکل f(x) = ax + b روی اعداد حقیقی دوسویی هستند اگر a مخالف صفر باشد. چون برای هر y وجود دارد یک x = (y - b)/a.
• تابع (f: R → (-π/۲, π/2), f(x) = arctan(x دوسویی هست چون هر x دقیقاً با یک زاویه مثل y در بازهٔ (π/۲, π/۲-) جفت می‌شود به طوری که (y = arctan(x به عبارت دیگر معادلهٔ

(x = tan (y در بازه مذکور دقیقاً یک جواب دارد.

• تابع نمایی g: R → R, g(x) = e^x دو سویی نیست. چون مثلاً هیچ x ای وجود ندارد که g(x)=-۱ پس این تابع پوشا نیست؛ ولی اگر هم‌دامنه را به اعداد مثبت محدود کنیم این تابع پوشا و در نتیجه دوسویی می‌شود و وارون این تابع لگاریتم طبیعی نام دارد.
• تابع h: R → R⁺, h(x) = x²دوسویی نیست چون یک‌به‌یک نیست مثلاً h(−۱) = h(1) = ۱ ولی اگر دامنه آن را به اعداد مثبت محدود کنیم یک‌به‌یک و در نتیجه دوسویی می‌شود و تابع جذر معکوسش است.

معکوس

یک تناظر یک‌به‌یک f با دامنهٔ X (به عبارت دیگر f: X → Y) یک رابطه را هم از Y به X تعریف می‌کند. به دلیل خواص (۳) و (۴) تعریف تابع دوسویی این رابطه یک تابع با دامنه Y هست و به دلیل خواص (۱) و (۲) تعریف این تابع پوشا و یک‌به‌یک هست. پس معکوس تابع دوسویی وجود دارد و دوسویی است. توابعی که معکوس دارند معکوس‌پذیر نامیده می‌شوند. تابع معکوس‌پذیر است اگر و فقط اگر دوسویی باشد.

به عبارت دیگر تابع f: X → Y دوسویی است اگر و فقط اگر به ازای هر y عضو Y وجود دارد x منحصر به فرد عضو X که f(x)=y

با توجه به مثال معلم و دانش‌آموزان اگر تابع را به این صورت تعریف کنیم که نام دانش‌آموز را به عنوان ورودی بگیرد و شمارهٔ صندلی او را به عنوان خروجی بدهد چون دوسویی است معکوس دارد؛ و معکوس آن تابعی است که شمارهٔ صندلی ورودی آن و نام دانش‌آموز خروجی آن است. این تابع هم دوسویی است.

ترکیب

ترکیب دو تابع دوسویی fوg ${\displaystyle \scriptstyle g\,\circ \,f}$ یک تابع دوسویی است. معکوس ${\displaystyle \scriptstyle g\,\circ \,f}$ می‌شود ${\displaystyle \scriptstyle (g\,\circ \,f)^{-1}\;=\;(f^{-1})\,\circ \,(g^{-1})}$.

یک تابع دوسویی که از ترکیب تابع یک‌به‌یک (سمت چپ) و یک تابع پوشا (سمت راست) به دست می‌آید.

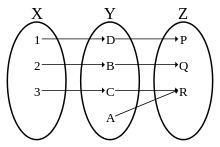
اگر ترکیب دو تابع ${\displaystyle \scriptstyle g\,\circ \,f}$ تابع دوسویی باشد می‌توان نتیجه‌گرفت: f تابع یک‌به‌یک و g تابع پوشا است.

تناظرهای یک‌به‌یک و کاردینالیتی

اگر X و Y مجموعه‌های متناهی باشند میان X و Y تناظر یک‌به‌یک وجود دارد اگر و فقط اگر تعداد اعضای آن‌ها برابر باشد. در واقع در نظریه اصل موضوعی مجموعه‌ها این به عنوان تعریف برابری تعداد اعضا استفاده شده‌است(بنداشت گسترش) یا ([[equinumerosity]])، تعمیم این به مجموعه‌های نامتناهی باعث به‌وجودآمدن مفهوم اعداد کاردینال می‌شود که روشی برای بررسی بی‌نهایت‌ها با اندازه‌های مختلف هستند.

خواص

• یک تابع دوسویی است اگر نمایش آن با هر خط افقی و عمودی دقیقاً در یک نقطه برخورد داشته‌باشد.
• برای یک مجموعه مانند X، مجموعهٔ تمام تناظرها از X به خودش همراه با عملگر ترکیب توابع یک گروه را می‌سازد که نام آن گروه سیمتریک آن مجموعه است؛ و با نمادهای S(X), S_X و !X(فاکتوریل) نشان داده‌می‌شود.
• اگر X و Y مجموعه‌های متناهی با تعداد اعضای برابر باشند و f: X → Y در این صورت گزاره‌های زیر هم ارزند:
  1. f یک‌به‌یک است.
  2. f پوشا است.
  3. f دوسویی است.
• برای هر مجموعه S میان تناظرها از S به خودش و ترتیب‌های کامل اعضا تناظر یک‌به‌یک وجود دارد. به عبارت دیگر تعداد جایگشت‌ها با تعداد ترتیب‌های کامل برابر است که هر دو برابر !n هستند.

تناظرهای یک‌به‌یک و نظریه رده‌ها

در رده از مجموعه‌ها تناظرهای یک‌به‌یک دقیقاً یک‌ریختی‌ها هستند. اگرچه برای رده‌های پیچیده‌تر تناظرهای یک‌به‌یک همواره یک‌ریختی نیستند.

هم چنین ببینید

تابع یک‌به‌یک

تابع پوشا

نظریه رده‌ها

منابع

Bijection