توزیع دیریکله
توزیع دیریکله در نظریه احتمال و آمار یک توزیع پیوسته است. این توزیع بهطور کلی حالت گسترش یافته توزیع بتا برای توابع چندمتغیره است. معمولاً از توزیع دیریکله به عنوان توزیع پیشین در مدل سازی بیزی استفاده میشود؛ چرا که توزیع دیریکله مزدوج پیشین (conjugate prior) برای توزیع چندجمله ای و توزیع دسته ای (categorical) است. تعمیم این توزیع فرایند دیریکله است.
|
تابع چگالی احتمال 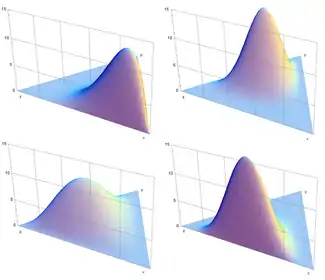 | |||
| فراسنجهها |
تعداد دسته ها (عددی صحیح) concentration parameters, که در آن | ||
|---|---|---|---|
| تکیهگاه | که در آن و | ||
| تابع چگالی احتمال |
که در آن که در آن | ||
| میانگین |
(see digamma function) | ||
| مُد | |||
| واریانس |
که در آن | ||
| آنتروپی | see text | ||

تعریف ریاضی
تابع چگالی احتمال آن به صورت زیر است:
به ازای همهٔ x1, ..., xK–1> 0 بطوریکه x1 + ... + xK–1 < 1, و xK = 1 – x1 – ... – xK–1. چگالی در خارج از این ناحیه صفر است. ثابت نرمالیزاسیون به صورت زیر تعریف میشود:
حالت های خاص
یک حالت خاص زمانی است که تمامی مقادیر مقدار یکسانی داشته باشند، که در اینصورت آن را توزیع دیریکلهٔ متقارن می نامیم. در این حالت توزیع ساده میشود به:
زمانی که توزیع معادل با توزیع یکنواخت روی یک تکیهگاه (ریاضی) سیمپلکس بعدی.
ویژگی ها
گشتاورها
فرض کنیم متغیرهای تصادفی و : را در اختیار داریم. تعریف میکنیم . بنابرین [1][2]
علاوه بر این اگر if
مد
مد توزیع برداری مانند (x1, ..., xK) است که در آن:
توزیع حاشیه ای
توزیعهای حاشیه ای توزیع دیریکله، توزیع بتا هستند.
مزدوج برای توزیع چندجمله ای/دسته ای
این به این معنی است که اگر در مدلسازی مجموعه ای از داده ها از توزیع چندجمله ای/دسته ای استفاده کنیم و توزیع پیشین را دیریکله قرار دهیم، توزیع پسین الزاماً یک توزیع دیریکله خواهد بود. به زبان ریاضی یعنی
بنابرین روابط مقابل برقرار هستند:
ادغام پارامترها
اگر اگر متغیرهای تصادفی i-ام و j-م را با هم ادغام کنیم دیریکلهٔ حاصل برابر است با:
منابع
- Eq. (49.9) on page 488 of Kotz, Balakrishnan & Johnson (2000). Continuous Multivariate Distributions. Volume 1: Models and Applications. New York: Wiley.
- BalakrishV. B. (۲۰۰۵). «"Chapter ۲۷٫ Dirichlet Distribution"». A Primer on Statistical Distributions. Hoboken, NJ: John Wiley & Sons, Inc. ص. ۲۷۴. شابک ۹۷۸-۰-۴۷۱-۴۲۷۹۸-۸.