توزیع گامبل

در نظریه احتمالات و آمار از توزیع گامبل (Gumbel distribution) استفاده می‌شود تا توزیع بیشینه یا کمینهٔ شماری از نمونه‌های توزیع‌های مختلف را مدل کند. برای نمونه اگر فهرستی از ارتفاع بیشینهٔ آب یک رودخانه در ده سال گذشته موجود باشد با استفاده از این توزیع، می‌توان توزیع حد بیشینهٔ آب رودخانه را در یک سال مشخص ارائه کرد.

گامبل

تابع چگالی احتمال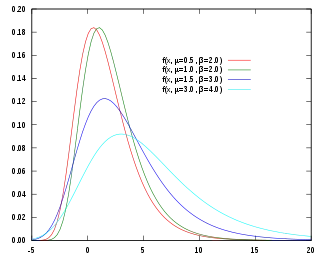
تابع توزیع تجمعی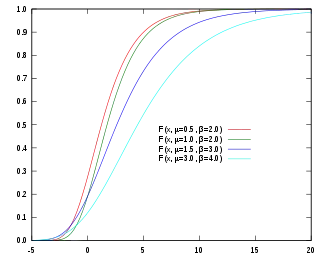
فراسنجه‌ها	${\displaystyle \mu ,}$ پارامتر مکان (عدد حقیقی) ${\displaystyle \beta >0,}$ پارامتر مقیاس (real)
تکیه‌گاه	${\displaystyle \mathbb {R} }$
تابع چگالی احتمال	${\displaystyle {\frac {1}{\beta }}e^{-(z+e^{-z})}}$ که در آن ${\displaystyle z={\frac {x-\mu }{\beta }}}$
تابع توزیع تجمعی	${\displaystyle e^{-e^{-(x-\mu )/\beta }}}$
میانگین	${\displaystyle \mu +\beta \gamma }$ که در آن ${\displaystyle \gamma }$ ثابت اویلر-ماسکرونی است.
میانه	${\displaystyle \mu -\beta \ln(\ln 2)}$
مُد	${\displaystyle \mu }$
واریانس	${\displaystyle {\frac {\pi ^{2}}{6}}\beta ^{2}}$
چولگی	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14}$
کشیدگی	${\displaystyle {\frac {12}{5}}}$
آنتروپی	${\displaystyle \ln(\beta )+\gamma +1}$
تابع مولد گشتاور	${\displaystyle \Gamma (1-\beta t)e^{\mu t}}$
تابع مشخصه	${\displaystyle \Gamma (1-i\beta t)e^{i\mu t}}$

توزیع گامبل حالت خاصی از توزیع مقدار حدی تعمیم‌یافته است.

ویژگی‌ها

تابع توزیع تجمعی توزیع گامبل عبارت است از:

${\displaystyle F(x;\mu ,\beta )=e^{-e^{-(x-\mu )/\beta }}.\,}$

اگر مد را μ و میانه را ${\displaystyle \mu -\beta \ln \left(\ln 2\right),}$ بنامیم، میانگین چنین خواهد بود:

${\displaystyle \operatorname {E} (X)=\mu +\gamma \beta ,}$

که در آن ${\displaystyle \gamma \approx 0.5772}$، ثابت اویلر-ماسکرونی است.

انحراف معیار ${\displaystyle \sigma }$ برابر خواهد بود با ${\displaystyle \beta \pi /{\sqrt {6}}}$ در نتیجه ${\displaystyle \beta =\sigma {\sqrt {6}}/\pi \approx 0.78\sigma .}$ [1]

در حالتی که ${\displaystyle x=\mu }$ است مقدار ${\displaystyle F(x;\mu ,\beta )}$ به ازای ${\displaystyle \beta .}$ دلخواه برابر با ${\displaystyle e^{-1}\approx 0.37}$ می‌شود.

حالت استاندارد توزیع گامبل هنگامی است که ${\displaystyle \mu =0}$ و ${\displaystyle \beta =1}$ باشد و تابع توزیع تجمعی به صورت زیر باشد:

${\displaystyle F(x)=e^{-e^{(-x)}}\,}$

همچنین تابع چگالی احتمالات به صورت زیر باشد:

${\displaystyle f(x)=e^{-(x+e^{-x})}.}$

در این حالت، مد برابر با صفر و میانه ${\displaystyle -\ln(\ln(2))\approx 0.3665}$ خواهد شد. میانگین ${\displaystyle \gamma }$ است و انحراف معیار ${\displaystyle \pi /{\sqrt {6}}\approx 1.2825.}$ است.

انباشتک‌ها برای n>1 عبارت است از:

${\displaystyle \kappa _{n}=(n-1)!\zeta (n).}$

منابع

1. Oosterbaan, R.J. (1994). "Chapter 6 Frequency and Regression Analysis". In Ritzema, H.P. Drainage Principles and Applications, Publication 16 (PDF). Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). pp. 175–224. ISBN 90-70754-33-9.