توزیع پارتو

توزیع پارتو (به انگلیسی: Pareto distribution) نوعی توزیع احتمال قانون-توانی است، که در توصیف پدیده‌های قابل مشاهده، از نوع اجتماعی، علمی، ژئوفیزیکی، و بیم‌سنجی و بسیاری موارد دیگر استفاده می‌شود. این توزیع در اصل برای توصیف توزیع ثروت در یک جامعه استفاده شده بود، و با این گرایش توزیع ثروت که «بخش زیادی از ثروت توسط بخش اندکی از جمعیت نگهداری می‌شود»، هماهنگ است.[1] به صورت محاوره‌ای به این توزیع «اصل پارتو» یا «قاعده ۸۰–۲۰» هم می‌گویند، همچنین گاهی به آن «اصل میتو» گفته می‌شود. این قاعده می‌گوید: برای مثال، «۸۰ درصد از ثروت یک جامعه توسط ۲۰ درصد از جمعیت آن نگهداری می‌شود». با این حال، نباید توزیع پارتو را با اصل پارتو یکسان دانست، زیرا توزیع پارتو فقط برای مقدار ${\displaystyle \alpha }$ خاصی این نتیجه را تولید می‌کند (α = log₄5 ≈ ۱٫۱۶). با اینکه ${\displaystyle \alpha }$ یک پراسنجه است، مشاهدات تجربی نشان داده‌اند که توزیع ۸۰–۲۰، هماهنگی خوبی با نمونه‌های متنوع و گسترده دارد، که این نمونه‌ها از نوع پدیده‌های طبیعی[2] و فعالیت‌های انسانی[3] می‌باشند.

توزیع پارتو نوع I

تابع چگالی احتمال 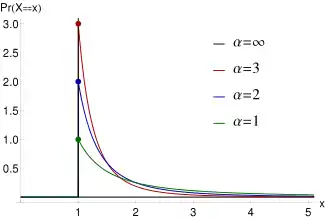تابع توزیع احتمالی پارتو برای مقادیر مختلف ${\displaystyle \alpha }$ و ${\displaystyle x_{\mathrm {m} }=1}$. وقتی که حد k به بی‌نهایت میل می‌کند تابع توزیع احتمالی به (δ(x − xm میل می‌کند که δ تابع دلتای دیراک می‌باشد.
تابع توزیع تجمعی 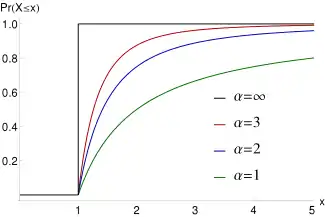تابع توزیع تجمعی پارتو برای مقادیر مختلف ${\displaystyle \alpha }$ و ${\displaystyle x_{\mathrm {m} }=1}$.
فراسنجه‌ها	${\displaystyle x_{\mathrm {m} }>0\,}$ مکان (حقیقی) شکل (حقیقی) ${\displaystyle k>0\,}$
تکیه‌گاه	${\displaystyle x\in [x_{\mathrm {m} };+\infty )\!}$
تابع چگالی احتمال	${\displaystyle {\frac {k\,x_{\mathrm {m} }^{k}}{x^{k+1}}}\!}$
تابع توزیع تجمعی	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{k}\!}$
میانگین	${\displaystyle {\frac {k\,x_{\mathrm {m} }}{k-1}}\!}$ for ${\displaystyle k>1}$
میانه	${\displaystyle x_{\mathrm {m} }{\sqrt[{k}]{2}}}$
مُد	${\displaystyle x_{\mathrm {m} }\,}$
واریانس	${\displaystyle {\frac {x_{\mathrm {m} }^{2}k}{(k-1)^{2}(k-2)}}\!}$ for ${\displaystyle k>2}$
چولگی	${\displaystyle {\frac {2(1+k)}{k-3}}\,{\sqrt {\frac {k-2}{k}}}\!}$ for ${\displaystyle k>3}$
کشیدگی	${\displaystyle {\frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}\!}$ for ${\displaystyle k>4}$
آنتروپی	${\displaystyle \ln \left({\frac {k}{x_{\mathrm {m} }}}\right)-{\frac {1}{k}}-1\!}$
تابع مولد گشتاور	تعریف نشده
تابع مشخصه	${\displaystyle k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t)\,}$
اطلاع فیشر	${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha }{x_{\mathrm {m} }^{2}}}&-{\dfrac {1}{x_{\mathrm {m} }}}\\-{\dfrac {1}{x_{\mathrm {m} }}}&{\dfrac {1}{\alpha ^{2}}}\end{bmatrix}}}$ Right: ${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha ^{2}}{x_{\mathrm {m} }^{2}}}&0\\0&{\dfrac {1}{\alpha ^{2}}}\end{bmatrix}}}$

توزیع پارتو از نام مهندس عمران، اقتصاددان و جامعه‌شناس ایتالیایی، ویلفردو پارتو گرفته شده است. واژه Pareto در انگلیسی به صورت «پِرِیتو» (US: ‎/pəˈreɪtoʊ/‎ pə-RAY-toh) تلفظ می‌شود.

تاریخچه

در سال ۱۸۹۷، اقتصاددان ایتالیایی ویلفردوپارتو (۱۹۲۳–۱۸۴۸) که شاگرد لئون والراس بود و پس از او به احراز کرسی اقتصاد سیاسی دانشگاه لوزان دست یافت، باعث ایجاد نظم خاصی در توزیع درآمدها در کشورهای سرمایه‌داری و نیز کشورهایی که در شرایط فئودالی و سرمایه‌داری اولیه بودند شد. پارتو قصد داشت براساس این قانون نتایجی با ماهیت اقتصادی و اجتماعی به‌دست‌آورد.

پارتو دومین نفر از مکتب لوزان است؛ مکتب لوزان توسط لئون والراس (۱۸۳۴–۱۹۱۰) پایه‌گذاری شد؛ این مکتب علاوه بر بحث دربارهٔ مقوله مطلوبیت، به هزینه و عرضه نیز پرداخته‌است؛ با این بیان که اگر قیمت، بالاتر از هزینه تولید قرار گیرد، عرضه افزایش پیدا می‌کند تا قیمت را پایین آورد و بالعکس؛ اگر هزینه از قیمت پیشی گیرد، عرضه کاهش پیدا کرده و قیمت‌ها بالا می‌روند. پارتو یکی از بنیانگذاران اقتصاد ریاضی نیز شناخته شده‌است. دیدگاه او در مقوله تعادل عمومی در اقتصاد رفاه، جایگاه اساسی دارد.

پارتو بر مبنای آمارهای کشورهای مختلف، توزیع‌های فراوانی بدست آورد که معرف تعداد افرادی بودند که درآمدشان برابر مقداری معین یا بیشبر از آن بود. آنگاه نمودارهای این توزیع‌های فراوانی را رسم کرد. محور افقی این نمودارها معرف درآمد و محور عمودی، تعداد افراد با درآمد x یا بیشتر را نشان می‌داد.

پارتو دریافت که دراغلب حالات مورد بررسی، منحنی‌های نشان دهندهٔ این نوع توزیع‌های درآمد شکلی مشابه دارند. یعنی منحنی‌هایی هستند که معادله آنها با فرمول زیر مشخص می‌شود:

${\textstyle y={A \over (x-b)^{b}}}$

که در آنها b کمترین حد درآمدی است که منحنی از آن شروع می‌شود، درحالی که A, پارامترهای معین مثبت هستند. نمودار این منحنی، منحنی پارتو نام دارد.[4]

تعریف

تابع چگالی احتمال

تابع چگالی احتمال یک توزیع پارتو چنین است.

${\displaystyle f_{X}(x)={\begin{cases}{\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}\qquad \alpha >0}$

ویژگی‌ها

تابع توزیع تجمعی

تابع توزیع تجمعی در توزیع پارتو برابر است با:

${\displaystyle F_{X}(x)={\begin{cases}1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}\qquad \alpha >0}$

و همچنین معکوس آن برابر است با:

${\displaystyle F^{-1}(\rho )={x_{m} \over (1-\rho )^{1 \over \alpha }}\qquad 0\leq \rho <1}$

میانه

میانه در توزیع پارتو برابر است با:

${\displaystyle M={\sqrt[{\alpha }]{2}}x_{m}}$

مد

مد در توزیع پارتو برابر است با:

${\displaystyle \mod =x_{m}}$

امید ریاضی

امید ریاضی یک توزیع پارتو برابر است با:

${\displaystyle \operatorname {E} (X)={\begin{cases}\infty &\alpha \leq 1,\\{\frac {\alpha x_{\mathrm {m} }}{\alpha -1}}&\alpha >1.\end{cases}}}$

${\displaystyle \operatorname {E} (X^{2})={\begin{cases}\infty &\alpha \leq 2,\\{\frac {\alpha {x_{m}}^{2}}{\alpha -2}}&\alpha >2.\end{cases}}}$

${\displaystyle \operatorname {E} (X^{n})={\begin{cases}\infty &\alpha \leq n,\\{\frac {\alpha {x_{m}}^{n}}{\alpha -n}}&\alpha >n.\end{cases}}}$

واریانس

واریانس یک توزیع پارتو برابر است با:

${\displaystyle \operatorname {Var} (X)={\begin{cases}\infty &\alpha \in (1,2],\\\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}&\alpha >2.\end{cases}}}$

برای ${\displaystyle \alpha <2}$واریانس تعریف نشده‌است.

انحراف معیار

انحراف معیار یک توزیع پارتو برابر است با:

${\displaystyle \operatorname {\sigma } (X)={\begin{cases}\infty &\alpha \in (1,2],\\\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right){\sqrt {\frac {\alpha }{\alpha -2}}}&\alpha >2.\end{cases}}}$

توزیع پارتو تعمیم‌یافته

۵ نوع توزیع تعمیم یافته وجود دارد که توزیع پارتو را تعمیم می‌دهد.[5][6]

توزیع‌های پارتو

	${\displaystyle F(x)}$	شرایط		${\displaystyle \operatorname {E} [X]}$		${\displaystyle \operatorname {E} [X^{\delta }]}$
نوع ۱	${\displaystyle 1-\left[{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \sigma }$	${\displaystyle \sigma >0,\alpha }$	${\displaystyle {\frac {\sigma \alpha }{\alpha -1}}}$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\alpha }{\alpha -\delta }}}$	${\displaystyle \delta <\alpha }$
نوع ۲	${\displaystyle 1-\left[1+{\frac {x-\mu }{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma >0,\alpha }$	${\displaystyle {\frac {\sigma \alpha }{\alpha -1}}}$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\delta )\Gamma (1+\delta )}{\Gamma (\alpha )}}}$	${\displaystyle -1<\delta <\alpha }$
نوع Lomax	${\displaystyle 1-\left[1+{\frac {x-\mu }{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq 0}$	${\displaystyle \sigma >0,\alpha }$
نوع ۳	${\displaystyle 1-\left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-1}}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0}$	${\displaystyle \sigma \Gamma (1-\gamma )\Gamma (1+\gamma )}$	${\displaystyle -1<\gamma <1}$	${\displaystyle \sigma ^{\delta }\Gamma (1-\gamma \delta )\Gamma (1+\gamma \delta )}$	${\displaystyle -\gamma ^{-1}<\delta <\gamma ^{-1}}$
نوع ۴	${\displaystyle 1-\left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0,\alpha }$	${\displaystyle {\frac {\sigma \Gamma (\alpha -\gamma )\Gamma (1+\gamma )}{\Gamma (\alpha )}}}$	${\displaystyle -1<\gamma <\alpha }$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\gamma \delta )\Gamma (1+\gamma \delta )}{\Gamma (\alpha )}}}$	${\displaystyle -\gamma ^{-1}<\delta <\alpha /\gamma }$

${\displaystyle P(IV)(\sigma ,\sigma ,1,\alpha )=P(I)(\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,\gamma ,1)=P(III)(\mu ,\sigma ,\gamma ).}$

کاربردها

اصل پارتو

پارتو در ابتدا از این توزیع برای توصیف تخصیص ثروت در میان افراد استفاده می‌کرد، زیرا به نظر می‌رسید که بخش بزرگی از ثروت هر جامعه متعلق به درصد کمتر از مردم در آن جامعه است. او همچنین برای توصیف توزیع درآمد از آن استفاده کرد.[7] این ایده گاهی به سادگی به عنوان اصل پارتو یا "حکم ۸۰–۲۰" بیان می‌شود که می‌گوید ۲۰ درصد از جمعیت ۸۰ درصد ثروت را کنترل می‌کنند.[8] با این وجود، قواعد ۸۰–۲۰ به ارزش خاص ${\displaystyle \alpha }$ مربوط می‌شود و در واقع، اطلاعات پارتو دربارهٔ مالیات بر درآمد بریتانیا در سیاست‌های اقتصادی خود نشان می‌دهد که حدود ۳۰ درصد از جمعیت حدود ۷۰ درصد درآمد داشته‌است. نمودار تابع چگالی احتمال (PDF) نشان می‌دهد که احتمال یا کسری از جمعیت که دارای مقدار کمی ثروت در هر فرد است نسبتاً بالا است و پس از آن به‌طور ثابتی به عنوان افزایش ثروت کاهش می‌یابد. (توجه داشته باشید که توزیع پارتو برای ثروت برای انتهای پایین واقع‌گرایانه نیست. در حقیقت، ارزش خالص ممکن است حتی منفی باشد).

«انجام هر کدام از کارهای موجود در لیست شما ممکن است به یک اندازه وقت شما را بگیرد ولی انجام یک یا دو تای آنها چند برابر هر یک از سایر موارد برای شما سودمند خواهد بود. گاهی پیش می‌آید که ارزش یکی از ده کار یا فعالیتی که شما در لیست خود دارید به تنهایی می‌تواند بیش از مجموع سایر فعالیت‌ها در موفقیت شما ارزشمند باشد. این کار بی تردید همان قورباغه ای است که باید اول از همه قورت بدهید. می‌توانید حدس بزنید که یک فرد معمولی احتمالاً در انجام چه کارهایی بیشتر تنبلی می‌کند؟ واقعیت تاسف بار این است که اکثر مردم در مورد انجام همان ده یا بیست درصد از فعالیت‌هایی که در صدر قرار دارند و بیشترین ارزش و اهمیت را دارند تنبلی می‌کنند یعنی در مورد همان اقلیت بسیار مهم. در عوض وقت خود را صرف هشتاد درصد فعالیت‌هایی می‌کنند که در موفقیت آنها اهمیت بسیار کمی دارد و تأثیر ناچیزی در دست یابی به نتایج ارزشمند می‌گذارد. یعنی همان اکثریت کم‌اهمیت.»[9]

دیگر کاربردهای آن

بسیاری از پدیده‌های اجتماعی، علمی و ژئوفیزیکی توسط توزیع پارتو توصیف می‌شوند. این توزیع در مباحث طول عمر و قابلیت اعتماد دارای اهمیت فراوان است.

از دیگر کاربردهای آن می‌توان به موارد زیر اشاره کرد:

• اندازه شهرک‌های انسانی (چند شهر بزرگ دربرابر بسیاری از شهرهای کوچک و روستاها)[10]
• توزیع حجم فایل ترافیک اینترنتی که از پروتکل TCP استفاده می‌کند (چند عدد بزرگ دربرابر بسیاری از عددهای کوچک)[10]
• نرخ خطا در هارد دیسک[11]
• خوشه‌های معادله بوز-اینشتین نزدیک صفر مطلق
• ارزش ذخایر نفت در میدان‌های نفتی (چند میدان بزرگ دربرابر بسیاری از میدان‌های کوچک)[10]
• توزیع طولی در مشاغل سوپر کامپیوترها (چند عدد بزرگ دربرابر بسیاری از عددهای کوچک)
• قیمت استاندارد شده بر روی سهام فردی[10]
• اندازه ذرات شن و ماسه[10]
• اندازه شهاب سنگ‌ها
• بارندگی سالانه حداکثر یک روزه و تخلیه رودخانه[12]

نمونه‌ای از توزیع پارتو

درآمد یک جمعیت خاص

فرض کنید که درآمد یک جمعیت خاص دارای توزیع پارتو با ${\displaystyle \alpha =3}$ و ${\displaystyle x_{m}=1000}$ است.[13]

حال می‌خواهیم نسبت جمعیت افراد با درآمد ۲۰۰۰ تا ۴۰۰۰ را بدست آوریم.

${\displaystyle \int _{2000}^{4000}{{3*1000^{3} \over x^{4}}dx}={1000^{3} \over 2000^{3}}-{1000^{3} \over 4000^{3}}=0.109375}$

حال می‌خواهیم درآمد آن‌ها را بدست آوریم.

${\displaystyle \int _{2000}^{4000}{{3*1000^{3} \over x^{4}}x\,dx}={3*1000 \over 2}[({1000 \over 2000})^{2}-({1000 \over 4000})^{2}]=281.25}$

درآمد کل نیز برابر است با:

${\displaystyle \int _{1000}^{\infty }{{3*1000^{3} \over x^{4}}x\,dx}={3*1000 \over 2}=1500}$

بنابراین ۱۰٫۹۳۷۵ درصد افراد دارای درآمدی بین ۲۰۰۰ تا ۴۰۰۰ هستند که ۱۸٫۷۵ درصد درآمد کل را دارند.

کد در زبان R

library("EnvStats") # Package for Environmental Statistics

pareto <- rpareto(n = 10000000, location = 1000, shape = 3) # Get 10000000 numbers of Pareto distribution
pareto <- pareto[pareto > 1000] # Get numbers greater than 1000
number <- 0 # Number of people with income from 2000 to 4000

for (i in pareto) {
  if (i <= 4000 && i >= 2000) {
    number = number + 1
  }
}
cat("proportion of people with income from 2000 to 4000:", number / length(pareto))

paretoPlot <- pareto[pareto < 5000] # Get numbers less than 5,000 to draw charts
hist(paretoPlot, breaks = 150) # Draw charts

منابع

1. Pareto, Vilfredo (1898). "Cours d'economie politique". Journal of Political Economy. 6.
2. VAN MONTFORT, M.A.J. (1986). "The Generalized Pareto distribution applied to rainfall depths". Hydrological Sciences Journal. 31 (2): 151–162. doi:10.1080/02626668609491037.
3. Oancea, Bogdan (2017). "Income inequality in Romania: The exponential-Pareto distribution". Physica A: Statistical Mechanics and Its Applications. 469: 486–498. Bibcode:2017PhyA..469..486O. doi:10.1016/j.physa.2016.11.094.
4. «پایان‌نامه تحصیلی دورهٔ کارشناسی ارشد». رضا پورطاهری. شهریور 70. تاریخ وارد شده در |تاریخ= را بررسی کنید (کمک)
5. B.، Douglas, J. (۱۹۸۰). Analysis with standard contagious distributions. Fairland, Md.: International Co-operative Pub. House. OCLC 7792137. شابک ۰۸۹۹۷۴۰۱۲X.
6. Kotz، Samuel, ویراستار (۲۰۰۴-۰۷-۱۵). Encyclopedia of Statistical Sciences. Hoboken, NJ, USA: John Wiley & Sons, Inc. شابک ۰۴۷۱۶۶۷۱۹۶.
7. Pareto، Vilfredo (۱۹۶۴). Cours d'économie politique. Librairie Droz. شابک ۹۷۸۲۶۰۰۰۴۰۱۴۳.
8. Notestein, Frank W. (1974-01). "The World Population Year". Population Index. 40 (1): 18. doi:10.2307/2733536. ISSN 0032-4701. Check date values in: |date= (help)
9. Sardana, G.D. (2007-07). "Eat That Frog! Brian Tracy". Paradigm. 11 (2): 83–84. doi:10.1177/0971890720070213. ISSN 0971-8907. Check date values in: |date= (help)
10. Reed, William J.; Jorgensen, Murray (2004-12-31). "The Double Pareto-Lognormal Distribution—A New Parametric Model for Size Distributions". Communications in Statistics - Theory and Methods. 33 (8): 1733–1753. doi:10.1081/sta-120037438. ISSN 0361-0926.
11. Schroeder, Bianca; Damouras, Sotirios; Gill, Phillipa (2010-09-01). "Understanding latent sector errors and how to protect against them". ACM Transactions on Storage. 6 (3): 1–23. doi:10.1145/1837915.1837917. ISSN 1553-3077.
12. Random Variables and Cumulative Distribution. 1000 20th Street, Bellingham, WA 98227-0010 USA: SPIE. صص. ۳–۳. شابک ۹۷۸۰۸۱۹۴۸۷۰۱۸.
13. "AP Statistics Curriculum 2007 Pareto - Socr". wiki.stat.ucla.edu. Retrieved 2018-10-29.

• مشارکت‌کنندگان ویکی‌پدیا. «Pareto distribution». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۹ می ۲۰۱۱.