توزیع فوق‌هندسی

توزیع فوقِ‌هندسی[1] (به انگلیسی: Hypergeometric distribution) مجموعه ای از N عضو را در نظر بگیرید که k عضو آن دارای یک ویژگی و بقیه، فاقد این ویژگی هستند. مانند 500 لامپ موجود در یک جعبه که 300 تای آن سالم و بقیه معیوب باشند. حال فرض کنید می خواهیم از این مجموعه، n عضو به صورت تصادفی (بدون جایگذاری) انتخاب کنیم. دراین صورت اگر متغیر تصادفیX تعداد عناصری در n برداشت باشد که دارای ویژگی موردنظر هستند، می گوئیم X دارای توزیع فوق هندسی است.

فوقِ هندسی

تابع جرم احتمال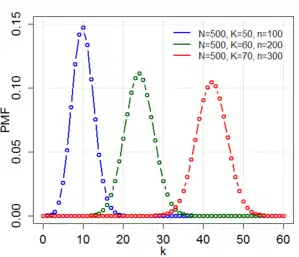
تابع توزیع تجمعی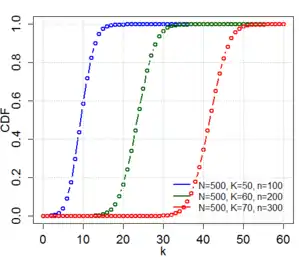
فراسنجه‌ها	${\displaystyle {\begin{aligned}N&\in \left\{0,1,2,\dots \right\}\\K&\in \left\{0,1,2,\dots ,N\right\}\\n&\in \left\{0,1,2,\dots ,N\right\}\end{aligned}}\,}$
تکیه‌گاه	${\displaystyle \scriptstyle {k\,\in \,\left\{\max {(0,\,n+K-N)},\,\dots ,\,\min {(n,\,K)}\right\}}\,}$
تابع جرم احتمال	${\displaystyle {{{K \choose k}{{N-K} \choose {n-k}}} \over {N \choose n}}}$
تابع توزیع تجمعی	${\displaystyle 1-{{{n \choose {k+1}}{{N-n} \choose {K-k-1}}} \over {N \choose K}}\,_{3}F_{2}\!\!\left[{\begin{array}{c}1,\ k+1-K,\ k+1-n\\k+2,\ N+k+2-K-n\end{array}};1\right],}$ که در آن ${\displaystyle \,_{p}F_{q}}$ همان تابع فوق‌هندسی همگانی است.
میانگین	${\displaystyle n{K \over N}}$
مُد	${\displaystyle \left\lceil {\frac {(n+1)(K+1)}{N+2}}\right\rceil -1,\left\lfloor {\frac {(n+1)(K+1)}{N+2}}\right\rfloor }$
واریانس	${\displaystyle n{K \over N}{(N-K) \over N}{N-n \over N-1}}$
چولگی	${\displaystyle {\frac {(N-2K)(N-1)^{\frac {1}{2}}(N-2n)}{[nK(N-K)(N-n)]^{\frac {1}{2}}(N-2)}}}$
کشیدگی	${\displaystyle \left.{\frac {1}{nK(N-K)(N-n)(N-2)(N-3)}}\cdot \right.}$ ${\displaystyle {\Big [}(N-1)N^{2}{\Big (}N(N+1)-6K(N-K)-6n(N-n){\Big )}+{}}$ ${\displaystyle {}+6nK(N-K)(N-n)(5N-6){\Big ]}}$
تابع مولد گشتاور	${\displaystyle {\frac {{N-K \choose n}\scriptstyle {\,_{2}F_{1}(-n,-K;N-K-n+1;e^{t})}}{N \choose n}}\,\!}$
تابع مشخصه	${\displaystyle {\frac {{N-K \choose n}\scriptstyle {\,_{2}F_{1}(-n,-K;N-K-n+1;e^{it})}}{N \choose n}}}$

تعریف

ابتدا برای درک بهتر این توزیع یک مثال مطرح می‌کنیم. فرض کنید از جعبه‌ای شامل D فیوز معیوب و N-D فیوز سالم، n فیوز را به‌طور تصادفی و بدون‌جایگذاری انتخاب‌کنیم. به‌علاوه فرض‌کنیدn، تعداد فیوزهای استخراجی از تعداد فیوزهای معیوب و فیوزهای سالم تجاوز نکند.فرض‌کنید متغیرتصادفی X تعداد فیوزهای معیوب خارج شده باشد.بنابراین:
تعریف: فرض کنید D,N و n اعداد صحیح و مثبت‌اند، با ${\displaystyle n\leq min(D,N-D)}$. دراینصورت،

${\displaystyle p(k)=P(X=k)={{{D \choose k}{{N-D} \choose {n-k}}} \over {N \choose n}}\quad \quad \quad for\quad k\in {0,1,2,...,n}}$

را تابع جرم‌احتمال توزیع فوق‌هندسی می‌گویند.

اثبات ترکیبیاتی تابع احتمال بودن

با استفاده از اتحاد ترکیبیاتی واندرموند به راحتی می‌توان نتیجه‌گرفت که

${\displaystyle \sum _{k=0}^{n}{{{D \choose k}{{N-D} \choose {n-k}}}={N \choose n}}}$

که با استفاده از آن برای همه‌ی مقادیر k به‌سادگی می‌توان ${\displaystyle \sum _{k=0}^{n}p(k)=1}$ را نتیجه‌گرفت.

متوسط و واریانس متغیرتصادفی فوق‌هندسی

برای متغیرتصادفی فوق‌هندسی X که در بالا تعریف شد داریم:

${\displaystyle \operatorname {E} [X]={\frac {nD}{N}}}$

${\displaystyle \operatorname {Var} [X]={\frac {nD(N-D)}{N^{2}}}(1-{\frac {n-1}{N-1}}).}$

توجه‌کنید که اگر آزمایش ستخراج n قلم کالا از جعبه‌ای شامل D قلم کالای معیوب و N-D قلم کالای سالم را با جایگذاری انجام‌دهیم، دراینصورت X دارای توزیع دوجمله‌ای با پارامترهای n و${\displaystyle D \over N}$ است. پس:

${\displaystyle \operatorname {E} [X]={\frac {nD}{N}}}$

${\displaystyle \operatorname {Var} [X]=n{\frac {D}{N}}(1-{\frac {D}{N}})={\frac {nD(N-D)}{N^{2}}}.}$

اینها نشان‌می‌دهند که اگر اقلام با جایگذاری انتخاب شوند، دراینصورت امیدریاضی X تغییر نمی‌کند اما واریانس X افزایش پیدامی‌کند. با وجود این اگر n بسیار کوچکتر از N باشد دراینصورت باتوجه به فرمول واریانس، استخراج باجایگذاری تقریب خوبی برای استخراج بدون‌جایگذاری است.

مثال

در یک کیسه 24 مهره وجود دارد که 4 تای آن قرمز و مابقی سفید هستند. اگر از این کیسه 6 مهره به تصادف و بدون جایگذاری برداریم وX تعداد مهره‌های قرمز باشد؛ توزیع احتمال X را به دست آورید. احتمال اینکه هیچ مهره قرمزی بدست نیاید چقدر است؟ داریم n=6 ,D=4 , N=24 بنابراین توزیع احتمال X فوق هندسی و به صورت زیر است:

${\displaystyle p(k)={{{4 \choose k}{{20} \choose {6-k}}} \over {24 \choose 6}}\quad \quad \quad k\in {0,1,2,3,4}}$

در نتیجه احتمال اینکه هیچ مهره‌ای قرمز نباشد می‌شود:

${\displaystyle p(0)={{{4 \choose 0}{{20} \choose {6}}} \over {24 \choose 6}}=0.288}$

منابع

1. «توزیع فوقِ‌هندسی» [آمار] هم‌ارزِ «hypergeometric distribution»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر یازدهم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۶۰۰-۶۱۴۳-۴۵-۳ (ذیل سرواژهٔ توزیع فوقِ‌هندسی)

• saeed_ghahramani، Fundumentals_of_Probability_3rd.Edition