توزیع پواسون

در آمار و احتمال توزیع پواسون (به انگلیسی: Poisson distribution، ‎/ˈpwɑːsɒn/‎) (یا قانون پواسون اعداد کوچک) یک توزیع احتمالی گسسته است که احتمال اینکه یک حادثه به تعداد مشخصی در فاصلهٔ زمانی یا مکانی ثابتی رخ دهد را شرح می‌دهد؛ به شرط اینکه این حوادث با نرخ میانگین مشخصی و مستقل از زمان آخرین حادثه رخ دهند. (توزیع پواسون همچنین برای تعدادی از حوادث در فاصله‌های مشخص دیگری مثل مسافت، مساحت یا حجم استفاده شود) این توزیع برای اولین بار توسط Siméon Denis Poisson 1781-1840 معرفی و به ضمیمه تئوری احتمال او در سال ۱۸۳۸ در یکی از کتاب‌هایش بنامRecherches sur la probabilité des jugements en matière criminelle et en matière civile(جستاری در احتمال قضاوت‌ها در مسائل کیفری و حقوقی) چاپ شد. اولین استفادهٔ عملی از این توزیع به سال ۱۸۹۸ برمی گردد جایی که Ladislaus Bortkiewicz به بررسی تعداد تصادفی از سربازان ارتش پروس که توسط پا زدن اسب کشته شدند می‌پردازد. این اثر بیشتر بر متغیرهای تصادفی خاصی تأکید می‌کند مانند متغیر تصادفی N که تعداد ظهورها (یا ورودهای) گسسته را که در فاصله زمانی مشخصی اتفاق می‌افتند را می‌شمارد. توزیع پواسن در هر زمینه‌ای استفاده می‌شود برای مثال: فرض کنید شخصی به‌طور متوسط چهار ایمیل در روز دریافت می‌کند تعداد ایمیل‌های دریافت شده در برخی از روزها می‌تواند کمی کمتر یا بیشتر از چهار باشد ولی در بازه زمانی طولانی اگر بر دریافت ایمیل نظارت کنیم، می‌بینیم نرخ دریافت ثابت است. حال فرض کنید فرایند یا ترکیبی از چند فرایند یک جریان رویداد به صورت تصادفی تولید کنند، توزیع پواسن احتمال اینکه تعداد این رخدادها ۲٬۳٬۴ و اعداد دیگر باشد را مشخص می‌کند. توزیع پواسن درجه پراکندگی اطراف نرخ متوسط وقوع رخداد را پیش‌بینی می‌کند.

• در سیستم‌های الکتریکی: تعداد دفعاتی که زنگ یک تلفن به صدا در می‌آید
• در نجوم: فوتون‌هایی که به تلسکوپ می‌رسند
• در صنعت: تعداد محصولات معیوب یک کارخانه
• در فیزیک: تعداد ذرات؛ alpha انتشار یافته در یک ثانیه
• در زیست‌شناسی: تعداد جهش‌ها روی یک رشتهٔ معین از DNA دارای توزیع پواسن است.

توزیع پواسون

تابع جرم احتمال 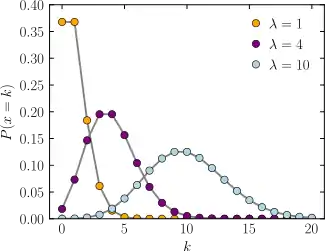محور افقی اندیس k می‌باشد، که معادل تعداد رخداد است. λ معادل نرخ چشمداشتی برای رخدادها است. محور عمودی احتمال k رخداد موقعی است که λ را از قبل بدانیم. این تابع فقط در مقادیر صحیح k تعریف شده‌است. خطوط متصل کننده تنها به دید بهتر کمک می‌کنند.
تابع توزیع تجمعی 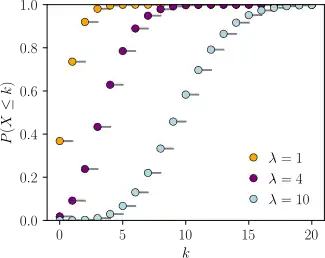محور افقی اندیس k است، که معادل تعداد رخداد است. CDF در مقادیر صحیح k غیرپیوسته است، و در بقیه جاها صاف است، زیرا یک متغیر تصادفی که توسط پواسن توزیع شده است، تنها مقادیر صحیح را می‌پذیرد.
نماد	${\displaystyle \operatorname {Pois} (\lambda )}$
فراسنجه‌ها	${\displaystyle \lambda \in (0,\infty )}$ (نرخ رخداد)
تکیه‌گاه	${\displaystyle k\in \mathbb {N} _{0}}$ (اعداد طبیعی از صفر شروع می شوند)
تابع جرم احتمال	${\displaystyle {\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$
تابع توزیع تجمعی	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor$ !}}} ، یا ${\displaystyle e^{-\lambda }\sum _{i=0}^{\lfloor k\rfloor }{\frac {\lambda ^{i}}{i!}}\ }$، یا ${\displaystyle Q(\lfloor k+1\rfloor ,\lambda )}$ برای ${\displaystyle k\geq 0}$، که در آن ${\displaystyle \Gamma (x,y)}$ برابر تابع گامای ناکامل بالایی، ${\displaystyle \lfloor k\rfloor }$ برابر تابع کف است، و Q معادل تابع گامای منظم‌شده است.
میانگین	${\displaystyle \lambda }$
میانه	${\displaystyle \approx \lfloor \lambda +1/3-0.02/\lambda \rfloor }$
مُد	${\displaystyle \lceil \lambda \rceil -1,\lfloor \lambda \rfloor }$
واریانس	${\displaystyle \lambda }$
چولگی	${\displaystyle \lambda ^{-1/2}}$
کشیدگی	${\displaystyle \lambda ^{-1}}$
آنتروپی	${\displaystyle \lambda [1-\log(\lambda )]+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}$ (برای ${\displaystyle \lambda }$ های بزرگ) ${\displaystyle {\frac {1}{2}}\log(2\pi e\lambda )-{\frac {1}{12\lambda }}-{\frac {1}{24\lambda ^{2}}}-{}}$ ${\displaystyle \qquad {\frac {19}{360\lambda ^{3}}}+O\left({\frac {1}{\lambda ^{4}}}\right)}$
تابع مولد گشتاور	${\displaystyle \exp[\lambda (e^{t}-1)]}$
تابع مشخصه	${\displaystyle \exp[\lambda (e^{it}-1)]}$
تابع مولد احتمال	${\displaystyle \exp[\lambda (z-1)]}$
اطلاع فیشر	${\displaystyle {\frac {1}{\lambda }}}$

اگر امید ریاضی ظهورها در این بازه λ باشد، احتمال اینکه دقیقاً k ظهور داشته باشیم (k عدد صحیح نامنفی است، k=۰، ۱، ۲، …) برابر است با:

${\displaystyle f(k;\lambda )={\frac {\lambda ^{k}e^{-\lambda }}{k!}},\,\!}$

بطوریکه

• e پایه لگاریتم طبیعی است (e=۲٫۷۱۸۲۸)
• k تعداد ظهورهای یک حادثه است که احتمالش با تابع فوق داده شده‌است.
• λ یک عدد مثبت حقیقی و برابر با امید ریاضی ظهورها در طول بازه داده شده‌است. برای مثال اگر به‌طور میانگین در هر دقیقه ۴ حادثه اتفاق بیفتد و احتمال اتفاق افتادن یک حادثه در فاصله زمانی ۱۰ دقیقه‌ای را بخواهیم، باید از توزیع پواسون با λ = 10×4 = 40 استفاده کنیم.

تابع فوق به عنوان تابعی از k یک تابع جرم احتمال ست. توزیع پواسون می‌تواند به عنوان تقریبی از توزیع دوجمله‌ای در نظر گرفته شود. توزیع پواسون می‌تواند برای سیستم‌هایی بکار برده شود که دارای تعداد وقایع بسیار زیاد هستند و احتمال وقوع هر واقعه بسیار کم است؛ به عنوان یک مثال کلاسیک برای این حالت می‌توان فروپاشی هسته‌ای اتم‌ها را در نظر گرفت (احتمال فروپاشی یک اتم بسیار کم است ولی میلیون‌ها اتم در کنار یکدیگر وجود دارند که در واقع تعداد وقایع بسیاری داریم).

نویز پواسون

پارامتر λنه تنها بمعنی متوسط تعداد وقایع ${\displaystyle E[k]}$ بلکه نشاندهنده واریانس آن نیز می‌باشد${\displaystyle \sigma _{k}^{2}=E[k^{2}]-E[k]^{2}}$ (جدول را ببینید). بنابراین تعداد ظهورهای مشاهده شده حول مقدار متوسطش λ با انحراف معیار ${\displaystyle \sigma _{k}={\sqrt {\lambda }}}$. این نوسانات با عنوان نویز پواسون یا (معمولاً در الکترونیک) به عنوان shot noise شناخته می‌شوند. ارتباط میانگین و انحراف معیار در شمردن ظهورهای گسسته به‌طور علمی مفید است. با دقت کردن به اینکه چگونه نوسانات با مقدار متوسط سیگنال تغییر می‌کنند می‌توان سهم هر سیگنال را تخمین زد، حتی اگر این سهم بقدری ضعیف باشد که نتوانیم به‌طور مستقیم آن را آشکار کنیم.

توزیع‌های مرتبط

• اگر ${\displaystyle X_{1}}$ توزیع پواسون با پارامتر ${\displaystyle \lambda _{1}}$ و ${\displaystyle X_{2}}$ توزیع پواسون با پارامتر ${\displaystyle \lambda _{2}}$ داشته باشد آنگاه تفاضل آن‌ها دارای توزیع skellam خواهد بود.
• اگر ${\displaystyle X_{1}}$ با توزیع پواسون با پارامتر ${\displaystyle \lambda _{1}}$ و ${\displaystyle X_{2}}$ با توزیع پواسون با پارامتر${\displaystyle \lambda _{2}}$ مستقل باشند و ${\displaystyle Y=X_{1}+X_{2}}$ آنگاه متغیر تصادفی ${\displaystyle X_{1}}$ به شرط ${\displaystyle Y=y}$ دارای توزیع دوجمله‌ای خواهد بود. به‌طور خاص ${\displaystyle X_{1}|(Y=y)\sim \mathrm {Binom} (y,\lambda _{1}/(\lambda _{1}+\lambda _{2}))\,}$ در حالت کلی اگر X₁, X₂,... , X_n متغیرهای مستقل پواسون با پارامترهای λ₁, λ₂,... , λ_n باشند آنگاه :: ${\displaystyle X_{i}\left|\sum _{j=1}^{n}X_{j}\right.\sim \mathrm {Binom} \left(\sum _{j=1}^{n}X_{j},{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)}$[1]

خواص

میانگین و واریانس توزیع پوسان هر دو برابر است با ${\displaystyle \lambda }$

امید ریاضی قدر مطلق انحراف از میانگین متغیر تصادفی ${\displaystyle X}$ که از یک توزیع پوسان پیروی می‌کند برابر است با ${\displaystyle \operatorname {E} |X-\lambda |=2\exp(-\lambda ){\frac {\lambda ^{\lfloor \lambda \rfloor +1}}{\lfloor \lambda \rfloor$ !}}}

مد توزیع احتمال پوسان برابر است با ${\displaystyle \scriptstyle \lfloor \lambda \rfloor }$

منابع

1. en:Poisson distribution